Разработка модели канала с релеевскими замираниями для системы HSDPA

Одной из основных проблем в задачах анализа беспроводных сотовых сетей связи является разработка модели физического уровня передачи с учетом таких явлений, как многолучевое распространение и эффект Доплера. В статье эта проблема рассматривается применительно к сотовым сетям третьего поколения, в частности к системам, базирующимся на технологии HSDPa (High-Speed Downlink Packet Access, высокоскоростной пакетный доступ по нисходящему каналу), принятой в стандарте UMTS [1]. Модель канала должна отражать текущие значения отношения сигнал/шум (с/ш), которые используются приемником для того, чтобы информировать передатчик о выборе оптимальной схемы модуляции и кодирования, с тем чтобы минимизировать вероятность ошибки. Предложена модель отношения с/ш, полученная на базе дискретных марковских цепей, которая затем используется для вычисления вероятности ошибок кадров.

Моделирование беспроводного канала связи

На рис. 1 представлена обобщенная схема беспроводной системы связи. В базовой станции на передающей стороне установлен контроллер адаптивноймодуляции и кодирования. В абонентском терминале на приемной стороне установлен селектор адаптивной модуляции и кодирования. Селектор, основываясь на текущем отношении с/ш, выбирает комбинацию схем модуляции и кодирования и передает служебную информацию по обратному каналу контроллеру.

Обратный канал связи

Рис. 1. Модель беспроводной системы связи

Задачей контроллера адаптивной модуляции и кодирования является гарантирование приемлемой вероятности ошибки путем подстройки параметров передачи под текущее состояние канала.

Модель отношения сигнал/шум на временной оси. Основной проблемой в задачах анализа беспроводных сетей является разработка модели физического уровня передачи. Необходимо создать модель изменений качества канала (отношение сигнал/шум – с/ш) и связанной с этим изменением вероятности ошибки. В общем случае распределение отношения с/ш на приемной стороне в канале с релеевскими замираниями подчиняется экспоненциальному распределению с следующей плотностью распределения вероятности:

P ( Y ) = — exp l--

^γ 0      ⎝ ^γ 0 ⎠

где ^γ 0 – среднее значение и ^γ – мгновенное значение отношения с/ш на приемной стороне.

Однако это описание не зависит от времени. Для того чтобы получить отношение с/ш на временной оси, воспользуемся аппаратом цепей Маркова. На рис. 2 представлен образец отношения с/ш на временной оси на приемной стороне. Разобьем диапазон значений с/ш на n уровней. Тогда значения с/ш, попадающие в интервал между каждыми двумя следующими уровнями, будут соответствовать одному из состояний цепи Маркова [2].

Скорость изменения значений отношения с/ш на приемной стороне зависит от максимальной частоты Доплера f m ^. Частота пересечения уровней определяется как число пересечений замирающим сигналом данного уровня в единицу времени.

τk

.

N (Гк) + N (Гк+1)

Плотность распределения вероятности длительности пребывания t в одном из состояний цепи Маркова подчиняется экспоненциальному распределению с параметром τ_k . Плотность распределения для экспоненциального закона может быть выражена как

f(t) = тк ехр(-тkх).            (5)

Подставляя (3) и (2) в (4), получаем выражение для средней длительности пребывания в каком-либо состоянии:

ехр

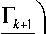
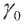
С/Ш-состояние цепи Маркова

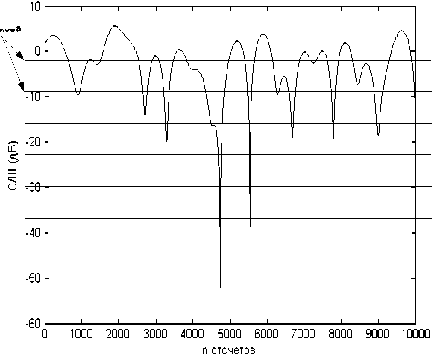
Рис. 2. Разбиение отношения с/ш на уровни в реле- евском канале

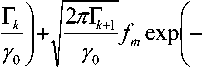
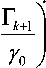
Вероятности перехода из одного состояния в другое определяются следующим образом [2]:

Pk,k+1 “ N(Гк“)Tp ,к = 0,1--K -1,  (7)

π _k

_ N(Г)тpPk,k-1 ~              ’ k 1,2,"",K 1 ,     (8)

где T _p – длительность кадра, который является элементом передачи в стандарте HSDPa.

Выбор численных параметров цепи Маркова и результаты имитационного моделирования

Частота пересечения в любую сторону любого уровня, попадающего в область значений с/ш на приемной стороне, определяется выражением вида [2]

N (Г) =

2п Г---f m exP

/

-

⎝

Γ⎞

γ0⎠

Вероятность π k пребывания в каком-либо из состояний определяется следующим образом [2]:

Для определения параметров цепи Маркова необходимо выбрать значения длительности кадра T _p и максимальной частоты Доплера ^f m ^. В стандарте HSDPA длительность кадра T _p составляет 2 мс. Максимальная частота Доплера f _m определяется выражением (9), где f _c – несущая частота стандарта HSDPa (2,1 ГГц), v – скорость мобильного пользователя (в данной работе принята 5 м/с) и c – скорость света:

Гк +1

πk

∫

Гк

p(γ )dγ = exp

⎛ ⎜⎜-⎝

Γ⎞    ⎛

k ⎟-exp⎜

γ0⎠       ⎝

Г к+1

γ0

⎟⎟. (3)

⎠

v

m c, c fm = 1-39m / s • 2.1 -109Hz = 9.66Hz .

m 3-10 8 m / s

Средняя длительность пребывания в каком-либо состоянии цепи Маркова представлена в следующей форме [2]:

Селектор адаптивной модуляции и кодирования определяет, какой формат передачи (комбинация схем кодирования и модуляции) будет оптимальным для текущего качества канала. Целью селекто-

ра является выбор такого формата,который обеспечивал бы вероятность потери кадров P ₀ не более 10% [1]. Выбор селектора передается контроллеру по обратному каналу в форме параметра качества канала (Channel Quality Indicator – CQI), принимающего значения от 0 до 30. Контроллер на передающей стороне применяет выбранный формат для передачи в течение одного (или более кадров).

Очевидно, что целесообразно связать состояния цепи Маркова с возможными форматами передачи. Для этого необходимо найти зависимости вероятности ошибки кадров (Frame Error r ate – fEr) от отношения с/ш. В стандарте HSDPa возможны две схемы модуляции – QPSK и 16-QAM.В качестве схемы кодирования используется турбокод 1/3. При помощи операций с битами (повторение, прокалывание), описанными в стандарте [3], можно получить до 31 формата передачи, использующих виды модуляции QPSK либо 16-QAM и переменное отношение информационных и кодовых бит. Параметры этих форматов приведены в таблице 1.

В данной работе вероятность ошибки кадра, fEr, была получена путем имитационного моделирования для 15 форматов передачи в соответствии со стандартом [4] (c 4-го по 18-й формат). Для моделирования использовался пакет MaTLab и дополнительный пакет для моделирования процессов турбокодирования/декодирования [5].

Зависимости на рис. 3-7 получены для отношения с/ш в одном канале передачи. Для случая нескольких ортогональных каналов передачи значение с/ш, соответствующее вероятности ошибки fEr, должно быть рассчитано по формуле:

SNR=Es I No+10log(n), (10)

где Es / No – отношение с/ш для одного канала передачи, n – число используемых ортогональных каналов передачи. Далее, исходя из полученных зависимостей, целесообразно определить отношения с/ш,соответствующие вероятности P 0 = 10%, и использовать эти значения с/ш в качестве дискретных уровней Г _к , Г _{к + 1} цепи Маркова.

Таблица 1. Форматы передачи в стандарте HSPDa

Зна че-ние CQI	Число инфор-маци-онных бит	Число ортогональных каналов передачи	Тип модуляции	Отношение ин-формационных и кодовых бит
4	317	1	QPSK	0.344
5	377	1	QPSK	0.409
6	461	1	QPSK	0.501
7	650	2	QPSK	0.353
8	792	2	QPSK	0.430
9	931	2	QPSK	0.505
10	1262	3	QPSK	0.457
11	1483	3	QPSK	0.537
12	1742	3	QPSK	0.631
13	2279	4	QPSK	0.619
14	2583	4	QPSK	0.701
15	3319	5	QPSK	0.721
16	3565	5	16-QAM	0.371
17	4189	5	16-QAM	0.436
18	4664	5	16-QAM	0.485

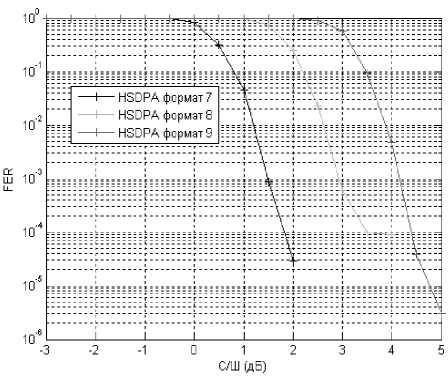
Рис. 4. Зависимости вероятности ошибки кадров от отношения С/Ш (форматы 7–9)

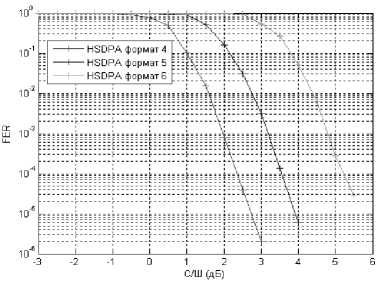
Рис. 3. Зависимости вероятности ошибки кадров от отношения с/ш (форматы 4–6)

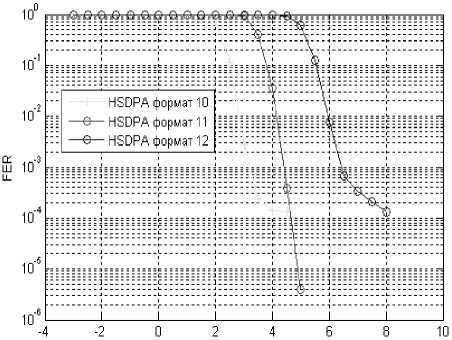
С/Ш (дБ)

Рис. 5. Зависимости вероятности ошибки кадров от отношения с/ш (форматы 10–12)

В результате имитационного моделирования был получен набор значений fEr (координаты точек на оси ординат); им соответствуют значения с/ш (координаты точек на оси абсцисс), используемые в качестве входных данных для имитационного моделирования в диапазоне от – 4 дБ до 6 дБ с шагом 1 дБ.

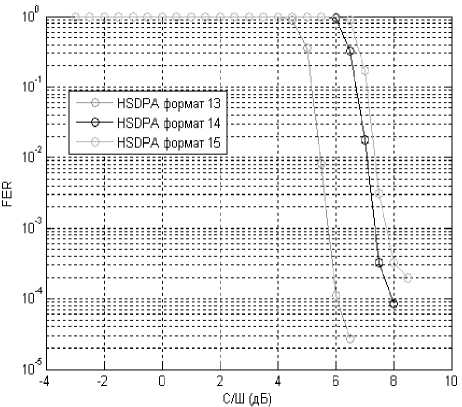
Рис. 6. Зависимости вероятности ошибки кадров от отношения С/Ш (форматы 13–15)

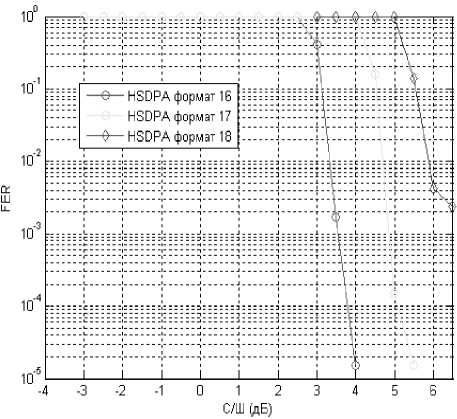
Рис. 7. Зависимости вероятности ошибки кадров от отношения с/ш (форматы 16–18)

Значения с/ш, соответствующие вероятности потери кадра P0 =10%, были рассчитаны с помощью линейной интерполяции. Для этого воспользуемся значениями вероятности ошибки ( У0, У1), являющимися такими, что точка с координатами P0 =10% попадает в интервал ( y0, у1). Значения с/ш (значения на оси абсцисс с координатами (x0, Х1)) известны из входных данных имитационного моделирования. Тогда а = y - yo , У1 - У о x = x0 + а ■ (x1 - x0).

Например, для формата 8 находим:

0.1 - 0.45 а =

0.03 - 0.45

= 0.99 ,

x = 2 + 0.99 ■ (2.5 - 2) = 2.495 дБ.

С учетом двух ортогональных каналов передачи необходимо воспользоваться (10):

с/ш = x + 10log(2) = 5.41 дБ.

Полученные значения отношения с/ш, соответствующие вероятности потери кадров P ₀ не более 10%, приведены в таблице 2.

Таблица 2. Значения отношения с/ш при P0 ≤ 10%

Значение CQI	Отношение с/ш, соответствующее вероятности P 0 =10% (дБ)
4	1
5	2.43
6	3.95
7	4.57
8	5.41
9	6.51
10	7.27
11	8.72
12	10.27
13	11.4
14	12.94
15	14.29
16	15.3
17	16.7
18	17.6

С помощью (2)-(8) были получены значения средней длительности состояния τ k и вероятности перехода P k , _{k + 1} , P k , k _{- 1} из одного состояния S k цепи Маркова в другое. Эти данные приведены в таблице 3.

Затем в соответствии с полученными данными было проведено имитационное моделирование канала с релеевскими замираниями. В результате имитационного моделирования было получено 105 значений с/ш. На рис. 8 представлены значения с/ш в диапазоне значений отсчетов от 35×103 до 39×103. На рис. 9 представлены значения с/ш в диапазоне значений отсчетов от 60×103 до 65×103.

Таблица 3. Параметры цепи Маркова

Sk	Γ k , Γ k+1 (дБ)	τ k (s) (с)	P k, k + 1	P k , k - 1
0	–inf..1	0.093	1	0
1	1..2.43	8.294Е-3	0.312	0.688
2	2.43..3.95	0.01	0.415	0.585
3	3.95..4.57	4.79E-3	0.332	0.668
4	4.57..5.41	6.984E-3	0.394	0.606
5	5.41..6.51	9.894E-3	0.475	0.525
6	6.51..7.27	7.671E-3	0.479	0.521
7	7.27..8.72	0.014	0.249	0.751
8	8.72..10.27	0.014	0.18	0.82
9	10.27..11.4	0.012	0.205	0.795
10	11.4..12.94	0.011	0.183	0.817
11	12.94..14.29	9.294E-3	0.216	0.784
12	14.29..15.3	7.955E-3	0.252	0.748
13	15.3..16.7	7.095E-3	0.282	0.718
14	16.7..17.6	6.038E-3	0.331	0.669
15	17.6..+inf	5.444E-3	0	1

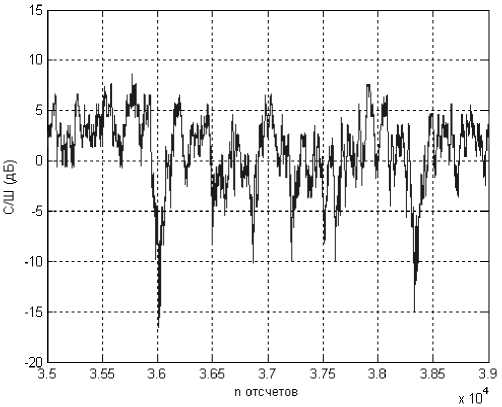
Рис. 8. Моделирование канала с релеевскими замираниями (1)

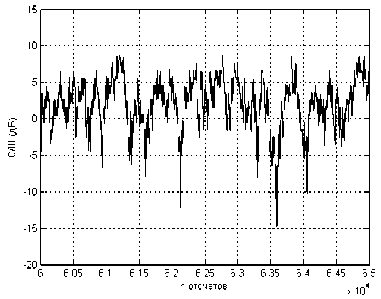
Рис. 9. Моделирование канала с релеевскими замираниями (2)

Заключение

В данной работе представлена модель канала ре-леевских замираний в форме дискретной цепи Маркова с конечным числом состояний. На базе данных, полученных из материалов стандарта HSPDa, были определены численные значения соответствующих параметровдляимитационногомоделированиякана-ла HSDPa.В дальнейшем планируется использовать данную модель канала для расчета характеристик качества обслуживания в сетях беспроводной связи, в том числе для получения таких характеристик, как средняя задержка и джиттер канала HSPDa.