Разработка модели определения фактора трения для пятиклетевого стана непрерывной горячей прокатки 2800

Современные горячекатаные заготовки из алюминиевых сплавов, помимо определенных уровней физико-механических свойств и качества поверхности, также должны соответствовать строгим требованиям по геометрическим характеристикам [1]. Так, для обеспечения требований технических условий, допустимые пределы разнотолщинности на горячекатаной заготовке устанавливаются на уровне ±0,25 мм [2]. Но для баночной ленты отклонения устанавливаются на порядок ниже. Это происходит из-за высокоскоростных условий штамповки банок, наличие такой разнотолщин-ности приводит к критическому росту силы трения, вызывающей отказы оборудования. В связи с этим допустимое отклонение толщины баночной ленты регламентируется диапазоном ±0,005 мм, а горячей заготовки ±0,025 мм. Обеспечение требуемой разнотолщинности является одной из ключевых задач прокатного производства [3-4]. На сегодняшний день остаётся нерешённой проблема утолщённых концов катаной продукции, длина которых значительно влияет на коэффициент выхода готовой продукции. Одной из причин отклонения по толщине является неточное определение величины упругого растяжения клети, возникающего вследствие действия сил в очаге деформации [5-6]. Чтобы компенсировать упругие деформации, зазоры устанавливают с учётом расчётной поправки, величина которой определяется математической моделью стана. Точность данной модели непосредственно влияет на продолжительность периода достижения заданной толщины проката и, следовательно, длину участка полосы с отклонением от допустимых значений толщины заготовки.

Современные расчетные модели горячей прокатки базируются на уравнении Кармана-Целикова, [7] одним из параметров адаптации, в котором является коэффициент или фактор трения (далее показатель) в зависимости от выбранного закона определения контактных касательных напряжений.

Так для прокатки алюминиевых сплавах в непрерывных станах горячей прокатки в основном применяется модель Зибеля [8]:

,                                                          (1)

,                                                       (2)

где – фактор трения;

• и   – предел текучести деформируемого материала при растяжении и сдвиге соответственно;

Д ^ – абсолютные обжатия;

• и   – коэффициенты, подбираемые эмпирически.

Адаптация модели осуществляется обратным пересчетом, основываясь на фактически замеренных параметрах прокатки (толщина, скорость, натяжение, опережение и усилие прокатки). Длительность такого расчета зависит от того, насколько точно задан показатель трения для первой итерации.

Таким образом несмотря на то, что показатель трения является параметром адаптации, определение его является важным аспектом для оптимизации процесса обработки металлов давлением и напрямую влияет на выход годного при прокатки алюминиевых сплавов [9].

Основной недостаток данной модели, вызван тем, что ряд условий прокатки, влияющих на фактор трения m, а именно, вязкость смазки (в зависимости от давления), скорость, прокатки, длина очага деформации в первой и последней клети сильно отличаются. При это данные переменные не учитываются в выражении (2). Поэтому использование уравнения (2) при настройке регулирующих воздействий приводит либо к завышенной ошибке в расчетах усилия на первой клети, или на последней. В результате чего автоматическое регулирование становится невозможным и процесс настройки стана осуществляется оператором в ручном режиме, что приводит к неоправданно большой длине настроечного участка, на котором разнотолщинность выходит за допустимые требования [10-11].

Целью данной работы является повышение точности модели расчета контактных напряжений при прокатке в многоклетьевых станах за счет учета влияния скорости прокатки, длины очага деформации и вязкости смазки.

МЕТОДИКА ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА

Испытания проводились на линии горячей прокатки АО СМЗ . Стан производит рулоны и плиты из алюминиевых сплавов, толщиной от 2,2 мм до 60 мм, шириной от 1100 мм до 2150 мм, массой рулона до 20 т.

В состав линии горячей прокатки входит реверсивная клеть черновой прокатки, пятиклетевая непрерывная группа и подпольная моталка для смотки полосы в рулон. Прокатные клети типа квар-то. Технические характеристики стана представлены в таблице 1.

Таблица 1 – Технические характеристики клетей непрерывной группы стана горячей прокатки

Наименование параметра	Величина параметра
Диаметр рабочих валков, мм	650 ÷630
Диаметр опорных валков, мм	1400 ÷1350
Длина бочки рабочих и опорных валков, мм	2800
Максимальная ширина прокатываемой горячекатаной полосы, мм	2300
Максимально допустимое усилие при прокате, Н*10 6	24,5
Максимальная скорость прокатки в клети, м/мин
F1	72
F2	90
F3	134,4
F4	270
F5	324
Номинальная мощность двигателя каждой клети, кВт	4200

Во время прокатки система измерения регистрирует следующие параметры: обжатия (датчиками положения), температуру раската и полосы на выходе из клети F5, усилие прокатки (месдозы под подушками опорных валков), межклетевые натяжения (месдозы в роликах натяжения), толщи- ну полосы и ее профиль (рентгеновские толщиномер и профилемер), скорость полосы и вращения рабочих валков (тахометры на роликах натяжения и на рабочих валках).

Для построения физической модели связи пиковых напряжений и скоростей деформации исполь зуем закон, предложенный Селларсом, который часто применяется для алюминиевых сплавов [12-14]:

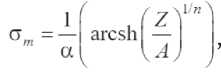
где A , a , n - константы исследуемого материала, подлежащие определению из данных экспериментов регрессионным анализом;

Z - это параметр Зенера-Холломона, который описывает деформационное поведение металлических материалов:

4 = ^^■' — '.

К 2

В выражении (4) -■ и T - соответственно скорость (с^-1) и абсолютная температура (К) деформации; R - газовая постоянная (Дж/моль.К); Q - энергия активации (Дж/моль) процесса, контролирующего горячую деформацию; -J-:. - максимальное напряжение текучести

РЕЗУЛЬТАТЫ

Для решения данной задачи определялась аналитическая зависимость контактных касательных напряжений от параметров прокатки. Для этого в свою очередь был проведен статистический ана- лиз данных, полученных при прокатки алюминиевых полос и лент на непрерывном стане пятиклетевом стане горячей прокатки 2800. Для каждой катаной полосы численным методом (Эйлера) определялось значение фактора трения m, обеспечивающего требуемый уровень сходства между измеренными значениями опережения и усилия прокатки с фактическими. Влияние основных переменных на фактор трения представлены на рисунке 1.

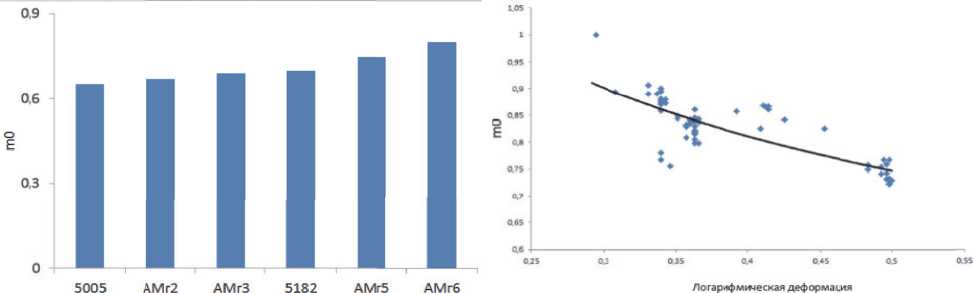
(а)                                       (б)

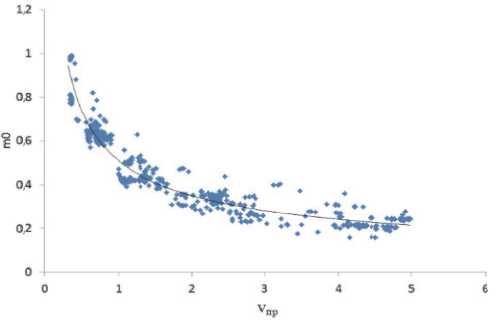
(в)

Рисунок 1 - Влияние основных факторов на фактор трения: а) от сплава; б) от обжатия; в) от скорости прокатки

Анализ статистических данных позволил вывести функцию для расчета фактора трения в зависимости от вязкости масляной фазы эмульсии ■■(, скорости прокатки ; ■, предела текучести -S_: и длины проекции дуги захвата на направление прокатки ■ ,■:

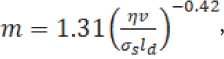
Данная зависимость графически представлена на рисунке 2.

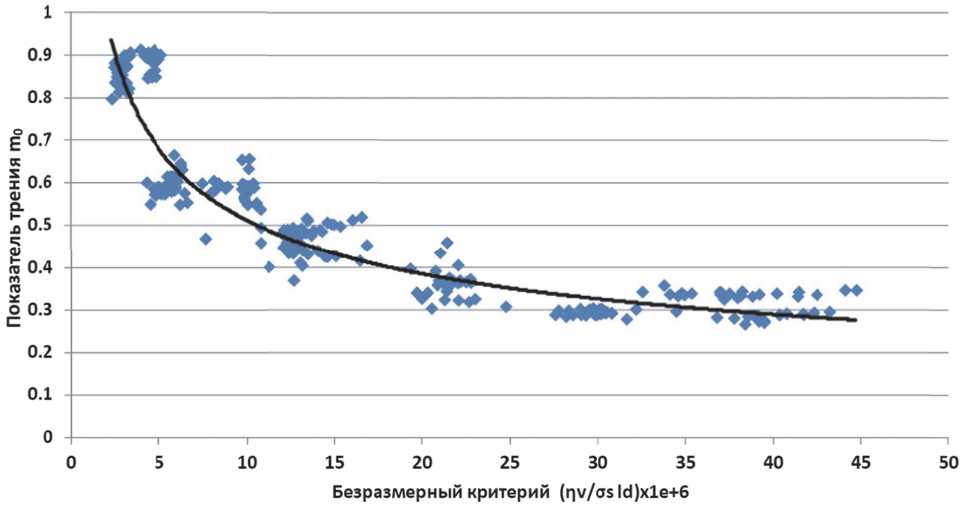
Рисунок 2 – Зависимость фактора трения от безразмерного критерия

Тогда уравнение контактных касательных напряжений принимает вид z ч 0.42

τ= O.75P)   a/42,

^^

Коэффициент корреляции при использовании данного выражения составляет 0.93 (рисунок 3), что говорит о его адекватности, но стандартное отклонение равно 0.064, что приводит к отклонению в расчете усилия в пределах -200..+200 тонн силы.

35 000

30 000 ш

x ф 25 000 s

£ 20 000

ф g 15 000 o

т t 10 000

TO

e

5 ooo

5 000   10 000  15 000  20 000  25 000  30 000  35 000

Расчетные значения, кН

Рисунок 3 – Сравнение расчетных значений усилия прокатки по модели с фактическими измеренными на стане

Отклонения объясняются состоянием поверхности валков, вариацией характеристик эмульсии, точностью измерений параметров прокатки [15].

Функция (4) интегрирована в автоматическую систему управления стана. В результате внесенных изменений повышена точность расчетов режимов прокатки и значительно увеличена скорость адаптации системы. Длина дефектного конца рулона, на котором происходит настройка стана на требуемую толщину, сократилась с 80–100 м до 20–30 м (рисунок 4), что обеспечило увеличение выхода годного на 2%.

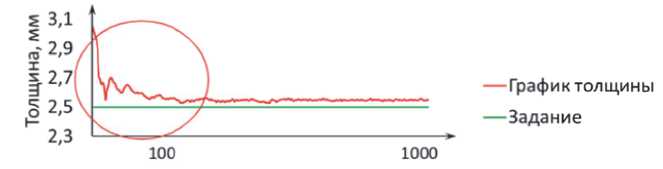
(a)

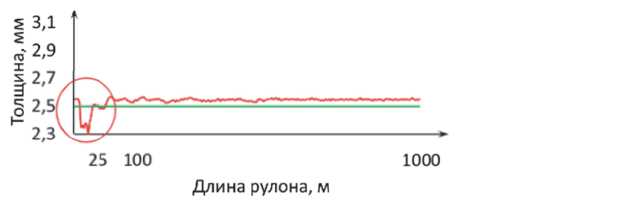
— Графи к толщины

—Задание

• (б)

Рисунок 4 – График выхода толщины полосы на заданную: а) со старой моделью на основе формулы (2); б) по новой модели – уравнение (6)

ВЫВОДЫ

Разработана модель для расчета контактных касательных напряжений в зависимости от таких параметров прокатки, как вязкость масляной фазы эмульсии, скорость прокатки, предел текучести при температуре прокатки и длина проекции дуги захвата на направление прокатки. Модель основана на законе Зибеля с определением фактора трения по формуле (5). Внедрение разработанной модели позволяет автоматизировать процесс выхода на годную толщину и при этом значительно сократить области с отклонениями по толщине.