Разработка модели прогнозирования временных рядов нестационарных дискретных систем на основе нейронной сети

Актуальность темы. Нестационарным процессам, отражающим технологические, экономические, социальные, биологические, физические явления свойственны количественные и качественные характеристики, которым присущи скачкообразное, эволюционирующее развитие и регулирование параметров с течением времени. Наиболее подходящим механизмом описания таких процессов при формализации являются динамические случайные временные ряды, позволяющие применять методы адаптивного моделирования с целью выработки методов и алгоритмов регулирования описательных параметров [1]. Важным моментом при этом является то, что для достижения адаптивности моделей необходимо использование прогнозирующих функций, способных выдавать значения требуемых показателей на основе предшествующих членов временного ряда [2].

Моделирование нестационарных процессов в общем случае может осуществляться с помощью традиционных математических методов, однако на сегодняшний день перспективным направлением исследований является применение современных методов интеллектуальной обработки данных, одним из ярких представителей которых считаются нейросетевые технологии [3].

Теоретический и практический опыт традиционных методов прогнозирования развивается на базе фундаментальных концепций и принципов управленческого финансирования. При этом, помимо получения возможных будущих оценок тех или иных исследуемых параметров, целью прогнозирования также является определение возможных событий во внешней и внутренней среде и последствий для экономики.

Проблема прогнозирования процессов вследствие быстрых, порой плохо предсказуемых изменений внешней среды, в последние годы стала особенно сложной. С учетом этих

• (с) А. Р. Ахатов, Ф. М. Назаров, 2018

трудностей и критичности ошибок в прогнозах некоторые специалисты были вынуждены заговорить о тщетности прогнозирования нестационарных процессов и сложности структурных характеристик систем экономики [4, 5].

Проблемам анализа и прогнозирования нестационарных процессов в экономической литературе уделено недостаточное внимание. Несколько публикаций посвящено общим теоретическим вопросам о роли этих инструментов. Ведутся дискуссии о преимуществах систематизации анализа и прогнозирования, но единого аппарата исследования нестационарно-эволюционных процессов пока не существует. Остается неосвещенным ряд актуальных вопросов, например, способы определения характеристик процесса, механизм изучения структуры объекта, анализа факторов, выбор методов прогнозирования, повышение эффективности прогнозов.

В связи с этим, можно констатировать, что актуальным направлением исследования является разработка методов и механизмов осуществления идентификации типа и прогнозирования значений процессов и характеристик их поведения с использованием новейших технологий.

В настоящем исследовании рассматриваются вопросы моделирования нестационарных дискретных систем, описывающих процессы, подобные оплате образовательных контрактов, расходу электроэнергии, продаже скоропортящихся товаров, которые осуществляются в условиях временных ограничений и запаздывания, с целью построения систем мониторинга оплаты образовательных контрактов, прогноза и планирования показателей снабжения электроэнергии, планирования объемов скоропортящихся товаров, приобретаемых для розничной торговли, в которых реализуются функции контроля достоверности, сглаживания, регулирования факторов, приводящих к невыполнению назначенных объемов и сроков.

Описание нестационарных дискретных систем на основе уравнений управления обратной связью по состоянию. В нестационарных дискретных системах для отражения условий ограничения и запаздывания подходящим механизмом могут оказаться уравнения терминального управления обратной связью по состоянию.

Анализ литературы показывает, что для некоторых классов нестационарных систем решения задач терминального управления получены на основе синтеза решений для линейных стационарных систем [6].

В работах [6, 7] приводятся достаточные условия существования и явный вид терминального управления обратной связью по состоянию для линейных нестационарных дискретных систем.

И сходя из теоретических положений и аналитических результатов работ [2, 6], нами предложена модель нестационарной дискретной системы в условиях ограничений и запаздывания. Для начала представим дискретную стационарную линейную систему управления, описываемую уравнениями

X k +i = Ax k + bu k ; xo; X k E R n k = 0,1..., (1)

где переменные A и b считаются заданными.

При введении переменной ^ — фактора влияний внутренних и внешних возмущений — скалярное управление обратной связью по состоянию описывается выражением

U k = V • X k , (2)

при котором для решения замкнутой системы

X k +i = Dx k ,     D = A + by,                         (3)

и заданных m, m >  n,r выполняется условие

X m = Г,                                         (4)

где r — пороговое значение. которое достигается за m шагов.

Если a i (i = 0,1 ...n) — коэффициенты характеристплоского многочлена, матрицы A. то матрицу y можно представить в следующем виде:

	1 α 1	0          .. 1             ..	. 0 . 0	0 0		1 α 1	0          .. 1             ..	. 0 . 0	0 0
y =		. .			, y =		. .
	an-	. 1 α n - 2     .	. . α 1	1		an-	. 1 α n - 2    .	. . α 1	1

Перейдем теперь к определению условий существования и явного вида, скалярного управления для нестационарной системы. Вид выражения скалярного управления нестационарной системы принимает вид

U k = y k X k , (5)

где yk,(k = 0,1,...,l) — факторы влияний внутренних и внешних возмущений при локальных коэффициентах /-го сегмента, нестационарного ряда, при которых для решения замкнутой системы xk+1 Dkxk, Dk Ak + bkyk (6)

и заданных m, r выполняется условие (4).

Решения систем (6) определяют условия существования и явный вид вектора обратной связи, обеспечивающего переход системы в заданное состояние за заданное число шагов m,m 6 n.

Однако, ввиду нестационарности исследуемых процессов, уравнения, определяющие спектр матрицы преобразования системы, согласно результатам, приведенным в [7], решаются неоднозначно, а это приводит к требованию оптимизации поставленной задачи управления нестационарными процессами, например за счет анализа, прогнозирования и регулирования параметров возмущающих факторов.

Прогнозирование нестационарных экономических процессов по методу адаптивного статистического прогнозирования. На практике для регулирования возмущений временных рядов с варьирующими характеристиками наиболее часто используется метод экспоненциального сглаживания [8]. Этот метод является одним из методов адаптивного прогнозирования и приспособлен для количественной оценки влияния, которое оказывают на прогнозируемый показатель предшествующие члены динамического ряда с учетом их отдаленности от конца, рассматриваемой последовательности переменных величин [9]. При использовании метода, экспоненциального сглаживания степень воздействия каждого члена динамического ряда на величину переменной y k ,(k = 0,1,...,l) распределяется в соответствии с экспоненциальным законом.

Отличительной особенностью адаптивных методов прогнозирования является неоднозначный подход к элементам ряда, расположенным в начале, середине и конце последовательности числовых величин. Это позволяет отразить тот факт, что воздействие замыкающих наблюдений отражается на прогнозных оценках более заметно, чем влияние начальных уровней ряда.

Пусть тенденция изменения параметра возмущений описана в виде полинома [7]:

W = а + а • t + -^ • t² + -33 • t³ +-----и pp! • t p .                     (7)

Для того чтобы регулирование параметров на основе модели (7) приводило к адаптации, принято использование вычислительной схемы, которая корректирует параметры уравнения после очередного периода времени для исследуемого сегмента.

Разработана методика, которая позволяет выразить на основе модели (7) совокупность экспоненциальных средних первого ( S1), второго (S_t²), ..., к-го (S^) порядка для осуществления процедур регулирования параметров vk- Расчет экспоненциальных средних осуществляется по формулам:

n

S t = a X⁽¹ - ^a)j • V t ;

j=0

n

S t = а X (1 - a)^j • St¹;

j=0

n

St = а X (1 - a)j • Sk-1 , j=a где a — коэффициент уровня прогнозирования для параметра сглаживания.

Выбор значения коэффициента параметра сглаживания а влияет на отражение тенденции изменения показателя, характеризующего запаздывание в зависимости от ограничения. При малых а достоверность прогнозируемого уровня низка, так как резкое уменьшение значения регулируемого параметра приводит к еще большим возмущениям в тренде динамического ряда. При больших а достоверность прогнозируемого уровня высока, так как значение параметра регулирования будет постепенно сглаживать тенденцию замыкающих элементов рассматриваемой совокупности. То есть чем больше величина параметра сглаживания, тем модель лучше способна адаптировать регулируемые параметры, а именно увеличить или уменьшить ограничение для сглаживания запаздывания.

Такое свойство адаптивности модели (7) определяет подход к выбору константного значения параметра сглаживания в зависимости от типа прогноза. При краткосрочных прогнозах принятие значений а на относительно высоком уровне позволит учитывать и анализировать оперативную информацию для прогнозирования состояния объекта в зависимости от недалекого прошлого. Уменьшение значения константной переменной по мере увеличения глубины прогноза делает модель способной учитывать перспективность формирования сглаживающей переменной vt-

Отметим, что значение параметра сглаживания возможно определять на различных видах полинома, например, линейном и параболическом [6]:

V t ^— «о + ^а1 • t,

V t ^— «о + ^а1 • t + 2 • t².

При этом, увеличение размерности полинома не обязательно улучшает точность сглаживающего параметра, а это значит, что необходимо дополнительное исследование для оценки точности регулируемого параметра, при котором достигается минимальная ошибка прогноза [7].

Выберем значение коэффициента сглаживающего параметра при длине интервала сглаживания т, приблизительно равной продолжительности длины ряда с учетом как минимум двух сегментов временного ряда, т. е.

a —----7

m + 1

.

Разработанный алгоритм определения и оценки точности сглаживающего параметра состоит из следующих шагов.

• 1)    Инициализация значений коэффициентов уравнений описания параметра сглаживания при уравнениях (9) и (10).

• 2)    Определение начальных значений экспоненциальных средних по формулам

с 1 _ —  ¹ - a —

S1 — «о--ао,

a

С2 -- ² - a --

S1 — « 1-- « 1 .

1 a

Q1         1 -	a      (1 -	a) • (2 -	a)
S1 — «о a
	«1 |	2a2	• «2;
С 2_     2(1 -	a)       (1	- a) • (3 -	- 2a)
S1 — «0	«1 1		• «2;
a		a2
с3_     3(1 -	a)      3(1	- a) • (1	- 3a)
S1 — a0 - a	«1 1	2a2	· α2

• 4)    Нахождение параметров прогнозирующей функции:

  а — 2S 1 - S 2

  
  

  «1 —

  
  

  a

  
  
  
  

  _-

  
  

  a

  
  
  

  _-

  
  
  
  

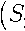
  S 2²

  
  
  
  

Для параболической модели «0 , « 1 , a2 — находятся по формулам:

«0 — 3 (S21 - S22) + S22

«Г — a • (1 - a)² • [(6 - 5a) • S t ¹ - 2(5 - 4a) • S_t² + (4 - 3a) • S_t³] «2 ^— 2 • ^{(1 - a)2} • (S t ^{- 2} • S t ² + S3).

• 5)    Установление прогнозного значения переменной для момента времени t + 1:

‘ t +i = ^ао + ^а1 • l;                                      (16)

для параболической модели:

‘ t +i = ^ао + ^а1 • ti + "2! • l²,                                  ⁽¹⁷⁾

где l — показатель периода для краткосрочного, среднесрочного, долгосрочного или другого типа прогноза (l = 1, 2,...).

• 6)    Расчет экспоненциальных средних для t = 2,..., n по формулам:

S t = a • ‘ t + ^(l - ^{a )} • S t - i ;

S t = a • S t 1 + ^(l - ^a) • S t - i ;                                   ⁽¹⁸⁾

S3 = a • S t + ^(l - ^a) • St -v

• 7)    Для расчета экспоненциальных средних и параметров прогнозирующей функции,

расчетных значений показателя для всех остальных значений t осуществляется переход к пункту 4 и реализуется цикл, пока t 6 n.

• 8)    Значения t+1 для мод ели при t = n: фиксируются как прогнозное значение.

Конец алгоритма.

В качестве оценки точности прогноза предлагается среднеквадратическое отклонение прогнозного значения, которое рассчитывается по формуле

^ _t+ l = ^ t • pa/(2 — a)³ • [1 + 4(1 — a) + 5(1 — a)² + 2a(4 — 3a) • l + 2a² • l ² ,      (19)

где                                       _____________

- X        •                         (20)

Отметим, что с помощью такой оценки можно рассчитать доверительные интервалы прогноза, так как при предложенном методе вопрос выбора прогнозирующей функции остается открытым ввиду того, что в общем случае параболическая модель эффективней линейной, однако при скачкообразном (ступенчатом) варьировании переменной временного ряда параболическая модель достигает нового уровня за больший промежуток времени по сравнению с линейной.

Приведенный алгоритм реализован в качестве модуля апроксимации и прогнозирования временного ряда, и получены расчетные данные для трех групп выборочных данных, представляющих стационарные периодические (себестоимость произведенной продукции на примере производства консервантов из фруктов и овощей предприятий Самаркандской области, тыс. сум), нестационарные непериодические (средневзвешенная доходность биржевых облигаций Самаркандской области за 2016 г., % годовых) и нестационарные периодические (суммы поступлений контрактной оплаты на расчетный счет Самаркандского государственного университета, млн. сум) процессы.

Однако, как было указано выше, моделирование экономических процессов может осуществляться также и с помощью нейронных сетей [10]. Нейросетевые технологии дают преимущества при решении задач с неполной, зашумленной, искаженной информацией, для которых практически невозможно получить приемлемые решения с помощью статистических методов аналитического выравнивания. Использование моделей нейронных сетей для обработки массивов данных дает значительный выигрыш в быстродействии процесса, а также в достижении адаптивности модели за счет изменения топологии сети при обучении, исходя из требований решаемой задачи [3, 11, 12].

Описание и прогнозирование нестационарных экономических процессов на основе нейросетевых технологий. Основная проблема использования нейросетевых технологий заключается в правильном выборе архитектуры нейронной сети для решения определенной задачи. Аппроксимацию данных, представляемых временным рядом, можно осуществлять с помощью многослойных, радиально-базисных, обобщенно-регрессионных и др. типов сетей [3, 11, 12]. Причем, практика применения нейросетей показывает, что в зависимости от типов задач различные архитектуры сетей выдают разное качество решений. Исходя из результатов анализа научно-технической литературы, в данном исследовании нами принято построение нейросетевой модели экономического процесса с применением каскадной (cascade-forward backpropagation neural network [13]) архитектуры нейронной сети, которая отличается простотой и эффективностью при аппроксимации данных с сохранением приемлемого качества моделирования.

Обучение нейронной сети принято осуществить на основе наиболее популярного и распространенного алгоритма обратного распространения ошибки, т. к. все его характеристики подходят для выбранной архитектуры сети и решения поставленной в исследовании проблемы [10, 13].

Основной целью моделирования является построение прогноза будущего состояния динамического ряда, а для обеспечения высокой точности обработки данных требуется подбор весовых коэффициентов, гарантирующих такую точность. В связи с этим, в качестве параметра сети, который априори привязан к определенному типу входных данных и вариации которого позволяют сделать лучший выбор, определено среднее допустимое отклонение начальных весовых коэффициентов ст.

Для иллюстрации применения нейронной сети при моделировании экономических процессов были взяты те же данные, которые были использованы при реализации модуля аппроксимации и прогнозирования на основе метода адаптивного статистического прогнозирования.

Отметим, что построение прогнозной модели является процессом, продолжающим процедуру моделирования после первичного анализа графического представления исходных данных.

Для определения степени предпочтительности используемого метода при принятом виде данных принято среднее отклонение прогнозного значения на прогнозируемом участке как для адаптивного статистического, так и для нейросетевого метода [7, 13]:

N — k

N

X X i=k+1

CT i

^{— ст} i

CT i

где ст i — оценка, построенная по соответствующему методу.

Согласно этой методике, высокой точности прогноза соответствуют значения у < 0,1; хорошая точность достигается при 0,1 < у < 0,2; удовлетворительная точность — при 0,2 < у < 0,5: исудовлстворитсльпая точность — при у > 0,5.

Для решения задачи прогнозирования, как и в работе [11], применим метод проекции временного ряда. Тогда задача решается с помощью обученной нейронной сети с выполнением так называемой проекции временного ряда, где количество построенных

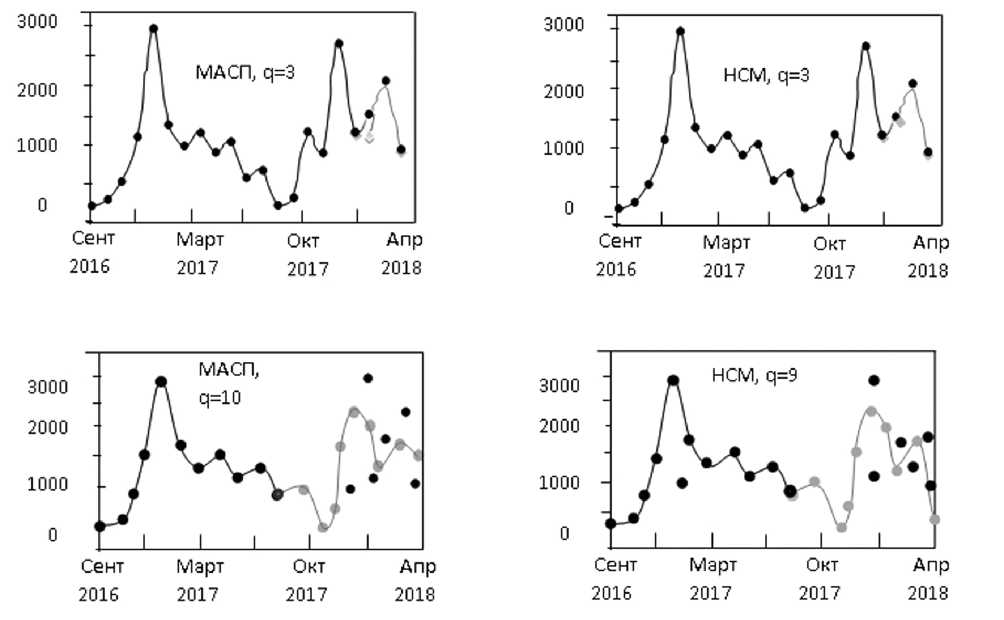
Рис. 1. Расчеты для себестоимости произведенной продукции (тыс. сум)

прогнозных значений называется горизонтом прогнозирования и обозначается символом q, а общий объем ряда динамики обозначается символом N. После обучения сети на выделенных примерах объема (N — q) выдается прогноз следующего значения ряда динамики. Проекция заключается в том, что полученный очередной результат вместе с предыдущей обучающей выборкой снова и снова подается на вход сети, причем это можно повторять произвольное количество раз. Однако увеличение количества повторений не гарантирует улучшения качества прогноза.

Одним из эффективных решений такой проблемы принята организация смены топологии сети в процессе обучения. При использовании каскадной нейронной сети это осуществляется заменой метода минимизации ошибки, в нашем случае, одного из трех методов MSE, RootMSE, Arctan. При определении области топологий нейронных сетей для построения прогнозных моделей произведен анализ качества, а соответственно и адекватности прогноза по коэффициенту среднего отклонения (21).

Результаты экспериментального анализа. Расчеты получены для двух значений горизонта прогнозирования, когда q = 3, q = 9 в соответствии с прогнозом на три месяца и девять месяцев соответственно. После получения результатов применения проекции временного ряда для нейросети при всех трех группах выборочных данных, подсчитаны значения величины y по формуле (21), которая характеризует точность полученного прогноза для обоих исследуемых методов.

На рис. 1-6 проиллюстрированы графики построения прогнозирующих моделей по адаптивному статистическому и нейросетевому методу. На рисунках точки означают исходные данные, линии — график аппроксимирующей функции, прогнозные значения в

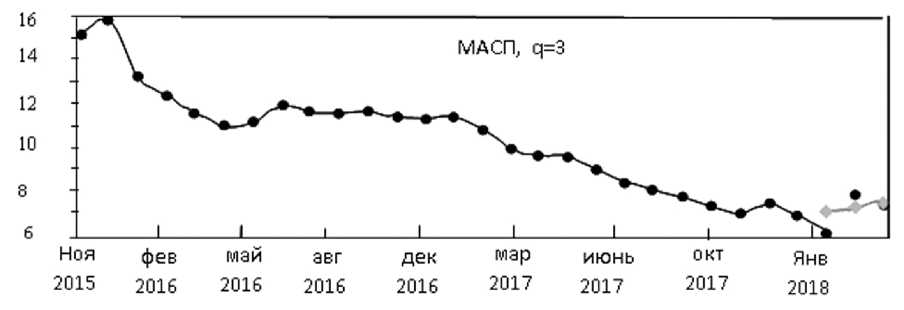
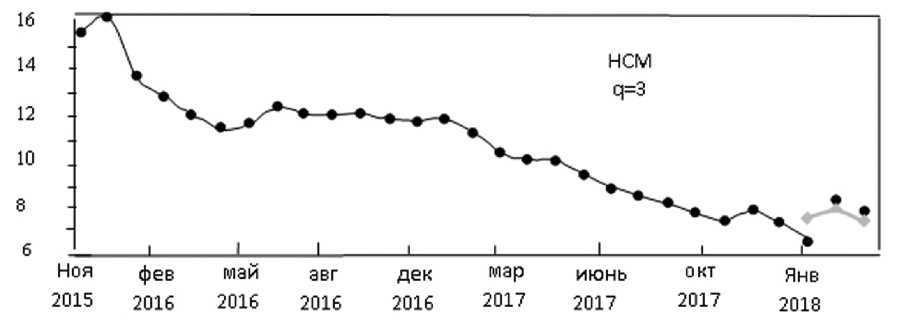
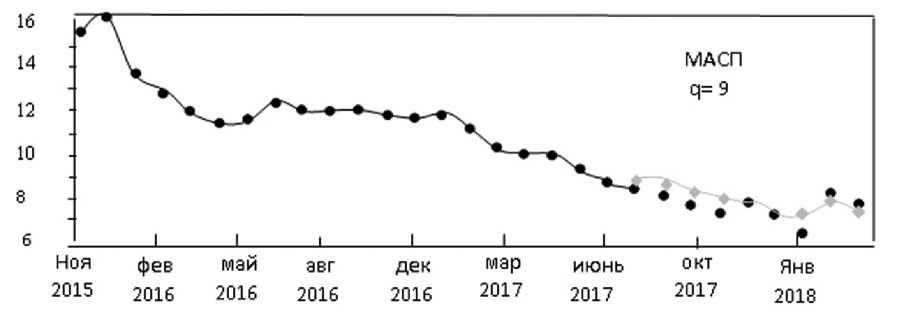
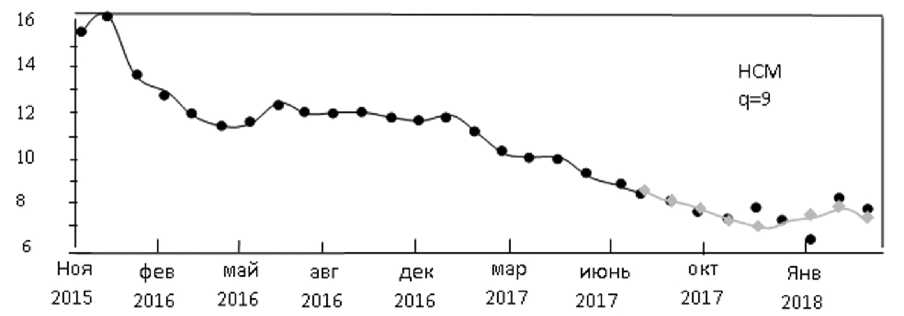
Рис. 2. Средневзвешенная доходность биржевых облигаций в %

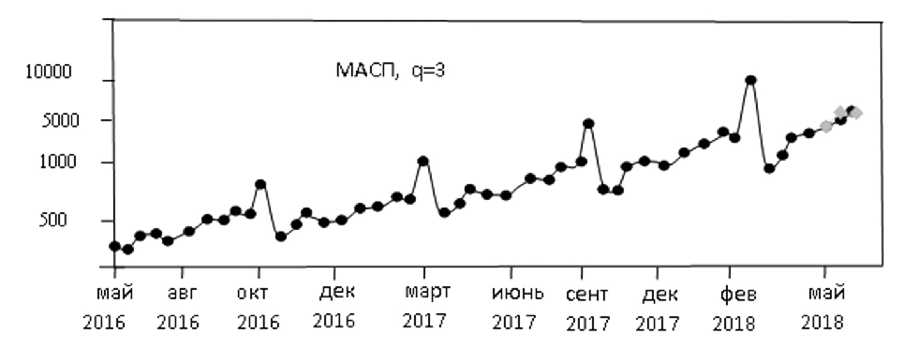
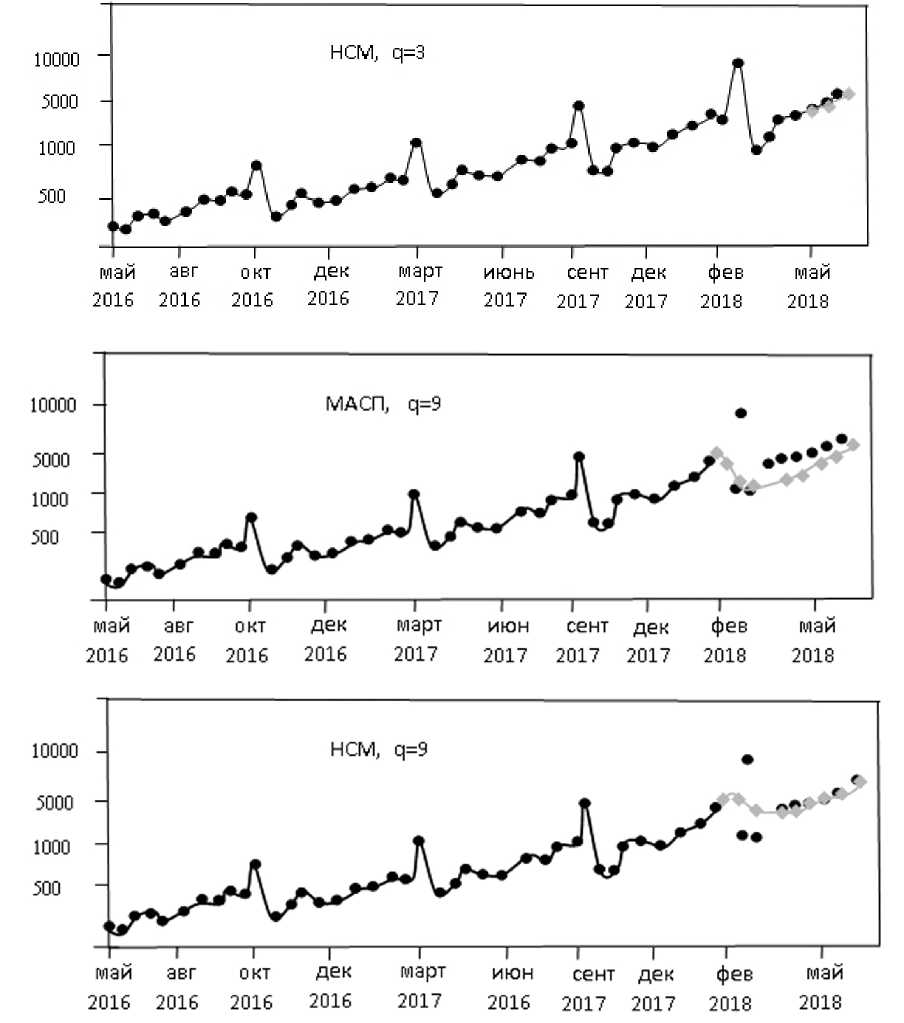
Рис. 3. Суммы поступлений контрактной оплаты па. расчетный счет университета, мли. сум

Таблица 1

Горизонт прогнозирования q = 3

Данные	Характеристики	МАСП	НСМ
Периодичиские	Γ	0,1176	0,0206
нестационарные	Т, с	6,218	1,791
Непериодичиские	Γ	0,0031	0,0038
нестационарные	Т, с	3,114	3,064
Периодичиские	Γ	0,0204	0,0214
нестационарные	Т, с	2,544	2,764

Таблица 2

Горизонт прогнозирования q = 10

Данные Характеристики МАСП НСМ Периодичиские Γ 0,2025 0,1858 нестационарные Т, с 1,763 1,471 Непериодичиские Γ 0,0136 0,0846 нестационарные Т, с 4,778 2,665 Периодичиские Γ 0,0752 0,0506 нестационарные Т, с 8,974 2,624 виде точек и линий выделены серым оттененным цветом, МАСП — метод статистического адаптивного прогнозирования, НСМ — нейросетевой метод прогнозирования.

Для оценки эффективности разработанных методов проведено сравнение основных показателей работы моделей, которые приведены в табл. 1 и 2. В них приняты следующие обозначения: значения коэффициентов точности прогноза в виде среднеквадратического отклонения 7, вычисленного по формуле (21), время работы модели T в секундах.

На основании данных таблиц можно сделать вывод, что в большинстве случаев модель статистического адаптивного прогнозирования справляется с задачей за более длительный временной промежуток, чем нейросетевая модель. Прогноз, построенный с применением НСМ, является более адекватным и качественным, что видно по величине y (табл. 1, 2).

Заключение. Таким образом, видно, что применение нейросетевой модели для построения прогнозирующей модели экономического процесса достаточно обоснованно. В качестве недостатков использования нейросетевых моделей вообще можно отметить значительную зависимость результатов для конкретного экономического процесса от выбранного метода обучения сети.

Сравнение результатов экспериментального анализа при конкретных числовых данных подтверждает применимость нейронных сетей и высокое качество аппроксимации временных рядов и прогнозирования поведения экономической системы. Использование нейросетевых моделей хозяйствующими субъектами может обеспечить получение значительного экономического эффекта, так как позволяет быстро и надежно заблаговременно просчитать возможное развитие событий.