Разработка параллельного алгоритма для информационно-исследовательской системы "MD-Slag-Melt" на основе технологии CUDA

Информационно-исследовательская система (ИИС) MD-SLAG-MELT [1; 3; 7] -программный комплекс, реализующий компьютерные эксперименты по исследованию физико-химических свойств и структуры материалов, ресурс по направлению компьютерного материаловедения.

Базовым методом в ИИС является метод молекулярной динамики (МД), который включает анализ сложного силового взаимодействия между частицами модельной системы. Размер системы (число исследуемых частиц) при МД-моделировании является критически важным. С увеличением числа частиц до 106 линейные размеры модельного куба достигают нанометров, что позволяет получать результаты нового качества, обладающие практической значимостью. Однако расчет систем, содержащих 105-107 частиц, требует серьезных временных затрат и вычислительных ресурсов, что делает невозможным проведение компьютерных экспериментов без привлечения высокопроизводительных вычислений.

В условиях ограниченных аппаратных ресурсов повышение производительности вычислений возможно за счет привлечение графического процессора видеокарты, используемого для компьютерных экспериментов вычислительного устройства (персонального компьютера). Делегирование части вычислений исходной задачи графическому процессору позволит разгрузить центральный процессор, что сократит общее время обработки. Для реализации описанной модели (модель распределенных вычислений MapReduce) необходимо разработать и имплементировать параллельный алгоритм, адаптирующий существующий линейный алгоритм расчета сил межмолекулярного взаимодействия под распределенные вычисления на центральном и графическом процессорах вычислительного устройства.

В статье описан разработанный авторами и реализованный в ИИС MD-MELT параллельный алгоритм расчета сил меж молекулярного взаимодействия. В основе разработанного распределенного алгоритма лежит технология параллельного программирования CUBA (Compute Unified Device Architecture).

Разработка параллельного алгоритма для вычисления результирующих сил взаимодействия между всеми частицами состоит из нескольких этапов: декомпозиция вычислений на независимые подзадачи, выделение информационных зависимостей между подзадачами, масштабирование подзадач - определение необходимой для решения вычислительной схемы и распределение подзадач между исполнительными процессорами [б].

Модель предметной области - коррелированная система N-частиц. Под коррелированной системой понимается система взаимодействующих объектов (частиц), в которой часть характеристик индивидуального объекта или системы в целом зависит от совокупности характеристик всех остальных объектов. Каждая модельная частица имеет набор сохраняющихся и переменных атрибутов. В этом случае МД-моделирование представляет собой численное решение краевой задачи Коши.

Для распределенного МД-модели-рования коррелированной системы N-частиц авторами разработана модель неоднородных дескрипторов. На основе концептуальной модели МД-метода и тщательного анализа программного кода legacy application - локального МД-приложения построены наборы дескрипторов, описывающих бизнес-логику МД-приложения с точки зрения разделения его кода на блоки, пригодные для распределения.

Выделено два класса - одночастичные дескрипторы (Dls(i), Dlv(i)) и агрегаторы (двух- и трехчастичные ф^2(1), П^З^)) дескрипторы). Оба класса предполагают возможность параллельного расчета дескрипторов на разных вычислителях. Однако, если одночастичные дескрипторы можно произвольно распределять по вычислителям, то агрегаторы (содержат эле- менты, описывающие перекрестные отношения разных порядков между одночастичными дескрипторами и/или агрегаторами) являются «зависимыми» от одночастичного дескриптора и рассчитываются на том же вычислительном устройстве, что и «родительский» одночастичный дескриптор. Предложенный подход позволяет отвлечься от конкретного наполнения элементов дескрипторов, перенести акцент с описания физических взаимодействий в системе на информационное описание перераспределения потоков данных между дескрипторами [2; 4].

Метод равномерной загрузки вычислителей

Равномерное распределение задач между исполнительными процессорами повышает общую эффективность вычислений (балансировка системы за счет отсутствия простоев). При этом необходимо учитывать загрузку нитей (единичных процессов, выполняемых на единичных процессорах) -обеспечить не только минимизацию их простоев, но и сокращение количества операций по передаче данных от центрального процессора графическому при вычислени-

Наиболее трудоемкая операция на каждом шаге моделирования - расчет взаимодействий между объектами. Она требует выполнения числа операций, квадратичного по отношению к числу объектов. Для реализации параллельного расчета нужно разделить систему из N объектов на блоки. Каждый блок рассчитывается на отдельном процессоре.

Предварительная схема разбиения задачи на подзадачи: каждый процесс выполняет задачу по подсчету взаимодействия между двумя выбранными частицами системы. Внутри блока (группы программно организованных процессоров) выполняется задача по агрегации результатов выполнения на более низком уровне. Таким образом, результат работы каждого блока -подсчет взаимодействия всех частиц с дан ной. Верхний уровень системы (сетка - совокупность программно организованных блоков) агрегирует результаты, полученные на блочном уровне (взаимодействие каждой частицы со всеми) и передает их хосту.

Первоначально для организации нитей (threads) и блоков (blocks) внутри сетки (grid) использовалась линейная схема [5] организации процессов, что казалось целесообразным, так как на вход алгоритму подается серия одномерных массивов, и каждая нить осуществляет подсчет взаимодействия между двумя определенными частицами.

В алгоритме используется пошаговая проверка эффективности с возможным возвращением на несколько шагов назад. Авторами проведены компьютерные эксперименты, показавшие высокий процент ожидания процессов, что делает представленную декомпозицию частей неэффективной.

Авторами предложен блочный алгоритм, в котором каждый процесс получил задачу по аналитике частицы (взаимодействие выбранной частицы со всеми), а блок процессов - задачу по аналитике группы частиц. Для представленной организации ленточный метод индексирования неприемлем (стал сложным), поэтому для разработки параллельного алгоритма используется блочная схема организации базовых подзадач.

Для оценки корректности этапа разделения вычислений на независимые части используют контрольный список обязательных условий для разбиения: выполненная декомпозиция не увеличивает объем вычислений и необходимый объем памяти; при выбранном способе декомпозиции все процессоры равномерно загружены; выделенных частей процесса вычислений достаточно для эффективной загрузки имеющихся процессоров (с учетом возможности увеличения их количества).

Выделение информационных зависимостей

Учитывая, что передача данных от процессора процессору занимает определенное время и снижает эффективность параллельного алгоритма, ее нужно минимизировать. Оптимальный вариант - перед каждым шагом моделирования передавать всю информацию о системе на каждый процессор. На рисунке 1 показана схема разделения системы из N объектов на блоки с учетом информационных зависимостей.

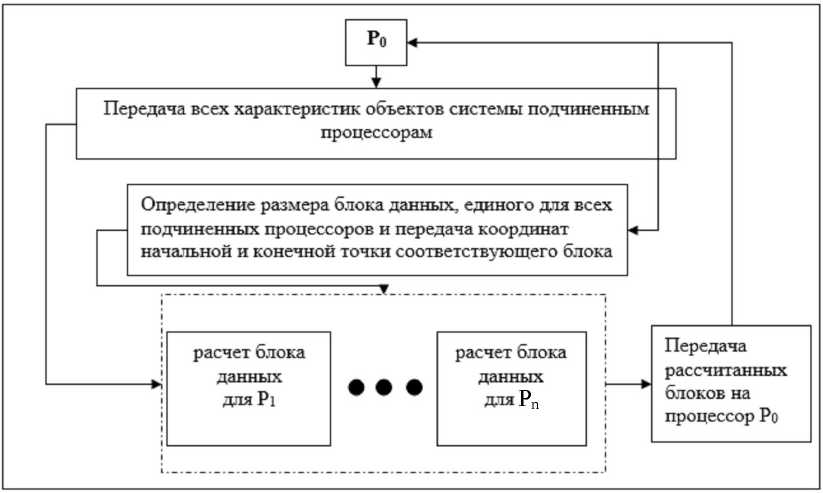
Рис. 1. Разделение системы из N объектов на блоки с учетом информационных зависимостей

Для оценки корректности этапа выделения информационных зависимостей так же, как и для этапа разделения на независимые части, используют контрольный список обязательных условий функционирования: вычислительная сложность подзадач соответствует интенсивности их информационных взаимодействий; интенсивность информационных взаимодействий одинакова для разных подзадач; схема информационного взаимодействия локальна; выявленная информационная зависимость не препятствует параллельному решению подзадач.

Масштабирование и распределение задач по потокам

Параллельный алгоритм называется масштабируемым, если при росте числа процессоров он одновременно обеспечивает увеличение ускорения и сохраняет эф фективность использования процессоров. Масштабирование проводится в случае, если количество имеющихся подзадач отличается от числа планируемых к использованию процессоров. Ниже приведены правила агрегации и декомпозиции подзадач, которые параметрически зависят от числа процессоров, применяемых для вычислений.

На рисунке 2 представлен параллельный алгоритм расчета одного шага моделирования системы из N объектов. Алгоритм является оптимальным для системы с количеством взаимодействий N2.

Рассмотрим более детально систему с количеством взаимодействий (N*(N-l))/2 (каждая частица со всеми без повторений для следующих итераций). На рисунке 3 в матрице отражены системы с количеством взаимодействий М2(слева) и (N*(N-l))/2 (справа), где объекты обозначаются Оъ. ,ОП и серым цветом закрашены области, где не рассчитываются взаимодействия между объектами.

Представленный алгоритм является оптимальными для однородной информационной среды, но его реализация в гетерогенной среде требует доработки. Во-первых, с числом увеличения частиц увеличивается нагрузка на каждый процессор, время выполнения блока расчетов, связанного с i-ой частицей, увеличивается. Во-вторых, из-за гетерогенности среды более мощные компьютеры простаивают, т.к. выполняют свои расчеты быстрее. Для реше ния этих задач создана модель балансировки нагрузки процессоров.

Для оценки правильности масштабирования используют контрольный список обязательных условий функционирования: локальность вычислений не ухудшится после масштабирования имеющегося набора подзадач; подзадачи после масштабирования сохраняют одинаковую вычислительную и коммуникационную сложность; количество задач соответствует числу имеющихся процессоров; правила масштабирования зависят параметрически от количества процессоров.

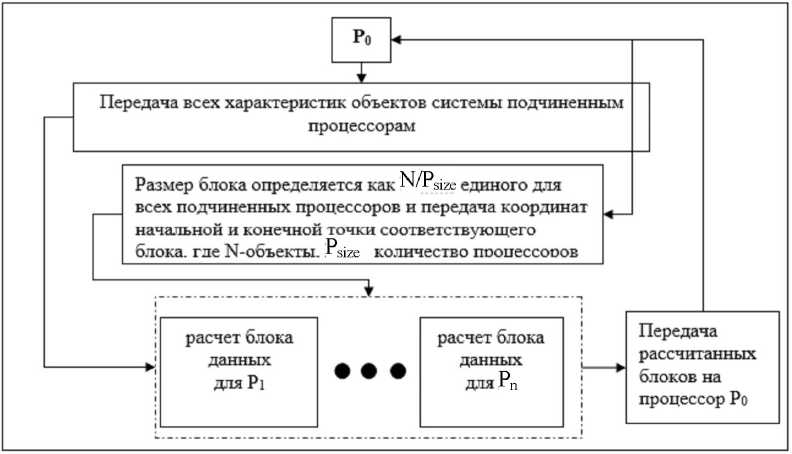
Рис. 2. Алгоритм расчета одного шага моделирования системы из N объектов

	О1	Оз	Оз	■ ■ ■	On
О1				■ • ■
О2				...
Оз				...
...	■ —	...	. - -
On

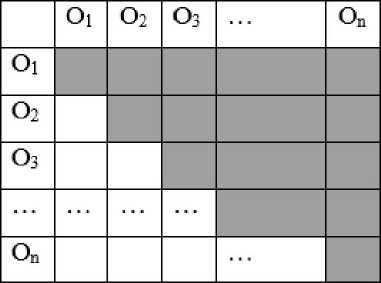
Рис. 3. Количество взаимодействий, выполняемое каждым объектом

Распределение подзадач между процессорами является завершающим этапом разработки параллельного метода. Основ ной показатель успешности выполнения данного этапа - эффективность использования процессоров, определяемая как отно- сительная доля времени, в течение которого процессоры использовались для вычислений, связанных с решением исходной задачи. Пути достижения хороших результатов в этом направлении остаются прежними: обеспечение равномерного распределения вычислительной нагрузки между процессорами и минимизация числа сообщений между ними.

Для оценки правильности распределения использован контрольный список обязательных условий функционирования:

распределение нескольких задач на один процессор не приводит к росту дополнительных вычислительных затрат; существует необходимость динамической балансировки вычислений; процессор-менеджер не является «узким» местом при использовании схемы «менеджер - исполнитель».

Разработанный алгоритм (рис. 4) удовлетворяет всем обязательным пунктам контрольных списков по каждому этапу разработки, также учитываются функциональные и нефункциональные требования.

хост

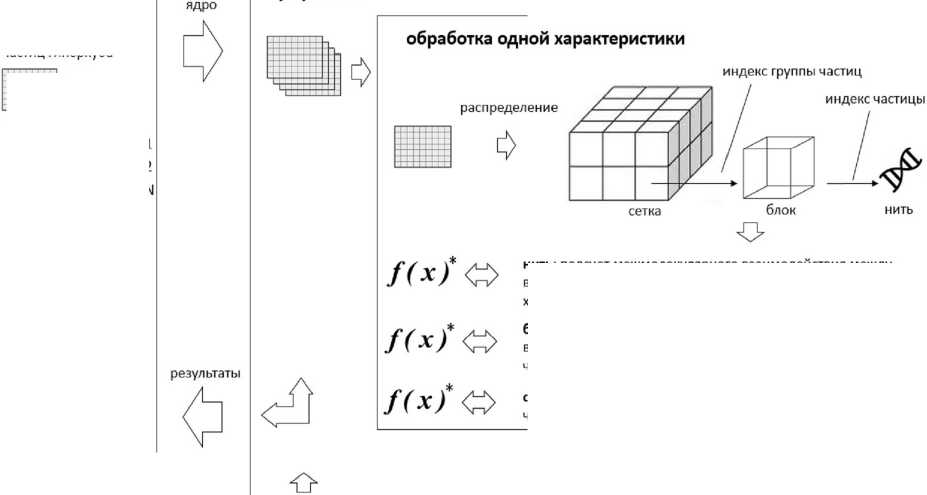
- функция расчета силы между двумя частицами по заданной характеристике повторение итерации для всех характеристик блок: подсчет межмолекулярного взаимодействия между выбранной группой частиц и остальными частицами для каждой частицы выбранной группы по заданной характеристике части объединение с полученными результатами по предыдущим характеристикам

Контрольные суммы для каждой характеристики для обработки сетка: подсчет межмолекулярного взаимодействия между всеми частицами по заданной характеристике части нить: подсчет межмолекулярного взаимодействия между выбранной частицей и остальными частицами по заданной характеристике части

Рис. 4. Алгоритм распределенного вычисления сил межчастичного взаимодействия

Характеристики всех частиц гиперкуба

Роэ\' ПКTQTLI ж'Ллчтж 1А ТЛП И Т IV ТЖ'РПОПЖИМЛ И - Г СзуЛЬ 1Д1 Ы KUMllbitl 1 СрНЫХ JKCIIvpUMCri-

ТОВ

Компьютерные эксперименты проводились на центральном процессоре Intel ® Core i3-4030U CPU 1.90 GHz с ОЗУ, равной 4,00 Gb, и на графическом процессоре с использованием видеокарты NVidia GeForce 820М для приложения, реализующего расчет на CUDA. Результаты компьютер- ных экспериментов, отражающие время вычисления (в секундах) одного программного модуля расчета сил межмолекулярного взаимодействия для параллельного (CUDA) и линейного (host) алгоритмов, представлены в таблице 1.

Таблица 1

Ррэтг ПКТПТ1^Ж L^OmnL. L/TTPITUL ЖУ ^Ж/^Ж'ТТ^И^ЖЛ ия^илт/то ГсзуЛЫ41Ы КОМНЬпЛсрпЫл JKUlCptlMCrl 1 Up

		Количество частиц
		1000	5000	10000	50000	100000	500000	1000000
устройство	CUDA	0,2	2	10	345	1287	42234	589711
	host	15	188	1286	53649	218023	7376529	104063567

Таблица 2

mO9\^ TILTQTLI wy»ZA» «r»w т/АтАеЛ iti ww 3V*Pri0I3I,IM^lUTnD П П<Т Ж^О'ЭЖЮ!^-’/^ L^A ПТ JI IP P T D Q UITTOII rcjyjlbldlbl KUMllbtUlcptlolA лМПСрИМсгПЦр ДЛИ pttjHUl U KUJlHHvLlDd НШсИ

	Количество частиц
	1000	5000	10000	50000	100000	500000	1000000
32	0,5	4,7	22	754	1859	60992	3068950
64	0,2	2,5	10	355	1292	42399	1422241
количество 128	0,3	2,7	11	370	1294	42453	1017201
нитей          256	0,3	2,3	10	360	1297	42563	784484
512	0,3	2,3	11	365	1295	42508	652894
1024	0,2	2,0	10	345	1287	42234	589711

Анализируя полученные результаты, можно сделать предварительное заключение, что реализация параллельного алгоритма дала выигрыш в скорости исполнения модуля подсчета сил межмолекулярного взаимодействия по одной характеристике в более чем 100 раз (усредненное табличное значение ускорения).

В таблице 2 приведены результаты компьютерных экспериментов, отражающих время вычисления одного программного модуля расчета сил межмолекулярного взаимодействия для параллельного

(CUDA) алгоритма при разном количестве потоков (нитей).

Наибольшее ускорение достигается за счет организации блока с максимально возможным количеством нитей. Такая поточная организация позволит увеличить размерность моделируемой системы, но с увеличением числа нитей вырастает потребность в дополнительном выделении памяти на графическом процессоре.

На рисунке 5 представлена кривая ускорения разработанного параллельного алгоритма.

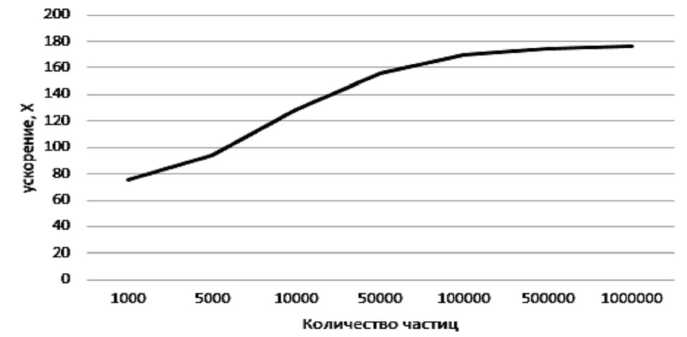
Рис. 5. Кривая ускорения параллельного алгоритма

Пиковое значение скорости наблю- минимальное значение выигрыша в произ-дается возле отметки в 50 тыс. частиц, а водительности составляет 80 раз.