Разработка помехоустойчивого метода разделения секрета на основе применения двухступенчатой системы остаточных классов

Схемы пространственного разделения секрета позволяют делить информацию на n частей и распространять ее среди территориально распределенных n участников, и при восстановлении информации необходимо соединять все части. Схемами разделения секрета, которым для восстановления необходимо k из n частей, называются пороговые схемы разделения секрета.

Изначально такие схемы применялись для хранения секретных ключей и распределенного доступа к стратегическим ресурсам. Такие схемы применяются, если нет доверия одному из участников обмена информации.

В работе проведено исследование метода разделения секрета на группы частей, показано, чем групповое разделение лучше линейного.

При работе схемы пространственного разделения секрета могут подвергается атакам, при которых если злоумышленник является одним из абонентов схемы разделения секрета, то он сможет получить тайную информацию или исказить ее таким образом, что она не сможет быть восстановлена.

Рассмотрим несколько видов таких атак:

• -    один из участников предоставляет ложную информацию, следовательно, секрет будет восстановлен неверно и определить, кто из участников предоставил неверную часть, невозможно;

• -    один из участников фальсифицирует запрос на восстановление секрета, когда остальные участники отправляют данные, он восстанавливает секрет;

• -    один из участников является злоумышленником, он предоставляет свою часть секрета, только узнав все остальные, он может вычислить и отправить свою долю информации, так что секрет восстановится верно и определить, кто «злоумышленник», невозможно.

Отсутствие возможности предупреждения участников разделения секрета о некорректном восстановлении информации может привести к достижению злоумышленником поставленных целей:

• -    легальные участники восстановили неверный секрет;

• -    злоумышленник получил правильный секрет.

Из рассмотренных видов атак следует, что для повышения достоверности восстановления информации следует использовать алгоритмы разделения информации с возможностью контроля ошибок. К таким алгоритмам можно отнести алгоритм разделения информации в обычных вычислениях, основанных на системе остаточных классов (СОК), которая глубоко изучена в теории чисел [7] и активно применяется в цифровой обработке сигналов, обработке изображений, кодах с обнаружением и коррекцией ошибок и криптографических системах [1-3].

Обзор методов преобразования СОК-

ПСС

Для кодов, от которых требуется, чтобы они обладали возможностью обнаружения и коррекции ошибок, необходимо наличие двух групп чисел: информационных и контрольных. В информационную группу входят числа, составляющие значение закодированной величины, а в контрольную дополнительные числа, вводимые для обнаружения и исправления ошибок при передаче.

Система счисления в остаточных классах открывает возможность использования единого помехоустойчивого кода для борьбы с ошибками, возникающими при передаче информации по ка- налам связи и при ее обработке в цифровых системах обработки данных.

Различают избыточную и неизбыточную СОК: последняя должна удовлетворять условию

Лр <^А^Ш где n – число оснований СОК;

Z=1                   Z=1

A – число, представляемое в СОК. Для получения избыточной СОК к числу рабочих оснований n добавляют k избыточных оснований к > 1, тогда п+к

^<Пл. Используя избыточную СОК, можно обнаружить k ошибок.

Пример 1. Рассмотрим пример избыточной и неизбыточной СОК. Пусть дано число л = 66 и система оснований А=²- ^=5, Рз=⁷, Ра =13- Так как неизбыточная СОК должна удовлетворять условию Па<^Па , то основания рабочего диапазона будут А = ²> Рз = 5 , р₃ = 7, а избыточным р₄=13.

Представим это число в СОК А = (0,1,3,1) , для обратного преобразования из системы остаточных классов в позиционную систему счисления СОК → ПСС достаточно иметь три остатка из четырех. Также в данном примере можно обнаружить одну ошибку. Для этого необходимо найти проекции числа А по каждому модулю. Для восстановления числа из СОК в ПСС можно использовать метод, основанный на китайской теореме об остатках, метод Гарнера или метод совместного использования СОК и ОПСС.

Пример 2. Восстановление числа с использованием китайской теоремы об остатках. Восстановление числа из системы остаточных классов в позиционный код при использовании метода, основанного на китайской теореме об остатках [4], необходимо вычислить ортогональные базисы. Для этого рассчитываются величины Р;^:

В_х=т_х-Р_х =1-455 = 455;

В₂ = т₇ • Р₂ = 3• 182= 546;

B₃=m_vP₃ =2-130=260;

В₄ = т₄-Р₄ =8-70 = 560.

Имея значения базисов, вычислим А :

А = \ах ■ Вх + а2 • В2 + а3 • В3+а4- В4\р

Л = |0-455 + 1-546 + 3-260 + 1-560|910 =

= |1886|9„ = 66.

Недостаток метода, основанного на китайской теореме об остатках заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел, а также операция взятия остатка по модулю большого числа.

В методе Гарнера используется полиадическая система счисления, он основывается на идее, что любое число может быть представлено в системе взаимно простых чисел Р\ ■■• Р как [4]:

S = а_л + а₂ • р_{ + а₃ • р_х • р₂+...

+ «„-1 -P\-PV-- Р„-2 +а„-Р1-Р2--‘ Рп-Х ■

Значения а вычисляются таким образом:

а_х = 5,(mod р_хУ, а₂= Qs₂ -а_х) r₁₂(mod р^ ;

^аз = ((^з - Р ) Рз - ^аз )^г2з (^mod Рз);

Р, ЦЦр„-р) z"i„-«2K--«„-ik-i„(mod/?„).

Константы ^" к / можно записать как где 1 < к < j <п .

Подставив значения к / в предыдущие выражения, получим:

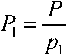
— = 455; Р = 2            ‘

Р

Рз

= 182;

а_х = а_х (mod р_х);

Р 910           Р 910

’= — =--= 130; Р= — =-- = 70.

А ^{7          4} р₄ 13

а₂=Ур_х ¹) mod р₂ • У₂ — а_х )) mod р₂; ^аз ⁼ ((/^kmod р₃ -((^“^mod рЗ х

Ищем веса базисов:

• -из 455- т_х = l(mod2) вычисляем т_х = 1;

  -из 182-m₂ = l(mod5) вычисляем т₂ = 3;

  -из 130-m₃ = l(mod7) вычисляем т₃ = 2;

  -из 10-т₄ = l(modl3) вычисляем т₄ = 8.

Далее вычислим сами базисы:

х (s₃ —а_х) — а₂У mod р₃;

а4 =((z,3"1)mod724 -((^"^mod^x x((/)1”1)mod/)4 -(s4 -d'|)-a2)-a3))mod/?3;

Пример 3. Восстановление числа с использованием метода Гарнера. Для восстановления числа необходимо найти константы ^Tk j •

Г|2	1 2	5	= 3	г13	J_ 2	= 4;т-|4 = 7	J_ 2	= 7; 13
г23 =	1 5	7	= 3	А 4 —	1 5	— 8, г34 = 13		- =2 ^ 13

Найдем значения а_п:

а_х = 5, = 0 ;

а₂ ⁼ (ОГ*) ^m°d Рз ¹ (А ^{- а}\)) ^m°d Рз ⁼

= (3-(l-0))mod5 = 3;

Ц. = ((/^2 ' )^m°d Рз • (С/⁷! ¹) ^m°d Рз X

х(s₃ -aj-а₂ ))mod р₃ =

= (3-(4-(3-0)-3))mod7 = 6;

а₄ = ((Рз"¹ ) ^m°d р₄ • ((Рз"¹ ) mod р₄ х x^p^mod р₄ -(s₄ -a,)-a₂)-a₃))mod р₃ = = (2-(8-(7-(1 —0) —3) —6))modl3 = О.

Тогда

8 = а_х + а₂ -р_х + а₃ ■ р_х • р, + а₃ • р_х ■ р, • р₃ = = 0 + 3-2 + 6-2-5 + 0-2-5-7 = 6б.

Рассмотрим метод совместного использования КТО и ОПСС[5]. Для этого представим ортогональные базисы в ОПСС

Bi = ВП + ВП • Р\ + ВИ •Р\"Р2+-^ВЬ/Р1-Р2--‘РП-^

где В- коэффициенты ОПСС; i,j = 1;2...и.

Тогда коэффициенты ОПС рассчитываются следующим образом

■^ОПСС ^1 (^11’^12’-"’^и ) "*" <^3^31^33,...,Ь₂₍Р +

••• + «„(bny,bn2,...,bn„).

Секрет восстанавливается по формуле

S = а_х + а₂ • р_х + а₃ • р_х- Рз + ...

+ «п-1 -РРР2--- Р„-2 ^и,/Р\-Р2--- РпА ■

Так как В_; mod р_} = О ,\/j > i, то перед первым значащим разрядом будет i – 1 нулей.

Для удобства вычислений базисы можно представить в виде матрицы

Ьц b_X2 ... b_Xn 0 b₂₂ ... b_2n _0 0 ... b_nn

Тогда

^СОК -^	h6nC, 0 0		М27 ^2^22^ 0
		77
при этом ах		7 = 1 ./=1	mod р;

\obbjp_ 1«1б₂„|;_п, ЬМ⁺_Р„_

Пример 4. Восстановление числа с совместным использованием КТО и ОПСС. Представим базисы Bj в ОПСС, тогда b^ :

b\ 1 — 11   bX2 — 2,   bx 3 — 3,   bx 5— 6,

^21 — 0,  b22 — 3,  Ь2з — 5,  b25— 1,

Ьз\ — 0,  ^32 — 0,  b33 — 5,  b35—

Ь^ 1   0,   Ь^з   0,  Ь^з 0,   ^45   ^•

Тогда

"|o<  |o-2|;  |o-3|;|o<"

y        °    I1-3,;   I1-5!?   ^Сз

COK      0       0     |3-5|;   |3.3|;3

_  о       о       0     |i-8|;3_

"0000"

0  3  57

” 0  0  1  11’

0  0  08

a_x = 0, a₂ = 3 , a₃ = 6, a₄ = 0,

S = ax+a2-px+a3 • px-p2+a4 • px-р2-Рз =

= 0 + 3-2 + 6-2-5 + 0-2-5-7 = 66.

Групповой метод разделения секрета

Для увеличения стойкости схемы разделения секрета на основе СОК можно использовать схему с групповым двухступенчатым разделением секрета, рис. 1.

Исходная информация S

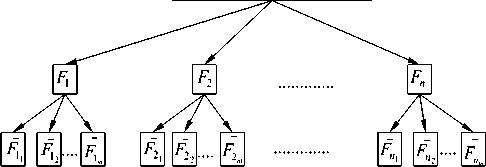
Рис. 1. Структурная схема группового разделения секрета

Работу схемы можно разделить на два этапа.

• 1.    Исходная информация S делится на n частей и распределяется среди лидеров групп FAF....F,,.

• 2.    Информация, принадлежащая лидеру каждой группы F_x;F_...F_n , разделяется на m частей (c^.-^Xc^C.-rJ-kvC-^J-

• Далее эти части могут быть переданы либо по беспроводным сетям передачи данных либо храниться на удаленных серверах.

Исходную информацию предлагается хранить или передавать в виде набора частей, количество которых равно количеству оснований СОК. Введя избыточность среди лидеров групп и среди частей, принадлежащих им, получим пороговую схему, где для восстановления информации достаточно получить от k групп k частей. Уменьшение размера частей, а также их территориальное распределение приведет к снижению нагрузки на линии передачи данных, на серверы для хранения или на ретрансляторы для передачи данных по беспроводным сенсорным сетям. Также с помощью введенной избыточности мы можем локализовать места хранения ошибочных частей и не использовать их для восстановления информации.

Для того чтобы вывести из строя линейную одноуровневую схему, достаточно фальсифицировать k+1 абонентов, а для двухступенчатой необходимо фальсифицировать до (^+ж, где K необходимое число групп для восстановления информации. Мера обнаруживающей способности линейной схемы может быть вычислена со- p -P p -1

гласно [1] как _J1----L ₌ _H--- ,

Используя меру формулу для обнаруживающей способности линейной схемы, модернизируем ее для групповой схемы

(p     p -p     p _p A p _p

• ¹    «1   ^{1        1} 112   ¹ k2 ₊ ¹ nm ¹ km ¹ n ¹ к

P P           P         P ’

\ n\             «2                   nm /        n где m – номер группы.

Таблица 1. Реализация схемы с групповым разделением секрета

Секрет A = 12752322		Группы
		px =229 Fx =228	p2 =233 Fx =232	ft-239 F3 =238	ft =241 F4 =48	ft =251 F5 =16
Л H о Q О S H о cd У	A...5, = 3	0	1	1	0	1
	P1...5, = 5	3	2	3	3	3
	A...53=17	7	11	0	14	13
	=19	0	4	10	10	13
	Pl.5s =23	21	2	8	2	13

В таблице 1 показан пример реализации схемы с групповым разделением секрета. Рассмотрим пример восстановления групповой схемы с применение метода совместного использования КТО и ОПСС для оснований Pv.5_x = ³ ’ Pk.5₂ = ⁵ ’ ^,,=17, ^,₂=19, ^=23, рассчитаем базисы, как показано в первом примере:

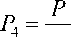
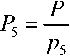
P = 3-5-17-19-23 = 111435;

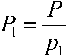
= 37145;

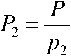
Ш435=22287;

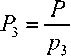
= 6555;

= 5865;

= 4845.

Затем ищем веса базисов:

• - из 37145-m, = l(mod3) вычисляем m_x = 2;

• -    из 22287- m₂ = l(mod5) вычисляем m₂ = 3 ;

• - из 6555- m₃ =l(modl7) вычисляем m₃ =12;

• - из 5865- m₄ =l(modl9) вычисляем «?₄ = 3 ;

• -    из 4845- m₅ = l(mod23) вычисляем ni₅ = 20.

Далее вычислим сами базисы:

B_x =m_vP_x =2-37145=74290;

B₂ =m₂-P₂ =3-22287=66861;

B₃=m₃-P₃ =12-6555=78660,

S₄=m₄-/> =3-5865=17595, B₅=m_vP₅ = 20 -4845 =96900.

Найдем константы T_k j •

	Г25 Г35 =	1 17	| = 14; t31 23 = 19; r45 = 23		1 " 19	= 17; 23
X	^СОЛ' = H |o	■3|	; io-s	i; i	И	; i01 c"
	0     |3	■2|	* |3-3	+ 1'	1-15	*    |3-13l*
=	0	0	|7-8	17 Г i;, i	7-4|	19      1        123 \ p-c
	0	0	0	ii	>■12	l0-3l*
=	0 "0 0 0 0 1 10 0 0 5 0 0 0 0 0 0 ax = 0, a2	0	0 0 0" 7 18 12 21 0 0 0 6_ 1, a3 ='	5, a4	119      I      123 0     |21'20|;3_ = 0, a5 = 0;
	Fx=ax + a2		px + a	•Px"	p2+a3-px +
	^a4-px-	Pl	•p3 + a5-px		■Pi	p3 = 228;
X	У = ^■COK И I1	3i;	I1'5	i:,	|l-6	I1-15!;,'
	0    2	2|	: I2-:	i;,	2-15	r, |2-i3i;,
	0	0	In-:	ii*	11-4	Г In-161*
=	0 0 "13 5 0 4 6 0 0 3 0 0 0 0 0 0 £Z 1      a2	0       0 0       0 6 15" 11 4 11 17 10 14 0 17 = 2,a3 = 1		117 5,a4	4-12 0 = 0,6	119     1           123 ■i;, i4-3i:, |2-20|:,_ z5 = 0;
	Fx -ax+a2		px + a:	•Pv	Рз^з'РЛ
	+ a4'Px'	Pi	•p3 + G	4‘Px	"Pi	^з = 232;

Г12 r15 = J_ 32 ^ 5 ^13 - = 6; r. 4 — ; J ” 5 19 19 = 13; -4; 5 5 = 8; r2 3 _ 1 3 ” 5 5 17 -7; 17 ^2. X3C0K - h; К ’i; 1-5 |i-€ 1-15 123 0 3- zi: 3-3 |3'1C 3-13 Ез = 0 c > 0-8 l°'4i;, 0-1€ •Ез = 0 c 0 ю-С 10-3 Ез 0 c 0 0 8-2( *Ез_ "1 3 5 6 15" 0 1 10 7 18 = 0 0 0 0 0 1 0 0 0 6 13 ° 0 0 0 22 ax = 1, «2 = 4, a3 = 15, a4 = 0, a5 = 0;

Fx = ax+ a2- p x + a3- px- p 2+ a3- p x +

+ a4-px-p2-p3 + a5-px-p2-p3 = 23S;

X 4   =

^COK

lo-C 1°	■з|;	i°-5i;.		i°'6i;,	lO'C
0    3	2Г	3-	3Г	|3-15|*	|з-1з|*
	Is		117	1         119	1         123
0	0	|14	С	|14-4|*	Kiel;,
0	0		0	|ю-12|;,	110-С
0	0		0	0	|2-20|:з
"ООО	0	0"
0 1 10	7	18
0 0 10	5	19	1
ООО	6	13
ООО	0	17
ах = 0,ао	= 1,а	3    3? ^4		= 0,а5 = 0;

F_x=a_x+a₂-p_x + a₃-p_vp₂+a₃-p_x+a₄-p_x-p₂-p₃ + + a₅-pvPi -^3 = 48;

a_x =1, a^ = 0, <7₃ =1, a₄ = 0, a₅ =0

Fx = ax+a2- px + a3- px- p2+a3- px +

+ «4 -Рх-Рз-Рз^аз-Р\-Р2-Рз = ^

	и	13		1-С	и,	ис/		"1	3	5	6	21
	0	1-2		тз!*	11-151*	11-131*		0	2	3	15	13
			5	117	1          119	1         123
Х4 = ^сок	0	0		б<	к 4,	i6.i6i;3	=	0	0	9	14	6
	0	0		0	|16-12|* о	I16-с		0	0	0	2	И
	0	0		0		i6-2o|;3		0	0	0	0	21

Далее таким же образом восстанавливаем и сам секрет из остатков принадлежащих лидерам групп:							Г23 =	1 233	= 438;г24 = 239	1 233	241	= 271;
Г12 —	1 229	233	= 291;г13 =	1 229	= 454; 239		Г25 =	1 233	= 237; г34 = 251	1 239	241	= 361;
С 4 =	1 229	241	= 261; г15 =	1 229	= 308; 251		Г35 =	1 251	= 230; т45 = 251	1 241	251	= 276;
			,228 • 1Г 1           1229	,228 - 175Г    228 • 65Г 1                1233     1               1239			|228.186|;41 |228.202р5|"
			0	1:	7'<,	|57-169|т		'■НС 57-1		5I2i
Хссо		=	0		0	i^-c,	173 •		С 1*73-	12 + 1251		=
			0		0	0		1.182|;4|    |54.219|:S|
			0		0	0		0	148-ЗС,
	"228		57 173	54   47 "
	0		175   69	129 243
=	0		0   235	238 208
	0		0    0	60   6
	_ 0		0    0	0   245 _
	ах	= 228, а2 = 232,0-3			= 238, а 4	= 0,о5 = 0.

Для обнаружения и коррекции ошибок необходимо иметь избыточные основания СОК. Выделим из таблицы 1 информационные и дополнительные основания, таблица 2.

Моделирование группового метода разделения секрета

Данная групповая схема реализована в среде разработки Borland C++ Builder. В качестве объекта разделения было принято 8-битное изображение с разрешением 220×220 точек. Каждый пиксель изображения последовательно переводился в СОК по основаниям рх =229, р2 =233, р3 =239,

Р4 =241, р5 =251, где рх,р2,р3,р4,р5 – это основания лидеров групп. Основания Р\,Рп,Рз являются рабочи- ми, а Ра^Рз – избыточными. Далее основание каждого лидера группы повторно преобразовывалось в СОК по основаниям рпХ = 3, рп2 = 5, Р„з = 17> Р»а =19, р„5 =23, где n – это номер группы и = 1...5. Основания СОК были подобраны таким образом, чтобы три основания были рабочими, а два избыточными. На избыточные основания частей каждой группы накладываем условие абсолютной надежности, что гарантирует достоверность избыточных оснований СОК.

На рис. 2 приведен пример программной реализации группового метода разделения секрета. На нем показано, как исходное изображение делится на пять частей для лидеров групп, и каждый лидер группы затем делится так же на пять частей, после чего изображение восстанавливается.

Система остаточных классов – это система счисления, которая имеет возможность обнару- жения и коррекции ошибок. При восстановлении изображения А из системы остаточных классов если А> Р , то А является ошибочным.

Рассмотрим пример выполнения программы, когда часть информации потеряна. На рис. 3 по-

Таблица 2. Групповая СОК с избыточными основаниями частями и группами

Секрет А = 12752322			Группы
			рх =229 Fx =228	рг =233 ^ =232	/Г =239 F3 =238	^4=241 F4=48	р5=251 F5 =16
			Информационные		Дополнительные
cd Н D Он о о К н о cd	Р\.А = 3	О к о S cd о и К	0	1	1	0	1
	Pl..52 = 5		3	2	3	3	1
	А...3=П		7	11	0	14	16
	Р1..52=19	о л и о н S t! О С О ^	0	4	10	10	16
	Pl.55 = 23		21	2	8	2	16

Рис. 2. Моделирование группового метода разделения секрета казано, что часть информации потеряна, но для локализации достаточно оставшихся изображений.

Поиск локализация ошибок осуществляется путем вычисления проекций числа A по всем осно-

Рис. 3. Восстановление секрета без локализации ошибок ваниям. Так как два основания являются избыточными, то можно найти две ошибки. Рассмотрим численный пример поиска восстановления секрета, если от лидеров групп придет две ошибки.

Пусть дан секрет Л = 300, p_x =13, p₂ = 17, p₃=19, p₄=23, p₅=29. Представим число A в СОК, тогда A = (1,11,15,1,10). Введем ошибку в число, представленное в СОК A = (0,2,15,1,10), тогда при восстановлении A = 1736501, так как A> P, P' =2800733, то можно сказать, что число A ошибочно.

Найдем проекции числа A по двум основаниям:

- по основаниям p_x =13, p₂ =17, P =12673,

A_X2 =300;

- по основаниям p_x = 13 , p₃ = 19 , P¹ = 11339,

Л13 = 6556;

- по основаниям p₂ =17, p₃ =19, P* =8671, ^23 = 6970.

Проекции по всем основаниям, кроме проекции по модулям P_x =13, p₂ =17, больше рабочего диапазона секрета, следовательно, части по основаниям _A =13, p₂ =17 являются неверными, поэтому ошибку можно локализовать и восстановить секрет по основаниям A =19, /?₄ =23, p₅ = 29.

Рис. 4. Локализация ошибок в СОК

На рис. 4 показано, как при потери части информации, достаточной, для потери группы, секрет восстанавливается. Для восстановления секрета необходимо, чтобы в k группах были рабочими K частей, то есть для данного примера достаточно, чтобы в трех группах работало по три клиента. Необходимым условием является также то, чтобы СОК была упорядочена: при неупорядоченной СОК не все пиксели могут быть локализованы.

На рис. 5 показано, как при потере информации, большей, чем это достаточно для восстановления, выглядит восстановленный секрет.

Вывод

В статье представлен метод группового разделения секрета, основанный на системе остаточных классов. Показана его большая обнаруживающая способность в отличие от ли- p -p p -1

нейного метода   л   к _ n   для линейного и pn

(p -P  p -P    p -P 3 pp

• 1 »1   1 И   1 n2   1 kl +   + 1 nm   1 km     1 n

P P        PP для группового), при этом уменьшение размерности частей приводит к снижению нагрузки на линии передачи данных либо на серверы их хранения. Приведены методы локализации оши- бок в СОК, показан способ восстановления информации без коррекции ошибок. Разработано программное обеспечение для моделирования группового разделения секрета на примере разделения цветного изображения с локализацией ошибок. На программной модели показано, что для восстановления секрета групповым методом допустимо потерять больше частей информации, чем при использовании линейного метода. Показана возможность применения разработанной модели для криптографической и некриптографической защиты информации. Работа выполнена при поддержке РФФИ, проект № 13-07-00478-а.