Разработка прогноза покупательского спроса путем экстраполяции тенденции динамического ряда

Введение. Прогнозирование покупательского спроса основано на экстраполяции тенденции динамического ряда товарооборота. Под динамическим рядом товарооборота понимается изменение товарооборота во времени. Если не происходит каких-либо существенных изменений в условиях, формирующих покупательский спрос, то метод экстраполяции позволяет получить достаточно надежные результаты. В противном случае данный метод необходимо дополнить другими методами определения покупательского спроса - расчетно-конструктивным или анкетным.

Статистические методы прогнозирования тенденции динамического ряда подразделяются на две основные группы: методы аналитического выравнивания и экспоненциального сглаживания [2].

Анализ использованной литературы. Многие ученые занимались прогнозированием потребительского спроса на основе экстраполяции тенденций в динамическом диапазоне торговли. К ним относятся В.И. Колемаев, М.И. Баканов, М.В. Мельник, А.Д. Шеремет, Н.И. Щедрин, А.Н. Кархов, И.Е. Гмурман и др.

Методология исследования. В процессе исследования использовались системный подход, абстрактно-логические рассуждения, уравнения гиперболы, динамические ряды и методы аналитического выравнивания.

Анализ и результаты. Сущность метода аналитического выравнивания заключается в нахождении теоретических уровней ряда y _t, которые в минимальной степени отклонялись бы от фактических уровней y . После этого тенденцию ряда можно продолжить, рассчитав уровни ряда на будущий период (год, квартал, декаду), в зависимости от поставленной задачи.

Выравнивание уровней ряда динамики и их экстраполяция производятся по уравнению прямой (тренду), если уровни ряда равномерно растут или уменьшаются. Если изменение тенденции носит характер усиливающегося или затухающего роста, то для экстраполяции применяется соответственно уравнение параболы либо полулогарифмическая кривая. Для экстраполяции криволинейных плавных тенденции можно воспользоваться уравнением гиперболы [3].

Выбор уравнение связи производится на основе графического анализа. Вид уравнений будет несколько отличаться от приведенных ранее тем, что вместо признака – фактора x в уравнение в качестве переменной вводится время t .

Рассмотрим прогнозирование уровней динамического ряда на следующем примере.

Розничный товарооборот по магазину за 2021-2029 гг. (в млн. руб. )

2021 г . - 80,1	2026 г . - 100,8
2022 г . - 82,5	2027 г . - 106,5
2023 г . - 85,8	2028 г . - 114,9
2024 г . - 89,7	2029 г . - 125,7

2025 г . - 94,8

Анализируя изменение уровней ряда, приходим к выводу, что оно носит характер усиливающегося роста. Графический анализ свидетельствует о наличии криволинейной зависимости, напоминающей график параболы. Следовательно, для выравнивания ряда выбираем уравнение параболы yt = a0 + aj + aj2

Составим систему нормальных уравнений:

na о + a i ^ t + a ₂ £ t ² = ^ y ;

a о £ t + a i £ t ² + a 2 £ t³ = £ yt ;

a 0 £ t ² + a i £ t ³ + a 2 £ t⁴ = £ t² y

Построим рабочую расчетную таблицу (табл.1).

Для упрощения расчетов годы условно нумеруются таким образом, чтобы Е t = 0 , тогда и Е t ³ = 0 , а система нормальных уравнений будет иметь вид

Выравнивание динамического ряда по уравнению параболы

Таблица-1

Годы Розничный товарообо-рот.млн. руб. t t2 t3 t4 y • t 2 y • t yt 2021 80,1 -4 16 -64 256 -320,4 1281,6 80,13 2022 82,5 -3 9 -27 81 -247,5 742,5 82,37 2023 85,8 -2 4 -8 16 -171,6 331,2 85,65 2024 89,7 -1 1 -1 1 -89,7 89,7 89,67 2025 94,8 0 0 0 0 0 0 94,73 2026 100,8 +1 1 1 1 100,8 100,8 100,79 2027 106,5 +2 4 8 16 213 426 107,67 2028 114,9 +3 9 27 81 344,7 1034,1 115,55 2029 125,7 +4 16 64 256 502,8 2011,2 124,37 Итого 880,8 0 60 0 708 332,18 6017 880,8 naо + a2 Е t2 = Е у;

a i Е t ² = Е yt ;

a 0 Е t ² + a 2 Е 1 4 = Е t ² у

Поставляя в эту систему соответствующего значения из расчетной таблицы, получаем:

9 a ₀ + 60 a₂ = 880,8

60 a = 332,18

60 a ₀ + 708 a₂ = 6017

Решая уравнение относительно а , получаем

a

332,18

= 5,53.

Далее решаем систему из двух уравнений:

9 a₀ + 60 a. = 880,8   : 9

60 a ₀ + 708 a. = 6017 : 60

Разделив каждое уравнение на коэффициенты при а и вычитая из второго уравнения первое, получим:

a ₀ + 66,6 a. = 97,85

a ₀ + 11,80 a. = 100,28

5,24 a, = 2,43 a₂ = 0,47.

Теперь найдем а :

9 a ₀ + 60 x 0,47 = 880,8 a_o = 94,73

Подставим вычисленные параметры в параметры в уравнение параболы: y_t = 94,73 + 5,53 ? + 0,47 ? ².

Подставляя в данное уравнение значение     t, вычислим теоретические уровни ряда y : *

y = 94,73 + 5,53( - 4) + 0,47( - 4)² = 102,25 - 22,12 = 80,13 и т. д.

Выполнив расчеты, последовательно найдем теоретические уровни ряда, которые выражают общую тенденцию развития.

Для оценки степени приближения теоретических уровней к фактическим необходимо исчислить корреляционное отношение

П =

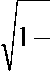
2,263

= 0,99.

Высокое значение корреляционного отношения указывает на то, что кривая подобрана правильно, а теоретические и фактические значения y тесно связаны. В расчете t-критерия Стьюдента в данном случае необходимости нет, поскольку связь очень высокая, и ошибка коэффициента регрессии будет незначительной. Это дает право для прогнозирования объема товарооборота применить уравнение параболы.

Продолжив нумерацию лет, получим следующие значения t :

t 2030 = + 5; t 2031 = + 6.

Тогда прогнозируемый объем товарооборота для этих лет будет равен:

y_t    = 94,73 + 5,53 • 5 + 0,47 • 5² = 134,0 млн. руб.

t 2030

У,    = 94,73 + 5,53 • 6 + 0,47 • 6² = 144,7 млн. руб.

t 2031

Заключение и предложения. Таким образом, следует иметь в виду, что прогноз тем точнее, чем короче период экстраполяции. В работе дано применение экстраполяции тенденции динамического ряда для прогнозирования потребительского спроса на примере данных о товарообороте магазина за некоторый временной отрезок. Выявлена квадратная модель прогнозирования объема товарооборота.