Разработка программного комплекса автоматизированного расчета показателей надежности некоторых элементов интегрированных систем безопасности

В настоящее время проблема количественной оценки надежности интегрированных систем безопасности (ИСБ), функционирующих в условиях воздействия нарушителей и других дестабилизирующих факторов, является достаточно актуальной и на стадии проектирования предусмотрена требованиями государственного стандарта [1], а также рассмотрена в ряде научных публикаций [2,3,6].

В публикациях [4-9] для оценки надежности ИСБ авторы используют методику общего логиковероятностного метода моделирования (ОЛВМ) [10] структурно-сложных технических систем (ССТС), которая характеризуется следующими основными этапами:

• -    принятие и формулировка основных ограничений и допущений;

• -    формирование перечня оцениваемых показателей надежности ИСБ;

• -    определение структурной схемы ИСБ в минимальной конфигурации для формализованной постановки задачи моделирования оценки ее надежности;

• -    формализованная постановка задачи моделирования и расчета, включающая в себя разработку структурно-логической модели (схемы функциональной целостности) ИСБ и задание логического критерия ее функционирования (ЛКФ);

• -    построение логической математической модели (логической функции) работоспособности ИСБ (прямой подход);

• -    построение расчетной вероятностной модели, позволяющей количественно оценить исследуемое свойство надежности ИСБ;

• -    определение исходных данных (вероятностных, временных параметров элементов ИСБ) и расчет оцениваемых показателей надежности с помощью программного комплекса «АРБИТР» [11], анализ полученных данных.

Предметом рассмотрения в настоящей статье является последний из этапов методики общего логико-вероятностного метода моделирования (ОЛВМ) структурно-сложных технических систем – этап определения исходных данных (вероятностных, временных параметров элементов ИСБ). Целью статьи является разработка программного комплекса, предназначенного для автоматизированного расчета показателей надежности некоторых элементов интегрированных систем безопасности.

• 1.    Краткая характеристика проблемы исходных данных при моделировании оценки надежности ИСБ

Определение числовых значений исходных вероятностных (и других) параметров элементов является важной составной частью общей постановки задачи, т.е. первичного структурно-логического моделирования. В практике применения ЛВМ вообще и ОЛВМ в частности разрешимость проблемы исходных данных достигается тогда, когда требуемые параметры P i элементов системы удовлетворяют следующим трем условиям:

• 1.    Являются принципиально определимыми (теоретически или экспериментально) и соответствуют физическому и смысловому содержанию сформулированных исходных бинарных событий.

• 2.    Обладают безусловной статистической устойчивостью на рассматриваемом интервале времени функционирования системы.

• 3.    Обеспечивают правильность комплексирования разных параметров элементов и характеристик элементов средствами вычисления вероятностей сумм, произведений и дополнений множеств случайных событий.

• 2.    Программный комплекс автоматизированного расчета показателей надежности элементов интегрированных систем безопасности - ПК «АРПНЭИСБ»

Решение проблемы исходных данных при моделировании оценки надежности ИСБ требует выполнения специальных работ по их поиску, добыванию, определению и т.п. В большинстве случаев на предельном элементном уровне исходные параметры могут быть определены только экспериментально или при проведении специальных исследований на основе сбора и обработки эксплуатационных данных. Если в качестве элементов используются сложные системные объекты или процессы, то определение соответствующих параметров может осуществляться с использованием любых известных методов анализа на предварительных этапах подготовки к логико-вероятностному моделированию системы в целом.

При задании и определении исходных вероятностных параметров Pi очень важно обеспечить их точное соответствие физическому и смысловому содержанию тех бинарных событий i, которыми представляются собственные характеристики элементов ИСБ. Здесь необходимо, прежде всего, четко различать собственные i и функциональные yi события, сопоставляемые каждому элементу ИСБ. Ве- роятностная характеристика Pi собственного события i является условной в том смысле, что определяет работоспособность данного элемента (элементарного процесса) в заданных, конкретных условиях его работы в системе. В разрабатываемой структурно-логической модели – схеме функциональной целостности (СФЦ) ИСБ такое событие всегда считается простым (бинарным), а вероятность его свершения Pi – известным числовым параметром, например вероятность безотказной работы.

В некоторых случаях собственные параметры Pi элементов могут задаваться не непосредственно, а косвенно, с помощью, например, дополнительных параметров и соответствующих расчетных процедур. Необходимым условием такого задания исходных данных является вычислимость значения собственных вероятностных параметров P i элементов системы.

Четкое определение и уяснение физического смысла собственных и функциональных событий является обязательным условием правильного задания исходных вероятностных параметров элементов и, следовательно, корректности формируемых структурных, логических и вероятностных моделей исследуемых ИСБ.

При моделировании и оценке надежности ИСБ на стадии проектирования в публикациях [5,9] возник вопрос о нахождении количественных показателей надежности кабельных изделий, оконечных элементов (резисторов) в шлейфах сигнализации и вероятности воздействия нарушителя на технические средства ИСБ.

Учитывая громоздкость проведения расчетов показателей надежностей элементов ИСБ по моделям (2,4) вручную, было принято решении о разработке соответствующего программного комплекса (ПК) «АРПНЭИСБ». Для этого использован язык программирования – Delphi (компилятор – Borland Delphi 7.0).

Внешний вид интерфейса ПК «АРПНЭИСБ» представлен на рис. 1.

Приведем результаты систематизации математических моделей, реализованных в программном комплексе «АРПНЭИСБ».

Математическая модель для расчета вероятности воздействия нарушителя на технические средства охраны, установленные на объектах, охраняемых подразделениями вневедомственной охраны, с целью кражи (или другого криминального воздействия) за требуемый период времени :

p  /А _ ^N краж ⁽ t )

нар ( ' N      (A ’ попыток где

P нар

– вероятность воздействия нарушителя на технические средства охраны, установленные на объектах, охраняемых подразделениями вневедомственной охраны, с целью кражи (или другого криминального воздействия) за требуемый период времени t;

N

краж

– общее количество краж, совершенных нарушителями на объектах, охраняемых подраз-

делениями вневедомственной охраны с помощью технических средств, за период времени t ;

N _{попыток} – общее количество попыток проникновений нарушителей, зафиксированных на объектах, охраняемых подразделениями вневедомственной охраны с помощью технических средств, за период времени t ;

t – рассматриваемый период времени, как правило, t =1 год.

Накопленные ГУВО МВД России статистические данные о количестве краж и попыток проникновений нарушителей на охраняемые объекты ежегодно отражаются в соответствующих Обзорах служебной деятельности [13, 14].

Приведем математическую модель для расчета вероятности безотказной работы резистора :

P ( t ) _ exp ( - ^ б • K p • K r ■ K m • K _s • К э ■ K n • t ) ,                                   (2)

где

X = X • К • К • К -К -К - К ^э ^б Kp KR KM KА Ka Kn , где λб – базовая интенсивность отказов резисторов при Т=25 °С, приходящаяся на 1 м длины, [1/ч∙м];

K Р – коэффициент режима работы, зависящий от электрической нагрузки (коэффициента К Н ) и температуры корпуса элемента;

K R – коэффициент, зависящий от номинального сопротивления;

K М – коэффициент, зависящий от номинальной мощности;

K Δ – коэффициент, зависящий от значения допуска на сопротивление;

K э – коэффициент эксплуатации, зависящий от жесткости условий эксплуатации;

К п – коэффициент приемки, учитывающий степень жесткости требований к контролю качества и правила приемки элементов в условиях производства.

Численные значения базовой интенсивности отказов резисторов и коэффициентов K R , K_M , K _А , К э , K_n выбираются из соответствующей справочной литературы [12].

Численное значение K Р рассчитывается по математической модели:

KP = A exp

t окр + ²⁷³

TV

V NT J

exp<

( К Y на

V Ns JV

t ^27 3 ^273 J

H

,

где K нагр – коэффициент электрической нагрузки резистора по мощности;

t окр – температура окружающей среды (корпуса элемента), °С;

• A, B, N T , G, N S , J, H – постоянные коэффициенты, которые принимают значения согласно табл. 1.

  Постоянные коэффициенты модели K Р (3)

  
  

Таблица 1

Виды резисторов постоянных	A	B	N T	G	N S	J	H
Металлодиэлектрические, металлизированные	0,26	0,5078	343	9,278	0,878	1	0,886
Композиционные пленочные	0,06	1,616	328	2,746	0,622	1,198	0,77
Композиционные объемные	0,093	2,194	358	2,019	1,245	1,2	1,362

Математическая модель для расчета вероятности безотказной работы кабельного изделия :

P(t) = exp(-X6 • L,c • K, ■ K, • K, ■ t),                                                    (4)

где

Л = ^ • l_№ • K_t • K • K, э б лс t э п , где λ б – базовая интенсивность отказов кабельных изделий при Т=25 °С, приходящаяся на 1 м длины, [1/ч∙м];

L лс – длина линии связи, [м];

K t – коэффициент, зависящий от рабочей температуры материала, конструкции изоляции и оболочки; K э – коэффициент эксплуатации, зависящий от жесткости условий эксплуатации;

К п – коэффициент приемки, учитывающий степень жесткости требований к контролю качества и правила приемки элементов в условиях производства.

Численные значения базовой интенсивности отказов кабельных изделий и коэффициентов K_э , K_п выбираются из соответствующей справочной литературы [12]. Значение длины линии связи L_лс рассчитывается как можно более точно при проектировании ИСБ, что возможно при тщательном обследовании объекта, выявлении особенностей строительных конструкций, мест установки приборов и прокладки трасс электропроводок.

Численное значение коэффициента K t рассчитывается по математической модели:

Kt = exp

E ■

1

1

—

298

t + окр

1

22 j max P

(t max -25) ■ U 2

L

лс

+ 273

где Е – коэффициент, определяемый материалом изоляции кабельного изделия, см. в [6];

t окр – температура окружающей среды, °С;

t max – максимальная рабочая температура кабельного изделия по ТУ, °С, может быть выбрана из [12];

j max – максимально допустимая по ТУ плотность тока (можно принять 3,5 А/мм²);

U – напряжение в линии связи, В ;

ρ – удельное сопротивление проводника кабельного изделия [Ом∙мм²/м].

Таким образом, созданный ПК «АРПНЭИСБ» позволяет производить автоматизированный расчет:

• -    вероятности воздействия нарушителя на технические средства охраны, установленные на объектах, охраняемых подразделениями вневедомственной охраны полиции, с целью кражи (или другого криминального воздействия) за период времени t;

• -    вероятности безотказной работы резисторов с учетом факторов, влияющих на изменения интенсивности их отказов за период времени t;

• -    вероятности безотказной работы кабельных изделий с учетом факторов, влияющих на изменения интенсивности их отказов за период времени t.

Это позволяет существенно сэкономить временные и трудозатраты при осуществлении оценки надежности ИСБ на стадии проектирования.

Коэффициент, зависящий от рабочей температуры материала конструкции изоляции и оболочки

Коэффициент режима работы зависящий от электрической (коэффициента КН) и температуры корпуса элемента

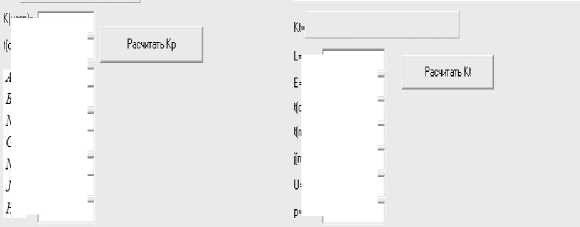
Рис. 1. Внешний вид интерфейса ПК «АРПНЭИСБ»

вероятность безотказной работы резистора Л')=ир(-^,-£,-£„-£,-£,-^^	Вероятность безотказной работы кабельного изделия                                _ ,                   '                               Вероятность воздействия нарушителя на технические средства ^-ех™ s’ я" f .= ’ я J                                охраны установленные на объектах охраняемых подразделениями вневедомственной охраны, с целью кражи (или другого криминального
	Р^___________________________|                            воздействия)
кР= _ &= г	г=                                    ^ V -- ^ямвимГ/
	J                                                           Рнар(1)= _____________________________
^= Г"	К*=                                                        jV J
^= Г              1 ■^- 1                                     1 ^=г	F 1                             1                         N .J №KS№X 5 РасчитатьР(1) Расчигать Рнар(1) |

• 1.    ГОСТ Р 53704-2009. Системы безопасности, комплексные и интегрированные. Общие технические требования.

• 2.    Дурденко В.А., Рогожин А.А., Яковлев А.В. Оценка структурной и параметрической надежности интегрированных систем безопасности охраняемых объектов // Вестник Воронежского государственного университета. Системный анализ и информационные технологии. 2012. №1. С. 61-68.

• 3.    Дурденко В.А., Рогожин А.А. Критериальное моделирование оценки качества функционирования и надежности интегрированных систем безопасности охраняемых объектов // Вестник Воронежского института МВД России. 2012. №1. С. 205-214.

• 4.    Рогожин А.А. Применение технологии автоматизированного структурно-логического моделирования для количественной оценки надежности интегрированных систем безопасности: формализованная постановка задачи // Вестник Воронежского института МВД России. 2013. №2. С. 195-206.

• 5.    Дурденко В.А., Рогожин А.А. Количественная оценка надежности интегрированной системы безопасности на основе логико-вероятностного моделирования // Вестник Воронежского института МВД России. 2013. №2. С. 207-215.

• 6.    Рогожин А.А. Основы построения интегрированных систем безопасности: учеб. пособие. Воронеж: Изд-во Воронеж. ин-та МВД России, 2012. 74 с.

• 7.    Дурденко В.А., Рогожин А.А. Разработка классификации и архитектуры построения интегрированных систем безопасности // Вестник Воронежского государственного университета. Системный анализ и информационные технологии. 2013. №1. С. 61-70.

• 8.    Рогожин А.А., Дурденко В.А., Баторов Б.О. Логико-вероятностное математическое моделирование и оценка надежности системы контроля и управления доступом // Вестник Воронежского государственного университета. Системный анализ и информационные технологии. 2014. №1. С. 5-17.

• 9.    Рогожин А.А., Дурденко В.А., Баторов Б.О. Математическое моделирование и оценка надежности интегрированной системы безопасности при воздействии дестабилизирующих факторов // Вестник Воронежского института МВД России. 2014. №1. С. 79-90.

• 10.    Можаев А.С., Громов В.Н. Теоретические основы общего логико-вероятностного метода автоматизированного моделирования систем. СПб.: ВИТУ, 2000. 145 с.

• 11.    Можаев А.С. Отчет о верификации программного средства «Программный комплекс автоматизированного структурно-логического моделирования и расчета надежности и безопасности систем» (АРБИТР, ПК АСМ СЗМА, базовая версия 1.0). СПб.: СПИК СЗМА, 2007. 1031 с.

• 12.    Боровиков С.М., Цырельчук И.Н., Троян Ф.Д. Расчет показателей надежности радиоэлектронных средств: учеб.-метод. пособие / под. ред. С.М. Боровикова. Минск: БГУИР, 2010. 68 с.

• 13.    Обзор основных результатов служебной деятельности подразделений вневедомственной охраны полиции за 2012 год: письмо ГУВО МВД России от 23 января 2013 г. № 36/183.

• 14.    Обзор основных результатов служебной деятельности подразделений вневедомственной охраны полиции за 2013 год: письмо ГУВО МВД России от 14 февраля 2014 г. № 36/471.