Разработка программного модуля для решения уравнений химической кинетики

Моделирование химических реакций в газах имеет огромную область практических приложений, таких как работа ТЭЦ, бензиновых и дизельных моторов, газофазные химические реакторы.

При численном решении задач химической кинетики возникают трудности, связанные с жесткостью решаемой системы дифференциальных уравнений. Жесткими называют задачи, решение которых содержит компоненты с резко различными характерными временами изменения [1]. При решении жестких систем ОДУ используются многошаговые методы Гира и схемы Розенброка. Однако данные схемы обладают высокой трудоемкостью.

Для численного решения задач химической кинетики в работе [2] предложен метод, основанный на специфической форме правых частей, которыми обладают дифференциальные уравнения, построенные на основе кинетических схем. Это явный алгоритм, имеющий малую трудоемкость и существенно превосходящий известные методы по простоте и надежности.

Численный метод. Предположим, что реагирующая смесь состоит из М компонент. Химический процесс можно описать совокупностью N элементарных стадий:

м

^{У v} in ^A i i=i

м

^ У ^vin^A i , П = О. i=i

Здесь Ai - химические элементы, v'in, v”n - стехиометрические коэффициенты компонента Ai в стадии п.

Система уравнений химической кинетики записывается следующим образом:

N

= У (vin - vin) Wn, i = 1,

at n=1

где Ci - концентрация компонента Ai, wn - скорость элементарной стадии реакции: мм

Wn = kn n(-ci)V'in - k-n n(Ci)V’^, i=ii=i kn, k-n - константы скоростей прямой и обратной стадии реакции, которые определяются из выражений Аррениуса [3]:

k n =A n ^ е ( вт )

.

Здесь A_n - предэкспоненциальный множитель, E_n - энергия активации.

Согласно [2], систему (1) можно представить в следующем виде:

dci

-ТГ = -Ci(p i (c) + 1/Ji(c) с = (С 1 ,с ₂ ,...,С м )  i = 1,.,M.

at

Здесь c_i >  0 , p_i(c) >  0 , ^_i(c) >  0 .

Решение данной системы находится простыми итерациями [2]:

_л5+1   Ct+ T^t(c^s) ⁽ 1+ Tpt(c^s)/2) __s (с + с)

Ct   = ---------------------------2--- ,с = ---й---, С0 = с.

1 + Tp t ⁽c ^{s )} + (тр^С ⁵ )) /2         ²

Здесь C t - решение в исходный момент времени, C t - решение в новый момент времени.

При численном решении системы выполняем две итерации, последующие итерации не повышают порядок точности и ухудшают надежность схемы [2].

Программная реализация. Рассмотрим элементарную стадию реакции следующего вида:

3a + b = c + 2d

Занумеруем компоненты: a — 1 , b — 2, с — 3, d — 4. Для каждой реакции указываются номера компонент a, b,c,d в том порядке, в котором они записаны в реакции. В случае отсутствия некоторой компоненты записываем 0. Также будем полагать, что 0 не могут быть равны одновременно а и b, с и d.

Следующий этап - это запись коэффициентов, стоящих перед каждой компонентой. Коэффициент перед компонентой a - a, b - b, с — с, d — d.

Таким образом, каждая реакция определяется набором параметров a, b,c,d,a,b,c,d, а также предэкспоненциальным множителем А и энергией активации Е. Эти 10 величин определяют структуру элементарной стадии реакции:

S = (a, b, с, d, a., b, c, d, А, Е)                                         (²)

Схема реакции представляется в виде таблицы, число строк в которой равно числу элементарных стадий. Добавление новых стадий сводится к добавлению строк этой таблицы.

Реальные химические задачи описываются большим количеством элементарных стадий с сотнями реагирующих компонент. В данной работе реализован алгоритм, который определяет p t и ^ t автоматически. Этот алгоритм, реализованный в функциях solve_phi и solve_psi, сводится к цепочке последовательных проверок, которые находятся внутри двух циклов: внешнего и внутреннего. Внешний 0...count_substance - позволяет выбрать конкретное вещество. Внутренний 0...count_reaction - позволяет пройти по всем реакциям и найти совпадения, которые впоследствии будут обработаны исходя из условий.

Если ( t - это p для i -того вещества; ^ t - это ^ для i -того вещества; k j - константа скорости для ; -той стадии реакции; с_а - концентрация вещества, с номером a ; с_ь -концентрация вещества, с номером b.

Для phi совпадения ищем среди a и b.

Если исходные вещества реакции одинаковые и оба совпадают с i -тым веществом (а = Ь), то p i = p i + (а + Ъу k j • c_a ^a+b-1 .

Если а равно i -тому веществу и Ь = 0 , то ф , = ф , + а • k j • c_a ^a-1 , если Ь любое другое вещество, то ф , = ф , + а • k j • с_а ^а-1 С ь .

Если Ь равно i -тому веществу и а = 0 , то ф , = ф , + Ь • k j • С ь ^Ь-1 , если а любое другое вещество, то Ф ,= Ф 1 + Ь • k j • c_b ^b-1 c_a .

Для psi ищем совпадения в с и d.

Если с равно i -тому веществу, возникает три случая. Если а = 0, то ^ = ^ + С • k j • c_b ^b ; если Ь = 0, то ty i = ty i + c • k j • c_a^a; если а иЬ разные вещества, то ^ j = ty i + с • k j • c_a^a • r b ^c b .

Если d равно i -тому веществу, возникают также три случая. Если а = 0 , то ty , = ty i + d • k j • Cb^b; если Ь = 0, то ty i = ty i + d • k j • c_a^a; если а и Ь разные вещества, тогда ty i = ty i + d-kj- Ca* • Cb^b.

Вычислительный эксперимент. Описанный алгоритм был реализован на языке программирования С++. Для проверки работы программного модуля была решена система уравнений, описывающая процесс пиролиза этана. В качестве кинетической схемы принята брутто-реакция пиролиза этана, состоящая из двух элементарных стадий [4; 5].

Таблица 1

Схема и кинетические параметры механизма брутто-реакции пиролиза этана

№	Стадия	A„1/c и™л/(моль.с)	Е.Дж/моль
1	С 2 Н 6 ^ С 2 Н 4 + Н 2	1.08Е + 16	2.5Е + 5
2	2С2Н6 ^ С2Н4 + 2СН4	3.16Е + 16	2.7Е + 5

Для записи данных о каждой элементарной стадии реакции пронумеруем компоненты смеси: В 1 = [С₂Н₆], В₂ = [С₂Н₄], В₃ = [Н₂], В₄ = [СН₄].

Соответственно, имеем следующую запись для двух стадий реакции:

(1,0,2,3,1,0,1,1,1.08 • 10¹⁶,2.5 • 10 5 )

(1,0,2,4,2,0,1,2,3.16 • 10¹⁶, 2.7 • 10⁵)

Задачу решаем со следующими начальными условиями:

Т = 800K,c 1 (0) = 1,c₂(0) = 0,c₃(0) = 0,c₄(0) = 0

На рисунке 1 представлены результаты работы программы в момент установления. Полученные результаты хорошо согласуются с результатами, полученными другими авторами [6; 7]. В таблице 2 представлены значения концентраций в установившемся течении.

Сравнение результатов работы программы с полученными ранее

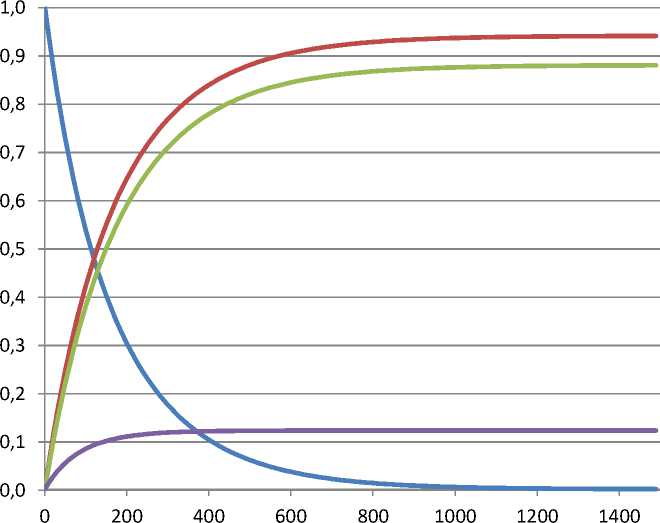
Этан

Этилен

Водород

Метан

Таблица 2

Концентрации	Результаты текущей работы	Результаты, полученные аналитически в [6]
Q	0	0
c2	0.939841	0.94
C 3	0.878950	0.88
	0.121782	0.12

Рис. 1. Изменение концентраций веществ при температуре 800 К, брутто-схема.

Для более точного описания химических превращений в вычислительной практике, как правило, используются схемы с большим количеством элементарных стадий реакции. Покажем, что разработанный программный код дает выигрыш по времени вычислений в сравнении с явным методом Эйлера и методом Розенброка второго порядка, реализованного в системе MATLAB.

Для построения математической модели пиролиза этана принята 15-ти стадийная схема реакции, включающая 12 компонент смеси, представленная в таблице 3 [8].

Таблица 3

Схема и кинетические параметры радикального механизма пиролиза этана

№	Стадия	lgAi,1/c или л/ / (моль • с)	р кДж/ ^ i ’     /моль
1	С 2 Н ^ СН 3 + СН 3	16.0	360.0
2	СН3 ‘ + С 2 Н 6 ^ СН4 + С2Н3	10.0	50.0
3	С 2 Н 5 ^ С 2 Н4 + и -	13.5	170.0
4	И - + С 2 Н 6   > Н . + С2Н3	11.0	40.0
5	н- + С 2 Н 4 ^ С 2 Н'	10.4	8.4
6	СН3‘ + С2Н4 ^ п - С3Н7‘	10.9	33.0
7	п - С3Н7‘ ^ СИ3‘ + С2И4	13.9	137.0
8	С2Н3 + С2Н3 ^ С2Н 4 + С . Н	10.0	8.4
9	п - С 3 Н 7- + С2Н 4 ^ С2Н3 + С 3 Н 6	7.4	27.6
10	СН3' + С2Н4 ^ СН4 + С2Н3‘	8.6	35.0
11	СН3‘ + С2Н3‘ ^ СН4 + С2Н2	9.95	3.2
12	С 2 Н 3 + Н > С 2 Н 2 + Н 2	10.0	0.0
13	С 2 Н 4 ^ ‘ С 2 Н4	15.8	253.0
14	• С 2 Н - + С2Н6 ^ СН3' +п- С3Н7‘	14.7	216.0
15	- С г Н - ^ С 2 Н 4	5.38	0.0

Введем следующие обозначения: В 1 = [С₂Н₆] , В 2 = [С₂Н₄] , В₃ = [Н₂] , В₄ = [СН 4 ], В₅ = [СН з‘ ], В₆ = [С₂И₅ ‘ ] , В₇ = [Н ‘ ] , В₈ = [п - С з Н₇'1 В₉ = [С з Н₆], В₁₀ = [С₂Н з‘ ] , В^ = [С 2 Н1В 12 = [ - С 2 Н ^ ].

Формируем записи элементарных стадий реакции согласно таблице 3 (табл. 4).

Запись стадий реакции для дальнейших расчетов

Таблица 4

№	Запись стадий реакции
1	(1,0’5’0’1’0’2,0,16’360)
2	(5’1’4’6’1’1’1,1,10’10,50)
3	(6’0’2’7’1’0’1’1’13’170)
4	(7’1’3’6’1’1’1’1’11’40)
5	(7’2’6’0’1’1’1,0’10.4,8.4)
6	(5’2’8’0’1’1’1’0’10.9’33)
7	(8’0’5’2’1’0’1’1’13.9’137)
8	(6’6’2’1’1’1’1’1’10’8.4)
9	(8’2’6’9’1’1’1’1’7.4’27.6)
10	(5’2’4’10’1’1’1’1’8.6’35)
11	(5’10’4’11’1’1’1’1’9.35’3.2)
12	(10’7’11’3’1’1’1’1’15’10’0)
13	(2’0’12’0’1’0’1’0’15.8’253)
14	(12’1’5’8’1’1’1’1’14.7’216)
15	(12’0’2’0’1’0’1’0’5.38,0)

Задачу решаем со следующими начальными условиями:

Г = 900 К,с 1 (0) = 1,с₂(0) = 0,.,с₁₂(0) = 0

Были проведены расчеты с использованием трех вышеупомянутых методов, получены хорошо согласованные друг с другом результаты. На рис. 2 представлен результат работы разработанного программного модуля.

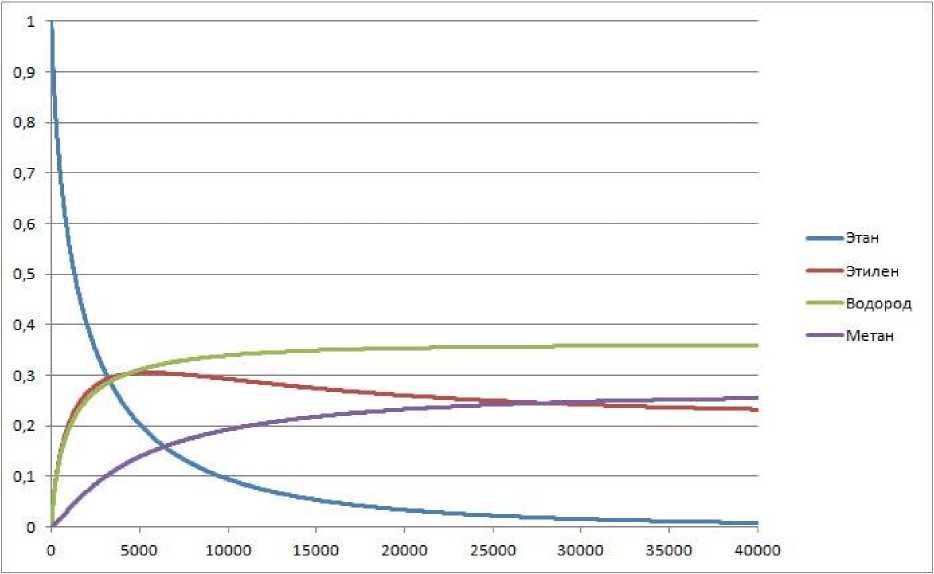
Рис. 2. Изменение концентраций веществ при температуре 800 К.

В таблице 5 представлено время выполнения каждого метода, расчеты велись до времени t = 1 сек .

Время расчета методов

Таблица 5

	Разработанный код на основе метода [2]	Разработанный код на основе явного метода Эйлера	Метод Розенброка второго порядка в системе MATLAB
Время	3 мс	29109 мс	138 мс

Таким образом, разработанный программный код имеет преимущество по времени выполнения по отношению к явному методу Эйлера и широко известному методу Розенброка второго порядка для решения жестких ОДУ, реализованному в системе MATLAB.

Заключение. С помощью разработанного программного модуля можно проводить моделирование задач химической кинетики, включающих любое количество элементарных стадий. В дальнейшем планируется включение данного модуля в разрабатываемый пакет программ [9; 10] для расчета динамики многокомпонентного ламинарного газового потока с учетом химических реакций.