Разработка программного обеспечения для многовариантного прогнозирования экономического события в условиях неопределенности на основе 2-звенной кусочно-линейной экономико-математической модели в четырехмерном векторном пространстве

Прогнозирование – это способ научного предвидения, в котором используется как накопленный в прошлом опыт, так и текущие допущения о будущем с целью его определения. Основная функция прогноза – обоснование возможного состояния объекта в будущем или определение альтернативных путей.

В основе экономического прогнозирования лежит предположение о том, что будущее состояние экономики в значительной мере предопределяется её прошлым и настоящим состояниями. Будущее несёт в себе и элементы неопределённости. Это объясняется следующими моментами: наличие не одного, а множества вариантов возможного развития, неполнота степени познания экономических законов, дефицит и недостаточная надёжность информации. Кроме того, действие экономических законов в будущем зависит не только от прошлого и настоящего состояний экономики, но и от управленческих решений, которые ещё только должны быть приняты и реализованы.

Под методами прогнозирования следует понимать совокупность приёмов и способов мышления, позволяющих на основе ретроспективных данных внешних и внутренних связей объекта прогнозирования, а также их измерений в рамках рассматриваемого явления или процесса вывести суждения определённого и достоверного относительно будущего состояния и развития объекта [1 – 9].

Экономико-математические модели в прогнозировании широко используются при составлении социально-экономических прогнозов на макроэкономическом уровне. К таким моделям относятся: однофакторные и многофакторные модели экономического роста, модели распределения общественного продукта (ВВП, ВНП, НД), структурные модели, межотраслевые модели, модели воспроизводства основных фондов, модели движения инвестиционных потоков и др.

В работах [10 – 14] предложена теория построения n-звенных кусочно-линейных экономико-математических моделей в условиях неопределённости в m-мерном векторном пространстве, дан математический метод определения многовариантного прогнозирования экономического события в условиях неопределённости. К фундаментальным результатам этой теории относятся следующее:

– предложен постулат «пространственновременная определённость экономического процесса в условиях неопределённости в конечномерном векторном пространстве»;

– показана зависимость любого n-го кусочно-линейного векторного уравнения z_n от 1-й кусочно-линейной функции Zj и всех пространственного вида функций влияния неучтённых параметров ш_п(A k ⁿ, a_n_ _1П) , воздействующих на всём предыдущем интервале экономического события следующего вида:

^z

z

= ^z i h + A

n - 1 > 2

^{1 +} ® n ( ^A n , ^a n - 1,n ) ⁺ Z- ' , ^a i - i,i )

i = 2

;

– предложен метод построения прогнозирующей вектор-функции экономического процесса ZN+1(p) с учётом влияния про- гнозирующей функции неучтённых параметров Qn+1(Хn+1,an,n+1) в конечномерном векторном пространстве вида:

■

Z n+1 ( P ) = Z 1 ^ 1 + A

N

^{1 +} Z ^CT i^{( A} i ‘ , ^a i — 1,i ) ^{+ Q} N + 1^{( A} N + 1 , ^a N,N + 1 ) i = 2

Причём, воздействуя функциями влияния неучтённых параметров вида Q N + 1 ( ц N + 1 ; A N + 1 , a N,N + 1 ) с конца последнего векторного уравнения кусочно-линейной прямой ^zNⁿ ( ^ Nⁿ ; A k N , a N,N + 1 ) будут исходить прогнозирующие вектор-функции ^z ^z

^ZN + 1^{( e )} = ^ZN+1 ( H n+1^{; A} N + 1 , ^a N,N + 1 ) , которые представляют собой образующие гиперконической поверхности конечномерного векторного пространства, а точки её направляющей будут формировать линию прогнозирования экономического процесса в конечномерном векторном пространстве.

Далее в работах [15, 16] разработано специальное программное обеспечение для компьютерного моделирования численного построения и определения прогнозных величин экономического события с помощью кусочно-линейных экономико-математических моделей с учётом влияния неучтённых факторов на плоскости.

Данная программа успешно апробирована на многочисленных примерах. Здесь было получено полное соответствие графическим представлениям ранее разработанных плоскостных кусочно-линейных экономико-математических моделей с учётом влияния неучтённых факторов (выпуклостью кверху и книзу), а также (в вопросе установления области изменения прогнозируемой функции выпуклостью кверху и книзу), что свидетельствует о её надёжности. Данная программа апробирована и для кусочно-линейных моделей синусоидального типа [10]. Однако возникающие трудности вычислительного характера требуют создания специального программного обеспечения для компьютерного программирования и создания алгоритма действий для экономических процессов в условиях неопределённости в конечномерном векторном пространстве. В этой связи в работах [17, 18] разработано программное обеспечение для компьютерного моделирования 2звенной кусочно-линейной экономикоматематической модели с учётом влияния факторов неопределённости в 3-мерном и в m-мерном векторных пространствах. Здесь закладываются теоретические основы программирования подобных задач в конечномерном векторном пространстве.

В связи с изложенным в статье, предлагается специальное программное обеспечение для многовариантного прогнозирования экономического события в условиях неопределённости на основе 2-звенной кусочнолинейной экономико-математической модели в четырёхмерном векторном пространстве.

Алгоритм и численная программа для многовариантного прогнозирования экономического события в условиях неопределённости на основе 2-звенной кусочно-линейной модели в 4-мерном векторном пространстве

Для случая 2-звенной кусочнолинейной вектор-функции в условиях неопределённости в 4-мерном пространстве на основе программы Matlab разработаем алгоритм и численную программу для многовариантного прогнозирования экономического события.

Согласно теории [10 – 14], для случая 2звенной кусочно-линейной вектор-функции в условиях неопределённости в четырёхмерном векторном пространстве имеем следующие уравнения и выражения:

z k¹ = а , +ц к 1 (а 2 -5 1 )

kk µ ₁ ² =µ ₁ ¹

k

+µ ₂

(^а з - z k 1 ) ²

( 5 3 - z k 1 )( 5 2 - 5 , )

^z k 2 = а , + ц к² (а 2 -а , )

5 k->   5 к,   . z к-> z22=z11 +(μ12

k -μ ₁ ¹ )

(⁵ з — ^z k 1 )(a 2 -5 1 )

(a 3 - z 1^{k 1} ) ²

(^а з - ^z k 1 )

Cos α _1,2

(z 1^k z 1^{k 2}

-

-

z 1^{k 1} )(z ^k2 ² z 1^{k 1} ⋅ z ^k2 ²

-

-

z ₁ k 1 ) z 1^{k 1}

A( µ 1^{k 2} ) = A = ( µ 1^{k 1} - µ 1^{k 2} )

15 2

-a 1 z 1^{k 1} -a 1

z 1^{k 2} (z 1^{k 1} -a 1 )

к 2 I^{5 к} 2 - ^{5 к} ||5 - ^{5 к} 1 ।     5 к₂ /5 к 5

λ 2 ( µ 1^k2 ) =λ ^k2²

_{µ 2} 2       z₁ -z₁ a₃ -z_{1      z1} 2 (_z1 1 _-a1)

^к 1 -11^к 2      5 ^к 2 Г5^к 2 -5^к 1 )      ^{5    5  5 к} 1    ⁵

µ ₁  - µ ₁ z₁ (z₁ -z₁ ) a₂ -a₁ z₁ -a₁

ω ( λ ^{k 2} , α ) = λ ^{k 2} Cos α

7 (цк-\ _Z —к2Г| + Д Г1_|_  Qk-     уп z2(|1 ) z2 z1 {i+A [1+^2(^2 , а1,2)]} z^li) = zi = 7 +ii(a 2-ai)

/z    7ki \ /z    z \

^.(aL^-J^a^- a) ^{ц ( ц ц} )    ^—z k i ) ²

I^z 2 -^z i|zkⁱ -^z i| 7 i ( 7 kⁱ - 7 i )

-^{z k 1}ll^z₃ -^zM    ⁷ (^{z k} i -^z)

1   3   1       z (z - a₁)

-------------------------------------------------------------- • ----------------------------------:----------------------------

А( Ц 1 ) = ( ц ? ¹ - Ц 1 )

X 2 ( l i ) = тц ²- l i^{1 -} l i

•

I zi

—

a fz - 7ki i     7   7  7ki a z1(z1 Zi )      |a2-ai||zi -ai|

ю₂ (Х₂ ( ц ), а, ₂) = ю₂ ( ц ) = Х₂ ( ц )Cos а, ₂

^Z -⁽ T i^{)= Z} i^{1+A ( ц . Ш-еМ т . )!!

a42(i) = (74)2 = zk2 + a ai (a41(i) - zk2) a2i aii a43 (0 = (Z4)3 = Zk3 + a23   ai3 (a4i(i)- ^i > a2i - aii a44(i) = (74)4 = zk4 + a 4 ai 4 (a4i(i)-zk2) a2i - aii

(a 2 - a i )(a 3 - z k )

^{q i}         < 7 э - z ' )

(7     ^{7 k}i AfZ f1A ^{7 k}2A

_ з-ZL24<12-z^2

^q 2         (^z ₄ (i) - z k ² ) ²

Ц 3 = ( ц - ц ^k 2 )q^ 2

1 ⁷     3-^Zk 2 I I Z HI-^{7 k} 2 I

Iz2(|i) z2 I |a4(i) z2 I q3 =      zi(z2(ii) - Zi-)

z i (z j' - a i )

^q 4     Iz Z I |z k      Z I

Ia- - ai| • Pi' -ai| x3(Ti) = k ц3    • q3 • q4

Ti^{1 -} l i

^{7         7 k}-   fZ        ⁷ k -A

Cosa₂₃ =

2< ц ₁2-z₂_2 • 4 <1)-z^2 Iz -di ) - z k -Ja 4 (i) - z k -j

А ₃ ( Ц 1 ) = ( ц ?¹

^-l i ) •

Ia

- a

—* z ki i

-

ail

z i (z i ^{k i} - a i )

Q₃ (X₃ ( ц ),а_{2 3}) = X₃ ( ц ) • Cosa₂₃

Z 3 ( T i ) = z i {i + А 3 ( Ц 1 )[1 _{+ Ю} - ( Ц 1 ) + 0 3 ( ^ 3 , а -,3 )]}

(i)

Зададим аппроксимационные точки а,, а₂, а₃, а₄ (1) , а также значения параметров p k¹ = p * и p k² = p * . Введем обозначения:

а >  al ; а . >  a 2 ; а ₃----->a3; (а₄),----- > a4(1); p,  >  ml ; p k¹ >  mlkl;

p k² >  m1k2 ; ц₂ > m2 ; p k²---- > m2k2 ; z k¹ >  z1k1; z k ² >  z 1 k 2;

z k² >  z2k2 ; Cos a₁₂ > Cosa12 ; A( p k² ) = A >  A; X₂ ( p k² ) = X ^k ₂ ² >  La2;

® ₂( X k ² , a ₁₂) >  w 2;   z ₂ ( p k² ) >  z2 ; z₁( p ₁) >  z1 ; |z₁(p₁ )| >  z1M ; A( p 1 ) >  Am1 ;

X ₂( p 1 ) >  La2m1;   ro₂ ( X₂ (p,), a,₂) >  w2m1 ; z₂ (p,) >  z2m1 ; |z₂( p )| >  z2m1M ;

(a 4 ) 2 > a4(2) ; (a 4 ) 3 >  a4(3); ( a ₄)₄ > a 4(4) ; q , = q1 ; q 2 = q2 p 3 >  m3;

X₃ ( p,) >  La3m; q₃ = q3; q₄ = q4 ; Cosa₂₃ >  Cosa23 ;

A₃( p 1 ) >  Am1p; Q ₃( X ₃( p 1 ), a ₂₃) >  w3mp ; Z₃ (p₃) >  z3m1p ; |Z₃( p i )| >  z3m1pM ;

Iz (p!)/ Z₃ (p, )| >  (z1M) /(z3m1pM) = Bj ; |z₂ (p, )/Z₃ ^ )| >  (z2m1M) /(z3m1pM) = B₂ ;

I Z 1 ( p 1 )/z ₂ ( p 1 )| >  (z1M)/(z2m1M) = B 3 ; Z 1 (1)/Z 3 (1) >  (z1(1))/(z3m1p(1)) = B 4 ;

z₂ (1)/Z₃ (1) >  (z2m1(1))/(z3m1p(1)) = B₅ ; z₁(1)/z₂(1) >  (z1(1))/(z2m1(1)) = B₆;

Z, (2)/Z₃(2) > (z1(2))/(z3m1p(2)) = B₇ ; z₂(2)/Z₃(2) > (z2m1(2))/(z3m1p(2)) = B₈ ; ^z 1 (2)/ ^z 2 (2) >  (z1(2))/(z2m1(2)) = B₉;   z 1 (3)/Z 3 (3) > (z1(3))/(z3m1p(3)) = B_w ;

z₂ (3)/Z₃ (3) >  (z2m1(3))/(z3m1p(3)) = B_n ;   5 1 (3)72₂(3) >  (z1(3))/(z2m1(3)) = B₁₂

z 1 (4)/Z 3 (4) >  (z1(4))/(z3m1p(4)) = B 13 ; z ₂ (4)/Z 3 (4) >  (z2m1(4))/(z3m1p(4)) = B_M ;

z 1 (4)/ ^z 2 (4) >  (z1(4))/(z2m1(4)) = B 1 ₅.

Пользуясь введёнными обозначениями алгоритм и соответствующая численная программа для системы (1) на языке Matlab будут представлены в виде:

a1=[a11 a12 a13 a14] a2=[a21 a22 a23 a24] a3=[a31 a32 a33 a34] m1k1=(m1)* m2k2=(m2)* a4(1)=a4(1)* for m1=J1:J2:J3 z1k1=a1+m1k1*(a2-a1); m1k2=m1k1+m2k2*((a3-z1k1)*(a3-z1k1)')/((a3-z1k1)*(a2-a1)');

z1k2=a1+m1k2*(a2-a1);

z2k2=z1k1+(m1k2-m1k1)*((a3-z1k1)*(a2-a1)')/((a3-z1k1)*(a3-z1k1)')*(a3-z1k1);

Cosa12=((z1k2-z1k1)*(z2k2-z1k1)')/(sqrt((z1k2-z1k1)*(z1k2-z1k1) ^l )*sqrt((z2k2-z1k1)*(z2k2-z1k1) ¹ ));

A=(m1k1-m1k2)*(sqrt((a2-a1)*(a2-a1)')*sqrt((z1k1-a1)*(z1k1-a1)'))/(z1k2*(z1k1-a1)'); p1=m2k2/(m 1k1-m1k2);

P2=(sqrt((z1k2-z1k1)*(z1k2-z1k1)')*sqrt((a3-z1k1)*(a3-z1k1)'))/(z1k2*(z1k2-z1k1)'); P3=(z1k2*(z1k1-a1)')/(sqrt((a2-a1)*(a2-a1)')*sqrt((z1k1-a1)*(z1k1-a1)'));

La2=p1*p2*p3; w2=La2*cosa12; z2=z1k2*(1+A*(1+w2)) z1=a1+m1*(a2-a1) z1M=sqrt((z1)*(z1)') m2=(m1-m1k1)*(((a3-z1k1)*(a2-a1)')/((a3-z1k1)*(a3-z1k1)')) Am1=(m1k1-m1)*(sqrt((a2-a1)*(a2-a1)')*sqrt((z1k1-a1)*(z1k1-a1)'))/(z1*(z1k1-a1)'); p1m1=m2/(m1k1-m1);

p2m1=(sqrt((z1-z1k1)*(z1-z1k1)')*sqrt((a3-z1k1)*(a3-z1k1)'))/(z1*(z1-z1k1)'); p3m1=(z1*(z1k1-a1)')/(sqrt((a2-a1)*(a2-a1)')*sqrt((z1k1-a1)*(z1k1-a1)')); La2m1=p1m1*p2m1*p3m1;

w2m1=La2m1*cosa12; z2m1=z1*(1+Am1*(1+w2m1)) z2m1M=sqrt((z2m1)*(z2m1)') a4(2)=z2k2(2)+[(a2(2)-a1(2))/(a2(1)-a1( 1))]*(a4( 1)-z2k2( 1)); a4(3)=z2k2(3)+[(a2(3)-a1(3))/(a2(1)-a1(1))]*(a4(1)-z2k2(1)); a4(4)=z2k2(4)+[(a2(4)-a1(4))/(a2(1)-a1( 1))]*(a4( 1)-z2k2( 1)); q1=[(a2-a1)*(a3-z1k1)']/[(a3-z1k1)*(a3-z1k1)']; q2=((a3-z1k1)*(a4-z2k2)')/((a4-z2k2)*(a4-z2k2)'); m3=(m1-m1k2)*q1*q2 q3=(sqrt((z2m 1 -z2k2) *(z2m1-z2k2)') *sqrt((a4 -z2k2) *(a4-z2k2)'))/(z1*(z2m1 -z2k2)'); q4=[z1*(z1k1-a1)']/[sqrt((a2-a1)*(a2-a1)')*sqrt((z1k1-a1)*(z1k1-a1)')]; La3m=[m3/(m1k1-m1)]*q3*q4;

cosa23=((z2m1 -z2k2)*(a4-z2k2)')/[sqrt((z2m1 -z2k2)*(z2m1 -z2k2)')*sqrt((a4-z2k2)*(a4-z2k2)')]; Am1p=(m1k1-m1)*(sqrt((a2-a1)*(a2-a1)')*sqrt((z1k1-a1)*(z1k1-a1)'))/(z1*(z1k1-a1)'); w3mp=La3m*cosa23;

z3m1p=z1*[1+Am1p*(1+w2m1+w3mp)] z3m1pM=sqrt((z3m1p)*(z3m1p)') B1=(z1M)/(z3m 1pM) B2=(z2m 1M/(z3m 1pM)) B3=(z1M)/(z2m1M) B4=(z1(1))/(z3m1p(1)) B5=(z2m1(1))/(z3m1p(1)) B6=(z1(1))/(z2m1(1)) B7=(z1(2))/(z3m1p(2)) B8=(z2m1(2))/(z3m1p(2)) B9=(z1(2))/(z2m1(2)) B10=(z1(3))/(z3m1p(3))

B11=(z2m1(3))/(z3m1p(3))

B12=(z1(3))/(z2m1(3))

B13=(z1(4))/(z3m1p(4))

B14=(z2m1(4))/(z3m1p(4))

B15=(z1(4))/(z2m1(4))

Задаваясь статистическими данными векторов а,, а2, а3, а4(1) и параметрами kk

µ ¹ и µ ² , с помощью предложенной выше численной программы можно проводить глубокие исследования по многовариантному прогнозированию экономического события в условии неопределённости на

end основе 2-звенной кусочно-линейной модели в 4-мерном векторном пространстве.

Пример. В качестве примера рассмотрим случай со следующими заданными статистическими векторами а,, а₂, а₃, а₄ (1) и параметрами µ ₁ ^{k 1} и µ ^k ₂ ² :

a1=[1 1 1 1] a2=[3 2 4.5 5] a3=[6 4 7 6] m1k1=1.5 m2k2=2 a4(1)=10 for m1=1,5:0,5:8

Таблица 1 – Численные значения модулей и соответствующих координат прогнозируемых точек-векторов при различных значениях параметров 5,2879 ≤ µ ≤ 8 и 0 ≤ µ ≤ 0,1777 в 4-векторном мерном пространстве

№	Численные значения векторов z3, Z2, z3 и их модулей	µ 1	µ 2	µ 3
1	2 1 ( ^ 1 ) =[11,5758 6,2879 19,5076 22,1516] Z 2 ( ц 1 ) =[4,2635 2,3159 7,1849 8,1587] Z3 ( р ) =[4,2635 2,3159 7,1849 8,1587] ^( ^ ) =32,3230 | z 2 (^)1=11,9050 Z 3 ( р 1 ) =11,9050	5,2879	2	0
2	z 1 ( p 1 ) =[12 6,5 20,25 23] Z 2 ( ц 1 ) =[4,2872 2,3223 7,2347 8,2172] Z3( р ) =[4,2405 2,2969 7,1558 8,1276] | а1 ( Ц 1 )| =33,5457 z2 ( ^ ) =11,9848 Z 3 ( ц 1 ) =11,8541	5,5	2,1120	0,0139

3	z 1 ( g 1 ) =[13 7 22 25] z2( ц 1 ) =[4,3442 2,3392 7,3518 8,3543] Z3 ( ^ ) =[4,5169 2,4322 7,6441 8,6864] z/ ц ) =36,4280 |z 2 ( Ц 1 )|=12,1732 Z 3 ( Ц 1 ) =12,6572	6	2,3760	0,0466
4	z 1( ц 1) =[14 7,5 23,75 27] z2( ц 1 ) =[4,4025 2,3585 7,4685 8,4905] Z3 ( ц ) =[4,6178 2,4738 7,8337 8,9057] z 1 (^) =39,3105 z 2 ( ^ 1 )1=12,3617 Z 3( Ц 1 ) =12,9662	6,5	2,6400	0,0794
5	Z 1( Ц 1) =[15 8 25,5 29] z2( Ц 1 ) =[4,4617 2,3796 7,5849 8,6260] Z3 ( ц ) =[4,7356 2,5256 8,0505 9,1555] z 1 ( ^ 1) =42,1930 z2( ц 1 ) =12,5502 Z 3 ( Ц 1 ) =13,3206	7	2,9040	0,1122
6	z 1( ц 1) =[16 8,5 27,25 31] z2( Ц 1 ) =[4,5217 2,4022 7,7011 8,7609] Z3 ( ц ) =[4,8575 2,580 8,2729 9,4114] z 1 ( ^ 1) =45,0756 z2( ц 1 ) =12,7388 Z 3 ( Ц 1 ) =13,6846	7,5	3,1680	0,1449
7	Z 1( Ц 1) =[17 9 29 33] z2( Ц 1 ) =[4,5824 2,4260 7,8171 8,8953] Z3 ( ц ) =[4,9813 2,6372 8,4975 9,6696] | Z1 ( Ц 1 )| =47,9583 |z 2 ( ^ 1 )1=12,9274 Z 3 ( Ц 1 ) =14,0526	8	3,4320	0,1777

Таблица 2 - Численные значения отношений модулей и соответствующих координат прогнозируемых точек-векторов при различных значениях параметров 5,2879 <  ^ <  8 и 0 <  ц₃ <  0,1777 в 4-векторном мерном пространстве

ц = 5,2879 Ц 2 = 2 Ц з = 0	|г, ( ц , )|/7 з ( ц , )	Z 2( H 1)/Z 3^1 )	Z1( Ц 1)/Z2( Ц 1)
	2,7150	1
	2 1 (1)/2 з (1)	^_ z 2(1)/Z 3 <1)	Z 1 (1)/Z 2 (1)
	2,7150	1	2,7150
	^_ 2 1 (2)/2 з (2)	^_ Z 2 (2)/Z 3 (2)	Z 1 (2)/Z 2 (2)
	2,7150	1	2,7150
	2 1 (3)/2 з (3)	Z2(3)/Z 3 (3)	Z 1 (3)/Z 2 (3)
	2,7150	1	2,7150
	Z 1 (4)/Z 3 (4)	Z2(4)/Z 3 (4)	Z 1 (4)/Z 2 (4)
	2,7150	1	2,7150
ц = 5,5 ц2 = 2,112 ц = 0,0139	1 z l ( p l )|/|Z 3 ( И 1)|	| Z ! ( Ц | )|/Z з ( Ц | )	|Z 1 ( M 1 )|/|Z , ( M 1 )|
	2,8299	1,0110	2,7990
	Z 1 (1)/Z 3 (1)	Z2(1)/Z 3 (1)	Z 1 (1)/Z 2 (1)
	2,8299	1,0110	2,7990
	Z 1 (2)/Z 3 (2)	Z 2 (2)/Z 3 (2)	Z 1 (2)/Z 2 (2)
	2,8299	1,0110	2,7990
	Z 1 (3)/Z 3 (3)	Z 2 (3)/Z 3 (3)	Z 1 (3)/Z 2 (3)
	2,8299	1,0110	2,7990
	Z 1 (4)/Z 3 (4)	Z 2 (4)/Z 3 (4)	Z 1 (4)/Z 2 (4)
	2,8299	1,0110	2,7990
Ц 1 = 6 ц2 = 2,3760 ц = 0,0466	1 Z 1 ( R 1 )|/Z 3^ )	| Z 2 ( Ц | )|/Z з ( Ц | )	Z1( Ц 1)/Z2 ( Ц 1)
	2,8781	0,9618	2,9925
	Z 1 (1)/Z 3 (1)	Z 2 (1)/Z 3 (1)	Z 1 (1)/Z 2 (1)
	2,8781	0,9618	2,9925
	Z 1 (2)/Z 3 (2)	Z 2 (2)/Z 3 (2)	Z 1 (2)/Z 2 (2)
	2,8781	0,9618	2,9925
	Z 1 (3)/Z 3 (3)	Z 2 (3)/Z 3 (3)	Z 1 (3)/Z 2 (3)
	2,8781	0,9618	2,9925
	^_ Z1(4)/Z 3 (4)	^_ Z 2 (4)/Z 3 (4)	Z 1 (4)/Z 2 (4)
	2,8781	0,9618	2,9925

ц = 6,5 ц2 = 2,64 ц3 = 0,0794	Z 1 ( H 1 )/Z 3 ( ^ 1 )	Z 2 ( O 1)/Z 3( Ц 1 )	Z1( ^ 1) / Z 2( H 1)
	3,0318	0,9534	3,1800
	Z 1 (1)/Z 3 (1)	^_ Z2(1)/Z 3 (1)	Z 1 (1)/Z 2 (1)
	3,0318	0,9534	3,1800
	^_ Z 1 (2)/Z 3 (2)	^_ z2(2)/Z 3 <2)	Z 1 (2)/Z 2 (2)
	3,0318	0,9534	3,1800
	Z 1 (3)/Z 3 (3)	^_ Z 2 (3)/Z 3 (3)	Z 1 (3)/Z 2 (3)
	3,0318	0,9534	3,1800
	^_ Z 1 (4)/Z 3 (4)	^_ Z2(4)/Z 3 (4)	Z 1 (4)/Z 2 (4)
	3,0318	0,9534	3,1800
Ц 1 = 7 ц2 = 2,904 ц = 0,1122	I Z, ( p , )|/Z 2 ( ц , )	| Z2 ( ц l )|/Z j ( ц l )	Z1 ( ^ 1)/Z 2( ^ 1)
	3,1675	0,9422	3,3619
	Z 1 (1)/Z 3 (1)	Z2(1)/Z 3 (1)	Z 1 (1)/Z 2 (1)
	3,1675	0,9422	3,3619
	Z 1 (2)/Z 3 (2)	Z2(2)/Z 3 <2)	Z 1 (2)/Z 2 (2)
	3,1675	0,9422	3,3619
	Z 1 (3)/Z 3 (3)	Z 2 (3)/Z 3 (3)	Z 1 (3)/Z 2 (3)
	3,1675	0,9422	3,3619
	Z 1 (4)/Z 3 (4)	Z 2 (4)/Z 3 (4)	Z 1 (4)/Z 2 (4)
	3,1675	0,9422	3,3619
Ц 1 = 7,5 ц2 = 3,168 ц = 0,1449	I Z, (^)|/Z 2 ( ц , )	| z2 ( ^ , )|/Z 3 ( ^ i )	Z1 ( ^ 1)/Z 2( ^ 1)
	3,2939	0,9309	3,5385
	к Z 1 (1)/Z 3 (1)	^_ Z 2 (1)/Z 3 (1)	Z 1 (1)/Z 2 (1)
	3,2939	0,9309	3,5385
	^_ Z 1 (2)/Z 3 (2)	Z 2 (2)/Z 3 (2)	Z 1 (2)/Z 2 (2)
	3,2939	0,9309	3,5385
	Z 1 (3)/Z 3 (3) 3,2939	Z 2 (3)/Z 3 (3) 0,9309	Z 1 (3)/Z 2 (3) 3,5385
	Z1(4)/Z 3 (4) 3,2939	Z 2 (4)/Z 3 (4) 0,9309	Z 1 (4)/Z 2 (4) 3,5385

Окончание таблицы 2

Ц 1 = 8 ц2 = 3,432 ц3 = 0,1777	ZM)/Zз( Ц 1 )	Z 2 ( H 1)/Z 3^1 )	1 Z , ( ^ 1)|/|Z2( ^ 1)|
	3,4128	0,9199	3,7098
	2 1 (1)/2 з (1)	z 2(1)/Z 3 (1)	Z , (1)/Z 2 (1)
	3,4128	0,9199	3,7098
	^_ z 1 (2)/Z 3 (2)	^_ Z2(2)/Z 3 <2)	Z 1 (2)/Z 2 (2)
	3,4128	0,9199	3,7098
	Z 1 (3)/Z 3 (3)	^_ Z 2 (3)/Z 3 (3)	Z 1 (3)/Z 2 (3)
	3,4128	0,9199	3,7098
	^_ Z 1 (4)/Z 3 (4)	^_ Z2(4)/Z 3 (4)	Z 1 (4)/Z 2 (4)
	3,4128	0,9199	3,7098

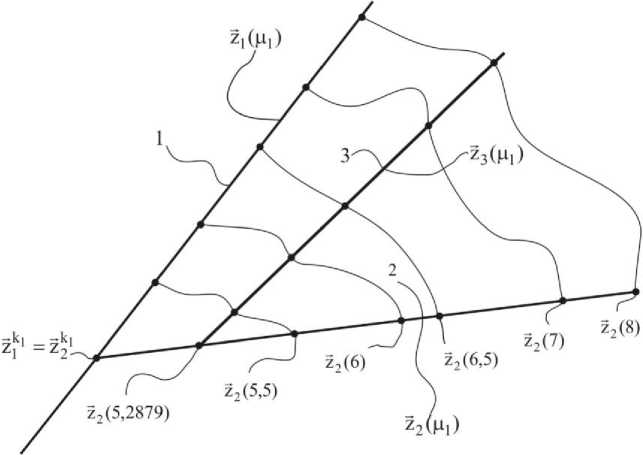
Рисунок – График численных значений модулей и соответствующих координат прогнозируемых точек-векторов при различных значениях параметров 5,2879 < ц <  8 и 0 < ц₃<  0,1777 , вычисленных по разным критериям в 4-мерном пространстве

Данные таблицы 1 и 2 позволяют провести глубокий количественный и качественный анализ по прогнозированию экономического события, то есть численно отработать варианты прогнозных данных экономического со

стояния на последующем этапе, причём как по суммарным показателям в целом, то есть по модулю векторов Z^^, |z₂( ц 1 )| , |Z ₃ (^)| , так и по отдельным экономическим факторам,

n = -11

Сверх этого имеется также возможность сопоставить прогнозные значения экономического события по 3-м критериям: 1) по результатам вычислений по линейному критерию; 2) по результатам вычислений согласно продолжению точек 2-й кусочнолинейной вектор-функции; 3) по результатам вычислений вектор-функции с учётом влияния факторов неопределённости. Схема такого сопоставления прогнозируемых данных графически представлена на рисун-

ке, а в численном виде в таблицах 1 и 2. Здесь для любого значения произвольного параметра ц, изменяющегося в интервале pk²< ц < ц*, имеем соответствующие численные значения z, (ц) z₂ (ц) Z.Cp ), |zM)!, ^z2⁽Ц1)|, Z33⁽Ц1)|.

Для наглядности в качестве примера возьмём значение параметра ц = 6.

Примем во внимание обозначения соответствующих отношений координат векторов ^z₁(ц₁) z₂(ц1) Z₃(ц₁) для (i-1,2,3,4) в виде:

Согласно формулам 2 и таблицам 1 и 2, численно установим соотношения координат векторов Zj (ц) и z₂(ц₁), то есть х_ии x_2i от соответствующих координат прогнозирующей функции ^(ц) с учётом влияния факторов неопределённости в виде:

n11 = n₁₂= n₁₃= 2,8781                (3)

n21 = n22 = n23 = 0,9618 (4) n3, = n32 = n33 = 2,9925 (5) n4 = 2,8781 , n5 = 0,9618 , n6 = 2,9925  (6)

Численное значение (3) показывает, что значения координат прогнозных величин, просчитанные по линейному критерию, в 2,8781 раз выше соответствующих прогнозных координат, просчитанных согласно вектор-функции с учётом влияния факторов неопределённости.

Численное значение (4) показывает, что значения координат прогнозных величин, просчитанные с помощью 2-й кусочнолинейной вектор-функции, составляют 0,9618 часть от значений соответствующих прогнозных координат, просчитанных со- гласно вектор-функции с учётом влияния факторов неопределённости.

Численное значение (5) показывает, что значения координат прогнозных величин, просчитанные по линейному критерию, в 2,9925 раз выше соответствующих прогнозных координат, просчитанных с помощью 2-й кусочно-линейной вектор-функции.

Численные значения (6) указывают на процентное соотношение суммарных показателей вектор-функций, то есть по модулю векторов |21(Ц1)|, z2(Ц1)|, |Z3^)], просчитанных по разным критериям.

С помощью численных данных таблицы 1 несложно установить зависимость координат прогнозирующей вектор-функции в зависимости от параметра µ , то есть Zi⁽ⁱ⁾ ~ Ц1 , Z₂(i) ~ Ц1 и Z3(i) ~ Ц1.