Разработка программы исследования и построения замечательных кривых

Бесконечному множеству уравнений, связывающих две переменные величины и отнесённых к некоторой системе координат, соответствует бесконечное множество кривых самых разнообразных форм. В основу классификации кривых положена природа их уравнений - подразделение уравнений на алгебраические и трансцендентные соответственно тому, будут ли они алгебраическими или трансцендентными в прямоугольной системе координат.

К числу алгебраических кривых относится кривая Штейнера.

Кривую Штейнера можно определить как гипоциклоиду, получаемую в том случае, когда радиус ^r производящего круга в три раза меньше 1

радиуса R неподвижного круга, т.е. когда модуль равен ³ .

Уравнение кривой Штейнера:

~      t         2t x = 2 rcos- + rcos —,

<

t          2t y = 2 rsin--rsin — 33

где ^t - угол поворота производящего круга.

Исключая из (1) параметр ^t , будем иметь:

(x ² + y ² ) ² + 8 rx( 3 y ² - x ² ) + 18 r² (x ² + y ² ) - 27 r⁴

= 0 .

Уравнение (2) показывает, что кривая Штейнера

(2) является

алгебраической линией 4-го порядка.

Свойства кривой Штейнера, присущие ей как гипоциклоиде, таковы:

R_k = 8 r sin —;

• 1)    радиус кривизны в произвольной точке        ²

• 2)    длина дуги от начальной точки до некоторой точки A до

16     2t некоторой точки M (t)

S = — r sin определяется равенством ^{3     4} , соответственно

16 r этому длина одной ветви равняется 3  , а длина всей кривой 16r ;

• 3)    площадь, ограничиваемая кривой, равняется ^{2 п г 2} ;

• 4)    эволюта кривой Штейнера представляет собой также кривую

Штейнера, подобную данной, с коэффициентом подобия, равным 3, и п повёрнутую относительно данной кривой на угол 3

• 5)    натуральное уравнение кривой Штейнера при условии, что длина дуги отсчитывается от точки, для которой t = ^п , записывается в виде R k3 + 9 S ² = 64 r ²

Для анализа кривой Штейнера была написана программа в среде Turbo Pascal. Данная программа с одной стороны демонстрирует основные геометрические свойства представленной кривой, а с другой рассматривает возможные варианты построения данной кривой.

При написании программы для отображения графических изображений применяется графический режим.

Для определения координат точек подключается драйвер мыши. Пользователь нажимает левой кнопкой мыши для определения значений координат точек и при этом указанные координаты записываются в таблицу координат точек. В первой системе координат (слева) показываются варианты при r<0 (r=-0.5, r=-1, r=-1.5), во второй (справа) – когда r>0 (r=0.5, r=1, r=1.5). Причем переход с первой системы на вторую осуществляется при нажатии правой кнопки мыши. Для каждой системы заполняется своя таблица.

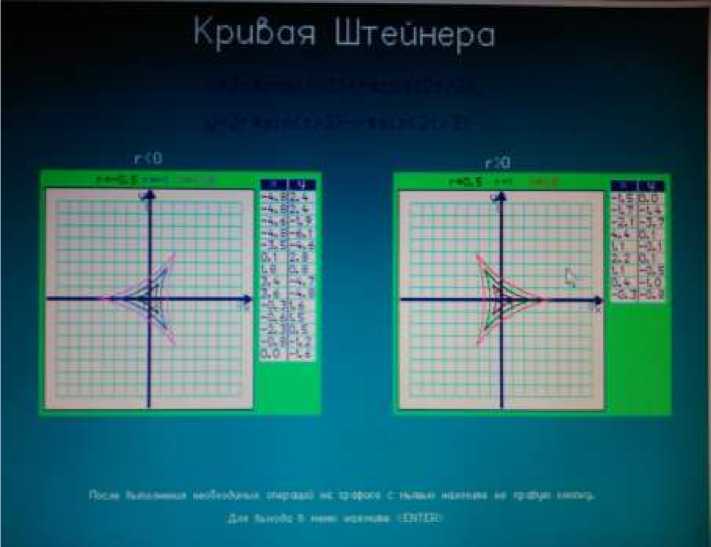
Рис. 1. Построение кривой Штейнера

Написанная программа имеет весьма яркий и дружественный интерфейс, она наглядно демонстрирует основные геометрические свойства кривой Штейнера.

Возможных вариантов кривых, для описания которых составляется программа, достаточно много. Кривая Штейнера является лишь примером построения кривой на плоскости с использованием данной программы. Предлагаемая программа может использоваться в качестве обучающей при проведении занятий по математике при изучении замечательных кривых.