Разработка систем криптографической защиты информации с заданными характеристиками

Выбор типа криптографической защиты для конкретной информационной системы существенно зависит от ее особенностей и должен быть основан на всестороннем анализе требований, предъявляемых к системе защиты информации. Реализация криптографических алгоритмов может быть осуществлена программными, аппаратными или программноаппаратными способами. Основным преимуществом программной реализации является их гибкость, т. е. возможность быстрого изменения криптоалгоритмов, основным недостатком — существенно меньшее быстродействие по сравнению с аппаратными средствами, однако по мере развития вычислительной техники это различие уменьшается. Программно-аппаратные средства объединяют преимущества программных и аппаратных реализаций.

Предлагается модель системы криптографической защиты информации (СКЗИ) с заданными характеристиками, предназначенной для использования в системах и сетях передачи и хранения информации. В СКЗИ реализуются нетрадиционные алгоритмы систем шифрования и электронной цифровой подписи (ЭЦП), разработанные на базе непозиционных полиномиальных систем счисления (НПСС) [1–3], называемых также системами счисления в остаточных классах, системами остаточных классов. В отличие от классических систем остаточных классов в НПСС основаниями являются неприводимые многочлены над полем GF (2). Задаваемые характеристики — длина сообщения и ЭЦП, а также криптостойкость алгоритмов.

Суть разработанных алгоритмов состоит в следующем. При шифровании и подписании электронного сообщения (или блока) длиной N бит cначала формируется НПСС в двоичной системе счисления. Для этого из множества всех неприводимых многочленов степени не выше значения N выбираются рабочие основания

Р 1 ^{( x} ) ,P 2 ^{( x} ) ,...,P S ^{( x} )                                         (1)

над полем GF (2) степени m 1 , m 2 , ...,m s соответственно. В соответствии с китайской теоремой об остатках все основания должны быть различными, в том числе тогда, когда они имеют одну и ту же степень. Основным рабочим диапазоном НПСС является многочлен Ps ( x ) = p ₁ ( x ) Р ₂ ( x ) • • • p _S ( x ) степени

S m =   mi.

i =1

В этой системе любой многочлен F ( x ) степени меньше m имеет единственное представление в виде последовательности остатков (вычетов) от деления его на основания (1):

F ( x ) = ( a i ( x ) , а 2 ( x ) ,..., a s ( x )) .                                     (2)

Здесь F ( x ) = a i ( x )(mod p i ( x )), i = 1 , 2 , ...,S . Позиционное представление этого многочлена при хранении и передаче информации восстанавливается по его непозиционному виду (2):

S

F ( x ) = ^a i ( x ) P i ( x ) , i =1

где Pi (x) = Ps(x)/pi (x). Затем сообщение длиной N бит представляется в виде (2), т. е. интерпретируется как последовательность остатков от деления некоторого многочлена (обозначим его также F (x)) на рабочие основания (1) степени не выше N. Эти основания выбираются из числа всех неприводимых полиномов степени от m1 до mS , удовлетворяющих уравнению к 1 m 1 + к 2 m 2 + ... + kS mS = N.                            (3)

Здесь k i ( i = 1 , S ) — неизвестные коэффициенты (0 < k i < n i ); n i — количество всех неприводимых многочленов степени m i (0 < m i < N ); S = к 1 + к 2 + ... + k s — число выбранных рабочих оснований. Каждое решение (3) задает одну систему рабочих оснований, в которой учитывается порядок их расположения. Полные системы вычетов по модулям многочленов степени m i включают все полиномы степени не выше m i — 1, для записи которых необходимо m _i бит. С увеличением степени неприводимых многочленов их количество быстро растет, вследствие чего значительно увеличивается количество решений уравнения (3) ([см. 4, 5]).

В предложенном алгоритме шифрования процедуре шифрования предшествуют этапы формирования НПСС и генерации псевдослучайной последовательности (ПСП) длиной N бит. Затем шифруемое сообщение длиной N бит представляется в виде (2).

ПСП также представляется в виде последовательности

G ( x ) = ( в 1 ( x ) ,в 2 ( x ) ,...,Ps ( x )) , G ( x ) = P i ( x )(mod p i ( x )) , i = 1 , S.

Тогда криптограмма рассматривается как некоторая функция H ( F ( x ) , G ( x )): H ( x ) = ( ш i ( x ) , ш 2 ( x ) , ...,^s ( x )), H ( x ) = U i ( x )(mod p i ( x )), i = 1 , S .

Полный ключ нетрадиционного алгоритма шифрования составляют все возможные варианты выбора рабочих оснований и псевдослучайной последовательности (ключа) длиной N бит.

Для шифрования используется нетрадиционный метод, в котором элементы последовательности вычетов ш 1 ( x ) , ш 2 ( x ) ,..., W g ( x ) в криптограмме являются наименьшими остатками при делении произведений a i ( x ) в _i ( x ) на соответствующие основания p i ( x ), если в качестве функции H ( F ( x ) ,G ( x )) используется операция умножения [6]:

a i ( x ) e i ( x ) = ш _i ( x )(mod p i ( x )) , i = 1 , ...,S. (4)

Из (4) следует, что при расшифровывании криптограммы H ( x ) по известному ключу G ( x ) для каждого значения e i ( x ) вычисляется обратный (инверсный) многочлен в - 1 ( x ) из условия выполнения следующего сравнения:

e i ( x ) в - 1 ( x ) = 1(mod p i ( x )) , i = 1 , ...,S. (5)

В результате получается многочлен G (x) -1 = (в- 1( x), в - 1( x) ,■■■,вS 1( x)), инверсный многочлену G(x). В соответствии с (4), (5) элементы последовательности вычетов (2) восстанавливаются из условия выполнения сравнения ai = в- 1(x)шi(x)(modpi(x)), i = 1,..., S.

Таким образом, в рассмотренной модели алгоритма шифрования электронного сообщения заданной длины N бит в НПСС полным ключом являются выбранная система оснований p 1 ( x ) , p ₂ ( x ) , ...,p s ( x ), ключ G ( x ) = ( в i ( x ) , в 2 ( x ) ,■■■,в g ( x )) и инверсный ему ключ для расшифровки G ( x ) - ¹ = ( в - 1 ( x ) , в - 1 ( x ) ,...,в д 1 ( x )).

Алгоритм формирования ЭЦП длиной Nk бит для сообщения длиной N бит (Nk ¿ N) включает три шага: построение НПСС; хеширование электронного сообщения до длины Nk путем экстраполяции на избыточные основания; вычисление ЭЦП, которой является криптограмма, полученная при шифровании хеш-значения по описанному выше нетрадиционному алгоритму.

Полный ключ нетрадиционного алгоритма формирования ЭЦП включает все возможные варианты выбора оснований на каждом из трех этапов и псевдослучайной последовательности для шифрования хеш-значения.

В алгоритме формирования цифровой подписи для получения хеш-значения выбираются избыточные основания p g +i ( x ) ,p g +2 ( x ) ,..., p g + и ( x ) из числа всех неприводимых многочленов степени не выше N _k . По модулям этих оснований вычисляются избыточные вычеты a g ₊₁ ( x ) , a g ₊₂ ( x ) , ...,a s ₊ и ( x ) при экстраполяции непозиционного представления многочлена F ( x ). Сумма длин всех избыточных вычетов составляет длину хеш-значения и ЭЦП.

При проверке достоверности ЭЦП адресат расшифровывает ЭЦП, а затем вычисляет хеш-значение принятого сообщения и сравнивает его с хеш-значением, полученным при расшифровке ЭЦП. Если эти два хеш-значения совпадают, то ЭЦП является подлинной.

Криптостойкость описанных алгоритмов определяется всеми возможными отличающимися друг от друга вариантами выбора их полных ключей. Получены формулы криптостойкости нетрадиционных алгоритмов шифрования и формирования ЭЦП. Криптостойкость шифрования сообщения длиной N бит находится по формуле

pkr    1

/( 2 N X k1,k2,...,kS

(( к 1 + к 2 + ... + k g )! С П *С2 2 ... C ks¹)

в которой суммирование распространено на все возможные комбинации коэффициентов k ₁ , k ₂ , ..., k _S , удовлетворяющих равенству (3). Формула криптостойкости формирования ЭЦП имеет вид

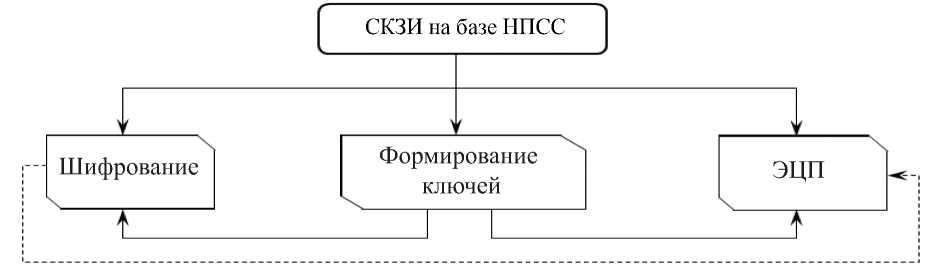
Рис. 1. Схема системы криптографической защиты информации

Psig = 1/2 Nk  X  (((k 1 + k2 + - + ks)! C 1 C2 ••• CS x k1,k2,...,kS

X X  (t1 + t 2 + - + tU )! Cd 11 Cd 2 "■" CdU ) X t1,t2,...,tU

X X   (v 1 + v2 + ■■•+ v")!CvCv2 ■■■ CVW) • v1 ,v2,...,vW где суммирование проводится по всем возможным выборам систем рабочих и избыточных оснований, а также по системам оснований для шифрования хеш-значения. Надежность алгоритмов существенно возрастает с увеличением длин сообщения и ЭЦП, а значит, и с увеличением степени оснований. Исследование алгоритмов показало, что применение полиномиальной системы остаточных классов с двоичными коэффициентами позволяет существенно повысить эффективность алгоритмов за счет распараллеливания вычислительных процедур по каждому из оснований используемых НПСС и специфики арифметики систем счисления в остаточных классах, а также уменьшить длину ЭЦП без потери криптостойкости.

Для представленных выше криптоалгоритмов процесс создания СКЗИ включает три взаимосвязанных блока (или подсистемы), а именно формирование полных секретных ключей, системы шифрования и схемы электронной цифровой подписи (рис. 1).

При моделировании данной СКЗИ основными процессами являются процессы генерации и хранения полных ключей для шифрования и вычисления ЭЦП. Полные ключи будут храниться в базе данных (БД). В подсистеме полных ключей “Формирование ключей” реализуются следующие основные процедуры:

• 1.    Вычисление и хранение неприводимых многочленов заданной степени.

• 2.    Выбор и хранение систем рабочих оснований для сообщения заданной длины.

• 3.    Вычисление псевдослучайной последовательности с использованием алгоритма генерации ПСП [7].

• 4.    Формирование из полученной ПСП ключа G ( x ) для шифрования сообщения и хеш-значения заданной длины и его хранения.

• 5.    Определение и хранение ключа G - 1 ( x ), инверсного G ( x ).

• 6.    Запись в БД полных ключей — конкретной системы рабочих оснований, ключей G ( x ) и G - 1 ( x ).

Раздельное хранение выбранных систем рабочих оснований, ключей G ( x ) и G 1 ( x ) позволяет составлять из них различные комбинации полных ключей.

В блоке “Шифрование” основными модулями являются:

• —    шифрование сообщения длиной N бит;

• —    расшифровка криптограммы.

Блок “ЭЦП” формирует цифровую подпись для электронного сообщения заданной длиной N бит и включает следующие процедуры:

• —    выбор полного ключа из БД, в том числе для заданной криптостойкости;

• —    вычисление ЭЦП;

• —    проверка ЭЦП.

В создаваемой СКЗИ важным является создание БД неприводимых многочленов с двоичными коэффициентами и полных секретных ключей. Полный ключ — это секретный ключ разработанных криптоалгоритмов, состоящий из стандартного секретного ключа (сгенерированной ПСП) длиной N бит и секретной информации самого алгоритма. Обе БД используются в блоках шифрования и электронной цифровой подписи. Из БД неприводимых многочленов выбираются системы рабочих оснований для построения НПСС и вычисления полных ключей различной длины. Найденные составляющие полных ключей записываются в свою БД, для которой определены ее структурные элементы.

Для рассмотренной модели алгоритма генерации секретных ключей предлагается структурная схема модуля формирования БД полных ключей для нетрадиционного алгоритма шифрования. В этом модуле определяются компоненты полного ключа конкретной длины: выбирается система рабочих оснований, генерируется псевдослучайная последовательность (традиционный секретный ключ) и вычисляется инверсный (обратный) для ПСП ключ. В БД может храниться также информация о номере и длине ключа, количестве и степенях выбранных рабочих оснований.

Для СКЗИ с заданной криптостойкостью предполагаются два варианта выбора полного ключа шифрования, поэтому рассматриваются две модели блоков системы шифрования с заданной криптостойкостью, разработанной на базе НПСС.

В первой модели вычисление криптостойкости шифрования проводится в блоке “Формирование ключей”. БД полных ключей дополняется вычисленными по формуле (6) значениями криптостойкости для каждой системы рабочих оснований (рис. 2). В этом случае при шифровании из БД выбирается полный ключ, для которого криптостойкость является не меньше заданной. Таким образом, в этой модели полный ключ выбирается непосредственно из БД полных секретных ключей.

Во второй модели блока системы шифрования с заданной криптостойкостью P _з полный ключ вычисляется в том же блоке. В модуле шифрования проводятся выбор рабочих оснований, вычисление и оценка криптостойкости P расч алгоритма шифрования для выбранной системы оснований, генерация ПСП (ключ G ) и шифрование электронного сообщения заданной длины. Схема модуля шифрования представлена на рис. 3. В этой модели используется только БД неприводимых многочленов с двоичными коэффициентами из блока “Формирование ключей”. В модуле расшифровки полученный шифротекст расшифровывается с использованием инверсного ключа.

Скорость шифрования во второй модели блока шифрования может оказаться меньше, чем в первой, но ее преимущество заключается в уникальности выбранного полного ключа. Эффективность этой модели может быть повышена за счет программно-аппаратной реализации.

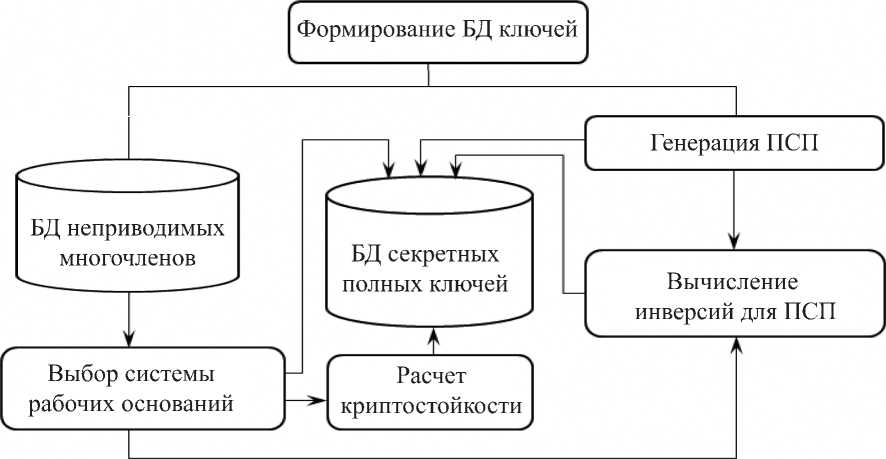
Рис. 2. Структурная схема модуля формирования БД полных ключей, в котором вычисляется и хранится значение криптостойкости шифрования

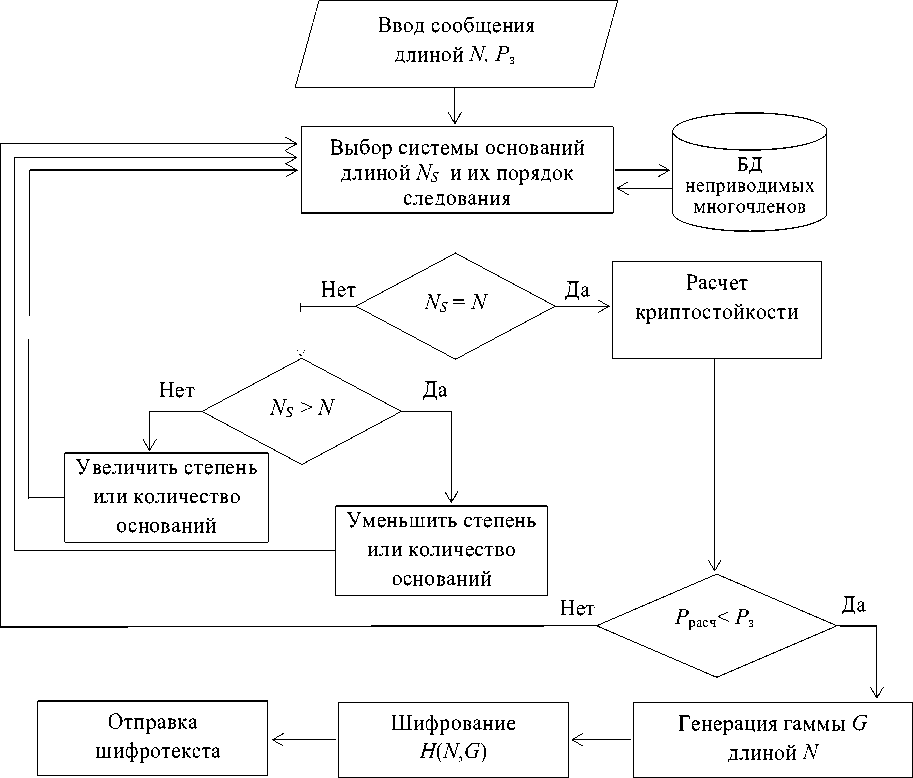
Рис. 3. Формирование полного ключа по заданной криптостойкости в блоке шифрования

Использование различных вариантов определения полных секретных ключей шифрования обусловлено построением гибкой и при необходимости несложно трансформируемой СКЗИ, что позволяет реализовывать различные модели нетрадиционного шифрования.