Разработка системы исследования алгоритмов балансировки имитационным методом

В настоящее время для решения все большего числа научных задач вычислительных ресурсов одной рабочей станции становится недостаточно. Поэтому разрабатываются системы, среды и модели программирования для организации вычислительной системы, развернутой на нескольких рабочих станциях, соединенных высокоскоростной сетью [1].

В организованных таким образом распределенных системах возникают проблемы эффективного использования ресурсов вычислительных узлов сети:

• -    может измениться вычислительная среда, где происходит выполнение приложения, какой-либо вычислительный узел может выйти из строя;

• -    вычислительный узел, на котором выполняется распределенное приложение, занят другими вычислениями, и их доля со временем может возрасти.

В связи с этим необходимо использовать балансировку нагрузки, то есть обеспечение равномерной нагрузки вычислительных узлов. Балансировка реализуется путем переноса части вычислений с наиболее нагруженных вычислительных узлов на менее нагруженные узлы. Цель балансировки загрузки может быть сформулирована следующим образом: исходя из набора задач, включающих вычисления и передачу данных, и сети компьютеров определенной топологии, необходимо найти такое распределение задач по компьютерам, которое обеспечивает примерно равную вычислительную нагрузку компьютеров и минимальные затраты на передачу данных между ними.

Различают статическую и динамическую балансировки. Статическая балансировка выполняется до начала выполнения распределенного приложения. Однако предварительное размещение логических процессов по процессорам (компьютерам) не дает эффекта в случае увеличения нагрузки на вычислительные узлы в процессе исполнения распределенного вычисления. Следовательно, необходима динамическая балансировка, предусматривающая перераспределение вычислительной нагрузки на узлы во время выполнения приложения.

Управление ресурсами и балансировка нагрузки являются ключевыми проблемами эффективного использования ресурсов. Существует множество стратегий и алгоритмов балансировки нагрузки. Встает вопрос о необходимости анализа алгоритмов балансировки для конкретной топологии и интенсивности нагрузки сети для выбора наиболее эффективного алгоритма при определенных условиях.

При исследовании эффективности алгоритмов балансировки встает ряд проблем:

• -    натурные эксперименты имеют высокую стоимость,

• -    подсистема измерения оказывает влияние на ход вычислительного процесса,

• -    системы общего назначения не подходят по ряду критериев.

Поэтому возникает потребность в создании специализированной системы для имитации процесса балансировки загрузки, которая, кроме того, позволит упростить процесс исследования путем автоматизации имитационных экспериментов с алгоритмами динамической балансировки нагрузки.

Задача подобной системы – предоставить инструментальные средства моделирования и анализа процесса балансировки нагрузки для различных сетевых топологий, которые могут быть использованы для анализа стратегий балансировки нагрузки в вычислительной сети.

Метод исследования

В качестве основной модели распределенных вычислений выбрана цепь из асинхронно взаимодейст- вующих процессов, реализованная в программном комплексе GraphPlus. В данной модели процессы, входящие в сеть, взаимодействуют за счет обмена сообщениями. Основа модели – библиотека времени исполнения, являющаяся каркасом для написания распределенных приложений. В данном каркасе ал- горитм управления вычислительным процессом отде- лен от прикладного кода задачи, то есть используется инвертированный поток управления. С точки зрения прикладного программиста программа представляет собой взаимодействие процессов, выполняющих вычисления, описанные прикладным кодом и некоторым управляющим алгоритмом. Детали реализации управляющего алгоритма скрыты от программиста. В более детальном рассмотрении модели распределенных вычислений процессы, выполняющие вычисления, являются резидентами некоторых объектов библиотеки времени исполнения – комнат, являющихся вычислительными узлами. Таким образом, использу- ется модель процессов, причем количество процессов много больше количества узлов. Передача сообщений между резидентами осуществляется через очередь сообщений комнат. Управление комнат осуществляет API операционной системы с помощью системных потоков управления [2].

В связи с тем, что программа определяется моделью GraphPlus, т.е. прикладной код и данные отделены от алгоритма управления вычислительным процессом, используется модель процессов, а также «справедливая в слабом смысле» стратегия планирования, можно внедрить код имитационной подсистемы в готовую систему времени исполнения GraphPlus [3].

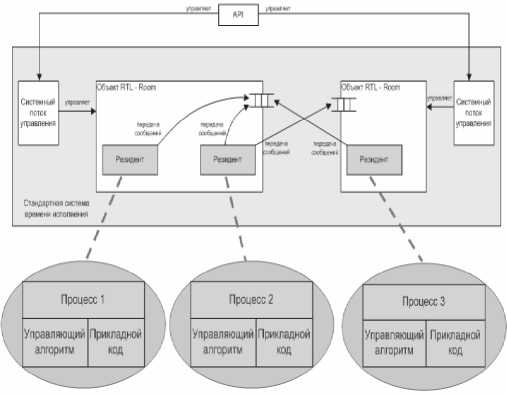
Рис. 1. Концептуальная модель системы. Реальное исполнение

Объекты библиотеки времени исполнения (комнаты, резиденты) могут быть задействованы в имитационном моделировании без внесения изменений в их реализацию. Стандартная система времени исполнения может быть заменена системой имитационного моделирования, состоящей из монитора моделирования, управляющего объектами RTL через модели системных потоков управления; подсистемы балансировки; подсистемы отображения результатов, хранения и настройки параметров экспериментов, важной частью которой является подсистема сбора статистики. Принцип произведения замены стандартной системы времени исполнения на систему имитационного моделирования изображен на рис. 1 и рис. 2.

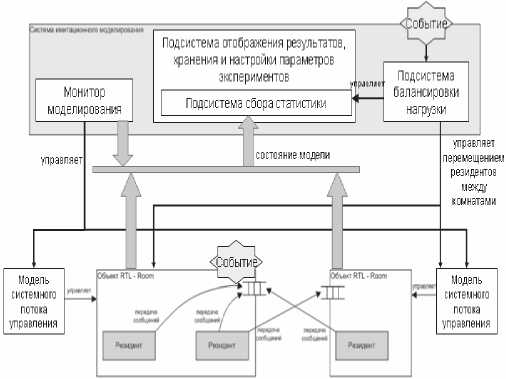
Рис. 2. Концептуальная модель системы. Имитаци- онное исполнение

В ходе имитационного эксперимента при добавлении сообщения в очередь комнаты возникает событие разбалансировки, активизирующее подсистему балансировки, которая анализирует нагрузку на узлы – комнаты и в случае необходимости производит перемещение резидентов – задач между узлами. Нагрузка на узел характеризуется длиной очереди сообщений. При возникновении события происходит сбор статистики о нагрузке на узлы, которая в дальнейшем используется для построения графиков, вычисления эффективности алгоритма, вычисления характеристик узлов: средней нагрузки (длины очереди сообщений), среднего квадратичного отклонения нагрузки каждого узла.

Для сравнения различных алгоритмов балансировки был введен критерий эффективности. Эффективность алгоритма балансировки – это процент времени, в течение которого система выполняла полезные вычисления. Эффективной нагрузкой вычислительной сети будем считать процент задействованных в данный момент в вычислениях узлов. Так как нагрузка вычислительного узла измеряется длиной очереди сообщений, узел является задействованным в вычислениях (не простаивающим), если очередь его сообщений не пуста. Эффективная нагрузка вычислительной сети является нормализованной по количеству узлов результата сложения эффективностей нагрузки каждого узла.

Таким образом, эффективность алгоритма ба- лансировки вычисляется по следующим формулам:

/обЩ(?)= —     – эффективная загрузка вычисли тельной сети, где – мгновенное значение эффективности нагрузки i-го узла; n – число узлов сети;

1 т е = — \J ,- (/)й – эффективность алгоритма баланси-Г 0 0 Щ ровки нагрузки вычислительной сети; T – продолжи- тельность выполнения вычислений в модельном вре- мени.

Экспериментальное обоснование

Целью проводимых экспериментов была проверка работоспособности системы на примере двух алгоритмов балансировки при имитации метода с одномерной декомпозицией данных. Для достижения данной цели было проведено три вида экспериментов.

Проведение серии имитационных экспериментов. Рассмотрим работу системы на примере исследования эффективности статического и динамического алгоритмов балансировки – это доля задействованных в вычислениях узлов сети на время эксперимента. Соответственно, в случае одного узла эффективность алгоритма должна быть равна 1. В случае двух узлов при использовании любого алгоритма не менее 0,5. Для проверки этих предположений была проведена серия имитационных экспериментов для случая разбиения задачи на три резидента и исполнения на сети, состоящей из одного, двух, трех узлов. Распределять задачу, разбитую на три резидента, на четыре узла нецелесообразно, так как один узел будет простаивать, а эффективность алгоритма не может быть больше 0,75.

Для сравнения времени выполнения вычислений был проведен имитационный эксперимент для одного вычислительного узла без алгоритма балансировки.

Таблица 1. Результаты исследования алгоритма балансировки, n – число узлов

п	Тип балансировки	Время вычислений, С	Эффективность
1	-	480,3	1
2	Без балансировки	480,3	0,5
2	Статическая	330,5	0,898966
2	Динамическая	330,5	0,899234
3	Статическая	300,2	0,599489
3	Динамическая	300,2	0,599311

Результаты исследования, приведенные в таблице 1, подтверждают сделанные предположения, а также показывают, что эффективность динамической балансировки не хуже статической, а иногда даже лучше.

Оценка эффективности алгоритма динамической балансировки. Оценка эффективности алгоритма динамической балансировки была проведена с помощью серии имитационных экспериментов для случая разбиения задачи на 10 резидентов. Результаты приведены в таблице 2.

Таблица 2. Результаты исследования алгоритмов балансировки для случая разбиения на 10 резидентов

п	Тип балансировки	Время вычислений, С	Эффективность
2	Без балансировки	1741	0,5
2	Статическая	1025,8	0,962328
2	Динамическая	873,9	0,997158
3	Статическая	664,6	0,782973
3	Динамическая	870,8	0,643395
4	Статическая	547,7	0,7189551
4	Динамическая	870,8	0,4825468

На рис. 3 представлена зависимость эффективности алгоритмов балансировки от типа балансировки для случая сети из двух узлов. Динамическая балансировка в данном случае более эффективна, однако при увеличении узлов наблюдается снижение эффективности динамической балансировки. Это объясняется тем, что в первые моменты времени все резиденты находятся на одном узле и лишь при добавлении сообщений в их очередь происходит перенос вычислений на остальные узлы сети. Этот процесс занимает не- которое время, за счет чего эффективность снижается.

Исследование эффективности алгоритмов балансировки

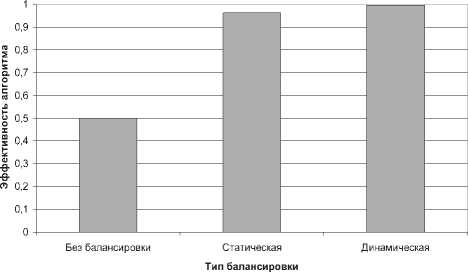
Рис. 3. Эффективность алгоритмов балансировки

Следовательно, необходим комбинированный алгоритм, осуществляющий балансировку перед началом эксперимента и производящий миграцию резидентов в его ходе.

Моделирование комбинированного алгоритма балансировки

Для моделирования случая комбинированного алгоритма балансировки выберем динамическую балансировку и проведем распределение резидентов по узлам сети вручную. Результаты приведены в таблице 3.

На рис. 4 представлены графики, показывающие зависимость эффективности алгоритмов балансировки от конфигурации вычислительной сети.

Таблица 3. Результаты исследования комбинированного алгоритма балансировки для случая разбиения на 10 резидентов

И	Тип балансировки	Время вычислений, С	Эффективность
2	Комбинированная	873	0,9974454
3	Комбинированная	688,1	0,8121242
4	Комбинированная	542,8	0,7190263

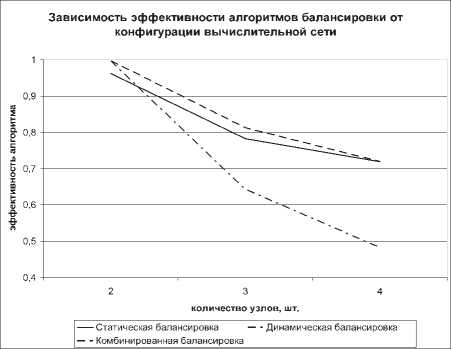
Рис. 4. Эффективность алгоритмов балансировки

Таким образом, эффективность алгоритмов балансировки зависит от разбиения исходной последовательной задачи на подзадачи и соотношения количества вычислительных узлов и подзадач. Алгоритм статической балансировки оказался эффективнее алгоритма динамической балансировки при выбранных условиях экспериментов, что согласуется с известными данными об их функционировании и свидетельствует о работоспособности системы моделирования.

Сравнение различных алгоритмов балансировки. Для сравнения различных видов балансировки сведем результаты экспериментов с использованием статической, динамической и комбинированной балансировок в таблицу 4. Из данных таблицы 4 можно сделать вывод, что комбинированный вид балансировки является наиболее эффективным.

Таблица 4. Сравнение результатов различных видов балансировки, n – число узлов

и	Тип балансировки	Время вычислений, С	Эффективность
2	Без балансировки	1741	0,5
2	Статическая	1025,8	0,9623
2	Динамическая	873,9	0,9972
2	Комбинированная	873,7	0,9974
3	Статическая	664,6	0,7829
3	Динамическая	870,8	0,6434
3	Комбинированная	688,1	0,8121
4	Статическая	547,7	0,7180
4	Динамическая	870,8	0,4825
4	Комбинированная	542,8	0,7190

Заключение

Руководствуясь описанным выше методом имитационного моделирования, была разработана система автоматизации имитационных экспериментов с алгоритмами динамической балансировки нагрузки и произведено исследование работы алгоритмов балансировки на цепи из асинхронно работающих параллельных процессов. Проведенные эксперименты позволяют сделать следующие выводы.

• 1.    Необходим комбинированный алгоритм, осуществляющий балансировку перед началом эксперимента и производящий миграцию резидентов в его ходе.

• 2.    Эффективность алгоритмов балансировки зависит от разбиения исходной последовательной задачи на подзадачи и соотношения количества вычислительных узлов и подзадач.

• 3.    Алгоритм статической балансировки эффективнее алгоритма динамической балансировки при выбранных условиях экспериментов, что согласуется с известными данными об их функционировании и свидетельствует о работоспособности системы моделирования.

В итоге можно сделать заключение о работоспособности и пригодности предложенной системы имитационного моделирования алгоритмов балансировки.