Разработка технологий численного моделирования сопряженных задач газовой динамики и термодинамики композитных конструкций перспективных высокоскоростных летательных аппаратов

аэрогазодинамика, термомеханика, гиперзвук, органопластики), которые в процессе эксплуатации термодеструктируют и подвергаются механической эрозии. Выбор оптимального теплозащитного материала является важной задачей на этапе проектирования летательного аппарата.

Освоение гиперзвуковых скоростей требует проведения комплексных исследований, в которых можно выделить такие составные части, как исследование гиперзвуковой аэродинамики полета и теплообмена на поверхности конструкций гиперзвуковых летательных аппаратов, исследование теплофизики и термопрочности материалов конструкций, разработка новых материалов конструкций, а также проблемы гиперзвуковой аэроупругости, управления и др. Экспериментальные методы исследований этих задач во многих случаях затруднены, поэтому основным инструментом проектировщика является численное моделирование. Задача анализа поведения теплозащитного материала должна решаться в совокупности с задачей газовой динамики для того, чтобы учесть взаимное влияние набегающего газового потока и продуктов терморазложения композиционного материала. Существующие коммерческие пакеты не позволяют решить задачу в такой сложной сопряженной постановке, поэтому необходимо разрабатывать специализированное математическое и программное обеспечение.

Математическая постановка задачи. Рассмотрим процесс обтекания конструкции летательного аппарата, имеющего конусообразную неосесимметричную форму, высокоскорост -ным набегающим потоком. Общая постановка сопряженной задачи аэродинамики и термомеханики состоит из 3-х систем уравнений:

• 1)    уравнений Навье-Стокса внешнего газового потока, обтекающего конструкцию;

• 2)    уравнений внутреннего  тепломассо-

• переноса в конструкции;

• 3)    уравнений термоупругости оболочечной конструкции.

Влияние газообразных продуктов терморазложения и изменения геометрии конструкции вследствие термодеформации на течение внешнего газового потока не учитывается.

• А.    Система уравнений аэротермодинамики

Система уравнений вязкого теплопроводного сжимаемого газа состоит из уравнения неразрывности, уравнений движения и уравнения энергии [1]. Граничное условие на твёрдой стенке, которая является границей раздела газовой и твёрдой сред имеет вид:

v = 0 , 0 = 0 w ,

-XV0 ' n = -Xw V0w ■ n + EgCT^ - Ew^ , где v - вектор скорости, 9 - температура газа, 9w -температура твердой стенки (совпадает с температурой газа на этой стенке), X и Xw - коэффициенты теплопроводности газа и твёрдой поверхности соответственно, 9max - максимальная температура газа в пограничном слое, VOw -градиент температуры со стороны твердой поверхности, eg и ew - интегральные коэффициенты излучения нагретого газа и твердой поверхности и о - коэффициент Стефана-Больцмана.

• B.    Система уравнений внутреннего тепло-массопереноса

Будем рассматривать конструкцию, обтекаемую внешним потоком, изготовленную из композиционного материала на полимерной матрице с термостойкими керамическими волокнами. В матрице такого композита при нагреве до высоких температур, характерных для аэродинамического нагрева, происходят физикохимические процессы термодеструкции, сопровождающиеся образованием газообразных продуктов терморазложения, которые накапливаются в порах материала и отфильтровываются во внешний газовый поток, а также образованием новой твердой фазы - пиролитической фазы матрицы, которая обладает существенно более низкими упруго-прочностными характеристиками, чем исходная полимерная фаза. Четырехфазная модель для описания внутреннего тепломассопереноса и деформирования такого композита имеет вид [2]:

• 1)    уравнения изменения массы полимерной фазы матрицы:

^p b a t     J'

• 2)    уравнения фильтрации газообразных продуктов термодеструкции в порах композиционного материала:

  Sp g ^ g d t

  
  

  ^+V^ g v g = J ^r ;

  
  
  
  

• 3)    уравнения теплопереноса в термодеструк-

• тирующем композите:

d0 _

P c ^f =-^V- q ^- c g ^V0"P g Ф g v g

- J A e 0;

где ф ь , ф д - объемные концентрации исходной полимерной матрицы и газовой фазы; р ь -плотность исходной полимерной матрицы (полагается постоянной); р д - среднее по поре значение плотности газовой фазы (переменная величина); с д - удельная теплоемкость газовой фазы при постоянном объеме, р и c - плотность и удельная теплоемкость композита в целом, q -вектор плотности теплового потока, 9 - температура композита, общая для всех фаз; V g -вектор скорости движения газовой фазы в порах; A e ⁰ - удельная теплота термодеструкции матрицы; J - массовая скорость термодеструкции матрицы и Г - коэффициент газификации матрицы.

К уравнениям (1)-(3) присоединяются определяющие соотношения, связывающие вектор-функции q и V g с функциями V0 и V p с помощью законов Фурье и Дарси, а также соотношение Аррениуса для J и уравнения Менделеева-Клайперона для порового давления газовой фазы р :

q = - л -V0 , р д ф д v g = - K -V p,

I Ea 1

J = J o exp I- r | I , P =

P g R o 0

^M 0 ^,

где J о - предэкспоненциальный множитель, E a -энергия активации процесса термодеструкции, а Л - тензор теплопроводности и K - тензор газопроницаемости композита зависят от концентраций фаз [2].

На нагреваемой части поверхности конструкции граничные условия для уравнений(1)-(3) выглядят следующим образом: р = ре, 9 9w, где ре - местное давление внешнего газового потока на поверхности, а 9w - температура поверхности композита. На остальной части поверхности композита задаются граничные условия герметичности и теплоизоляции: n -Vp = 0, -n - Л-V0 = 0.

C. Система уравнений термомеханики оболочечной конструкции

В криволинейной системе координат O q 1 q 2 q 3 , связанной со срединной поверхностью оболочечной конструкции летательного аппарата, система уравнений термомеханики включает в себя [2]:

• 1)    уравнения равновесия оболочки:

ad : ( A ^{e T}~ ^:d ( A ^a T ) - "A T ^{ee +}

ЙА                  d P,

• ■ , ' Т ав + A a A в k a Q a — A » -    = 0,

a q в                      a q a

^( AeM ™)+^( AaM ae )-^T M вв + aq            aq »v          aqa йа                 ap.

M i» - A a a» Q a - A в Г = 0, a q в                     a q a

• - A , A 2 ( kT + k 2 T 22          + ' ^AQ' - p e A 1 A 2 -

• dqi     dq 2

A α , k α – параметры первой квадратичной формы и главные кривизны срединной поверхности оболочки, α,β = 1,2.

Введены также обозначения для усилий и ˆˆ моментов тепловых напряжений Ta , Ma, зависящих от температурных деформаций Ea оболочки:

(1) E ap^Ep , в=1

h

2 e 3 j ) = j a _{0 2} e ₃ q 3 dq 3 , h /2

^EY = ^{( a}f ф f B Y ^+аь ф ьЦ ^{)( 0-0}o ) ⁺ t

^+aP ^ Y j ^{( 0 (} t ) - ^{0 ( Т ))<} Р P ^{d T} - P p V p ^ Y ,

0                                                         (8)

ˆ a            c

e=1

( j )

^bP   =

(0) ap^bp ,

M a

h j a 01E p q 3 dq 3,

^{-( k} 1 ^{+ k} 2 ) A i A 2 ф д P g = ⁰;                                     (5)

2) кинематические соотношения:

e aa =	1 d U„ α A a 5 q a	+ 1   d A a A 1 A 2 d q p	U p + k a W ,
	1 d W	' 'У    k a U,
2 e α3	A a d q a		α,
2 e 12	1 d U 1 = A 2 d q 2	+± d U 2. _ A 1 a q 1	—L f^ A. и 1 +d A 2. и 2 1 , A 1 A 2 .7 q 2       a q 1     J
Kaa =	=± a/ a, A a 5 q a	+ 1 d A - A 1 A 2 d q p	Y p ,  2 K a3 =- k a Y a ,
2 k 12	= ± dY 1 A 2 d q 2	.+± dY 2 - A 1 a q 1	1 f d A    d A  ) T" Y 1 + t" Y 2 1 ; A1A 2 .d q 2      d q 1    J	(6)

3) определяющие соотношения оболочки:

где α f , α b , α p – коэффициенты теплового расширения волокна, полимера и пиролитической фазы матрицы, β p – коэффициент усадки, B γ , Ω γ – коэффициенты, зависящие от расположения волокон в композите, γ = 1,2,3 [2].

Вследствие размягчения полимерной матрицы и её термодеструкции, жесткости оболочки изменяются при нагреве. Учет этого изменения для ортотропных композитных оболочек осуществляется с помощью 2-х функций a θ 1 , a θ 2 [2]. Деформации ε αβ и напряжения σ αβ в оболочке вычисляются по следующим формулам:

^E ap    e ap ⁺ q 3 ^K ap ,    ^E 33    ⁰,    ^E a3    e a3 ,

^ aa

^{- f} a P ⁺ a 01 E ^C i»

P= 1

^e PP ^{+ q} 3 ^K pp

—

^E p

0 12    a 01 ^C 66 ^{( E} 12 ^{+ q} 3 ^K 12 )’   ^a , P 1,²’

Для поперечного нормального напряжения σ 33 и напряжений межслойного сдвига σ_α 3 имеем следующие формулы [2]:

T aa = Z ( C ap e pp + N ap K pp ) - P ga - T , 0= 1

T 12 = 2( C 6₆ e i2 + N 66 K 12 ),

M aa = E ( N ap e _pP + D . K pp ) - M ga - M a , 0= 1

M 12 = 2( N 6 ₆ e i2 + D 66 K 12 ),

Q a = Ce a3 ;                                    (7)

где T αα , T αβ , M αα , M αβ – усилия и моменты в оболочке; Q α – перерезывающие усилия; e αα , e α 3 , e 12 – деформации срединной поверхности оболочки; κ_αα, κ_α 3 , κ 12 – искривления срединной поверхности; U α , γ α , W – перемещения, углы искривления и прогиб срединной поверхности;

i ( D + D 1 1     (                     ^{0 (0)}A

V p l+ p l Z  £r   Л7(0)р -u^d)^

O33 = 6n ----;----+ TC31 I a01 ell + a01 K11  £1Г

V 2 h VJ

P 1     (                   0 (0)^1      0 (0)^

g1 10      (0)           (1)

, + , C32 I a01 e22 + a01 K22   £2   I , C33 £3

h h VJ

^{+ (} p 2 ^- P i ) ^ ⁽ q 3 ) ^{+ P 1} 2 ^{p 2 +}» g p ,

Wq3) 0   (0)      = wq3) C0

^u 13        ,     ^44 e 13 a 02 , ^u 23        ,     ^55 e 23 a 02 ,

13        h44 13   2       23        h55 232

• ¹     q 3        2 \    ¹ ( q 3 |

^ ( q 3 ) = 7- -y,  n ⁽ q 3 ) = T^- It I ,

• 2    h          4 V h J

где p 1 и p 2 – давления на внешних поверхностях оболочки.

Разработка метода решения сопряженной задачи. Для численного решения

сопряжённой задачи используется пошаговый метод с двумя шагами по времени A 1 1 и A 1 2 . Максимальный крупный шаг A 1 1 по времени используется для изменения граничных условий задачи — входных данных набегающего потока и решения задачи внутреннего тепломассопере-носа. На каждом шаге A 1 1 решение осуществляется в четыре этапа.

Этап 1. Решение системы уравнений внутреннего тепломассопереноса (1)-(3). Это решение осуществляется численным конечно-разностным методом с использованием метода линеаризации и неявной разностной схемы, детали которого описаны в [2]. Температура поверхности конструкции, взаимодействующей с набегающим газовым потоком, на этом этапе полагается известной и берется с предыдущего временного шага A t 1 .

Этап 2. Осуществляется цикл решения системы уравнений Навье-Стокса с мелким шагом A 1 2 до установления потока. Для решения систем дифференциальных уравнений Навье-Стокса используется метод конечных объемов на основе элементов, центрированных относительно узлов сетки (vertex-centered volume) [3].

Этап 3. Осуществляется решение системы уравнений термоупругости оболочечной конструкции аппарата (5)-(7) с помощью метода конечного элемента. Входными данными для этой задачи являются поля давлений на внешней p 1 и внутренней p 2 поверхности оболочки, которые определяются после решения уравнений газовой динамики, а также распределение температуры 9, объёмных концентраций фаз и порового давления p газообразных продуктов терморазложения композитной оболочки, которые рассчитываются при решении уравнений внутреннего тепломассопереноса (1)-(3).

Этап 4. После решения задачи термоупругости осуществляется расчёт термонапряжений в оболочке с помощью формул (9).

Результаты численного решения. В работе представлены результаты численного моделирования обтекания фрагмента корпуса модельного летательного аппарата эллипсоидальной формы гиперзвуковым потоком газа ( M=6) на высоте 15 км [4, 5]. На рис. 1-4 представлены распределения тепловых деформаций 8 1 и £ 3 , порового давления p газообразных продуктов терморазложения полимерной фазы и поперечного напряжения 0 33 вдоль безразмерной координаты по толщине оболочки на нижней поверхности в точке, удаленной от критической на расстояние 30 R , где R - радиус затупления носовой части.

Характерной особенностью функций 81 и 83 является их немонотонность: в зоне повышенной температуры (по толщине оболочки) происходит рост значений тепловых деформаций, однако при переходе через условную точку начала интенсивного терморазложения происходит уменьшение тепловой деформации, обусловленное образованием пиролитического остатка. График распределения азз показывает, что в подповерхностном слое после начала терморазложения полимера возникает значительный максимум напряжения, обусловленный ростом порового давления газообразных продуктов термодеструкции, а также возникновением усадочных деформаций. Значения поперечных напряжений на нижней части оболочки достигают значений в 0,13 ГПа, что значительно превышает предел прочности композитной оболочки в поперечном направлении. В результате, в этой части оболочки может возникнуть разрушение по типу расслоения, при котором верхние слои ткани композита отслоятся от остальной части материала. Аналогичное явление может произойти и на верхней части оболочки, поскольку поперечные напряжения начинают расти и достигают значений в 0,06 ГПа, что хотя и меньше значений в нижней части оболочки, но также сравнимо с пределом прочности материала в поперечном направлении.

Исследование выполнено при поддержке гранта Президента РФ МК-3007.2015.8.

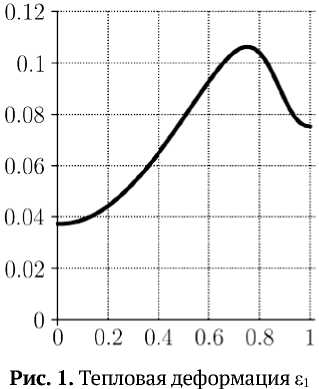
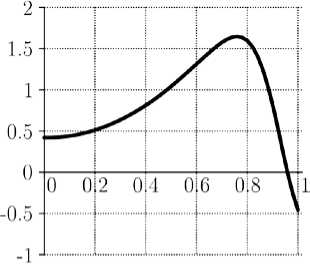
Рис. 2. Тепловая деформация 8 3

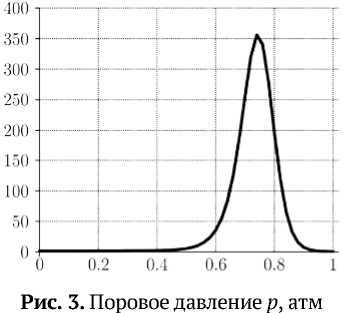
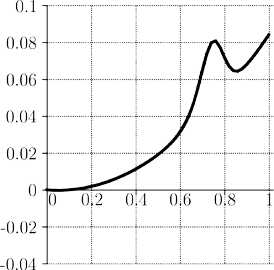
Рис. 4. Поперечное напряжение σ 33 , ГПа