Разработка тепловой математической модели для диагностики полимерных композиционных материалов, применяемых в авиастроении в условиях нестационарных температур

В авиации полимерные композиционные материалы (ПКМ) очень часто эксплуатируются в условиях нестационарных температур. Поэтому возникает вопрос о проверки соответствия материалов условиям эксплуатации. Основные преимущества углеродных ПКМ состоят в высокой теплостойкости, малой плотности, стойкости к тепловому удару и облучению. Они длительное время могут работать при температурах до 773 °К в окислительной среде и 3273 °К – в инертной среде и вакууме. При этом их прочность с ростом температуры повышается в 1,5 – 2 раза.

ОПИСАНИЕ ЗАДАЧИ

Для проведения всесторонней диагностики свойств ПКМ, требуется рассмотреть тепловую модель, описывающую поведение ПКМ в условиях нестационарного нагрева. По своим структурам ПКМ большинство материалов состоят из некоторого числа слоев, поэтому интерес представляет поведение температуры как внутри слоя, так и внутри самого материала. Основны-

ми параметрами образца ПКМ являются б - диэлектрическая проницаемость и tg 5 - тангенс угла потерь.

ПУТИ РЕШЕНИЯ ЗАДАЧИ

Исследуемый материал подвергается одностороннему нестационарному нагреву, вследствие которого образуется неравномерное распределение температуры нагрева диагностируемого образца по толщине. Запишем уравнение теплопроводности с целью получения выражения описывающего распределение тем- пературы нагрева по толщине.

Для упрощения описательного процесса рассмотрим один слой, который будет являться базовым элементом для многослойной модели. Слои между собой будут сшиваться через гра- ничные условия температур на их поверхности. Границы раздела слоем могут быть реальными или условными.

Будем считать, что температура в каждой точке (x, y, Z) образца ПКМ в момент времени t описывается функцией Т(x, y,z). В начальный момент времени (t = 0) все части тела имеют одинаковую температуру (температуру тела в нормальных условиях). Для решения поставленной задачи составим теплофизическое уравнение для образца ПКМ, считая, что об- разец-тело однородное по толщине и не имеет на поверхности изломов, трещин, ребер и т.д. В случае наличие различных неоднородностей температурный рельеф будет отличен в местах неоднородностей.

Уравнение распространения тепла в произвольном объеме V, ограниченный гладкой поверхностью S, можно представить в виде не- скольких слагаемых [1,2]:

• 1)    Изменение количества тепла в объеме V за промежуток времени ( t 1 , t )

²               dT

Q_y = -J dt JJ k ( x , y , z )— dS ,    (1)

dn t S где k – коэффициент внутренней теплопроводности, n – внутренняя нормаль к поверхности S,

Т – температура нагрева тела.

• 2)    На изменение температуры объема на A T за промежуток времени A t надо потратить количество тепла

t ат

Q., = J dt JJJ yp — dV ,      (2)

t1    V dn где у(x, y, Z) - теплоемкость вещества, p(x, y, Z) - плотность вещества.

• 3)    Функцией F ( x, y, Z ) обозначим плотность тепловых источников находящихся в теле (количество выделяемого тепла в единицу времени в единицу объема). Количество поглощенной или выделяемой энергии за промежуток времени ( t i , t 2 ) равно

t

Q3 = J dt JJJ F (x, y, z) dV,(3)

Полный баланс энергии для заданного объема будет представлен в виде:

Q2=Q1+Q3.(4)

J ^dtH J"yP ^^dv = -j dtjjk ⁽ x,y,z ) ^dS +

; v ^п t sdn t2

+ J dt JJJ F ( x,y,z ) dV

• t i V

Применив для второго интеграла теорему Остроградского, в целом получили уравнение теплопроводности для неоднородного изотропного тела.

YP— = div ( kgrad- ) + F ( x , y , z , t ) . (5) dt

Будем считать, что тело однородное и пара-

метры /, p и k = const d-   2f d2 - d2 - d2 - )

= a +    + dt     ^ dx2   dy2   dz2 v

+ f ( x , y , z , t ) . (6)

k               \ F ( x , y , z , t )

где a = — ; f ( x , y , z , t ) =

\ YP                   YP

По теории теплопроводности для нахожде- ния температуры внутри тела в любой момент времени необходимо знать начальное условие и граничное условие (тепловой режим на границе тела).

Граничные условия могут задаваться разными способами в зависимости от того, что известно. Граничные условия на поверхности тела обычно задается тепловым потоком q

, d- q = - k ;                  (7)

dn или в каждой точке на поверхности тела задается температура -^ = f (S, t) - известная функция точки на поверхности и времени.

Начальные условия это распределение температуры по толщине тела.

^- 1 , = о = ^ ( ^{x ,} У ^{, z} ) .               ⁽⁸⁾

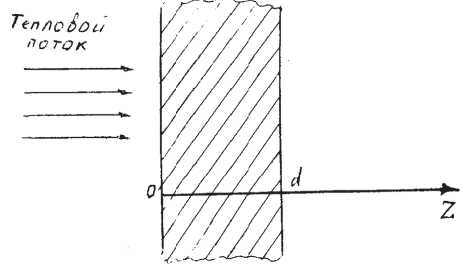
Будем считать: нагрев производится СВЧ энергией, для связывания в единую систему электродинамические модели ПКМ и тепловую модель; тепловой поток производящий нагрев распространяется вдоль одной координаты (координаты z см. рис. 1), перпендикулярной поверхности тела, вглубь тела. Вследствие этого будем считать, что распространения тепла по двум другим координатам не происходит и температура нагрева тела имеет распределение только по координате z. В силу сделанных утверждений можно перейти от решения трехмерной задачи теплопроводности к решению одномерной.

Для решения поставленной задачи потребуется уточнение характеристик условий нагрева и физического процесса нагрева. Для простоты описания будем считать:

• -    излучение монохроматическое (источник нагрева –электромагнитная волна);

  - состояние тела равновесное, перенос тепла

осуществляется за счет теплопроводности;

• -    теплоотдачей всех видов пренебрегаем, в силу быстротечности процесса нагрева;

• -    для исследуемого материала берется модель неограниченной пластины (рис.1) [3,4].

Решение уравнения теплопроводности бу- дем производить в духе электродинамики. Нагревательная энергия, которая поглощается об- разцом ПКМ будет равна:

P = погл 2 Z e-a

где E ₀ – напряженность электрического поля, производящего нагрев импедансного тела;

Z _c – импеданс исследуемого тела, определяемый как

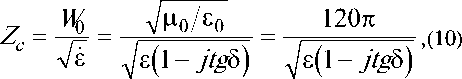
a - коэффициент затухания электромагнитной волны в импедансном теле

где

Рис. 1. Модель неограниченной пластины

имеет вид (12) и будет искаться через фундаментальную функцию:

T ( z, t ) = T 0 + T^ ,        (15)

₁ d          ( zs ) ²

T 0 =---- 7= I" ф^z ) e ⁴ a ² t d^ ,      (16)

2 a V nt q

T нагр

t d 2^             1                ⁽ z - )

[[- E ⁰-- A----- e ⁴a ²⁽ t ^-T ) e -^{2a ( z}- ^- ) d - d T

" о " о ²| Z_c I к 2 a n ( t - T )

α= 2 π f ^{ε a µ a} 2

где

µ _a = µ ₀ , ε _a = ε ₀ .

( 1 + tg ² δ - 1 ) ,   (11)

Выражение (16) представляет собой распределение начальной температуры тела по его толщине. Численное решение выражения (16)

приводится ниже.

Теперь составим одномерное уравнение теплопроводности для ПКМ образца, считая, что температура нагрева (избыточная температура) распространяется только вдоль одной координаты (координаты Z).

T

¹ 0

1           - ( £ - -£

Ф о ^{( z ) e 4} a ² '

V n

d

.

dT dTT 1 E 2 ,, — = a--1---— e Z dt dz cy 2|Zc|

Т - избыточная температура, T = Т _{наг p} - T , ;

a ² - коэффициент температуропроводно-

2 К . сти, a = — ;

с у

ℵ – коэффициент теплопроводности;

c – теплоемкость;

γ – плотность вещества;

t – Время облучения (нагрева) материала;

z – координата распространения электромагнитной волны, 0 ≤ z ≤ d ;

d – толщина ПКМ образца.

Это типичное уравнение теплопроводности, в котором первый член в правой части отвечает за количество тепла прошедшее путем теплопередачи через границу перпендикулярную плоскости ХY. Второй член правой части отвечает за количество тепла поглощенное материалом за время облучения.

Для конкретного решения уравнения теплопроводности (1) необходимо уточнить начальные и граничные условия.

Начальное условие: задается начальная температура по всей поверхности материала, в данном случае

Т _наг p ( z ,о ) = ф ₀ ( z ) = T q или T ( z ,0 ) = _{V 0} ( z ) = 0 . (13)

Граничные условия: без учета теплоотдачи нагреваемого тела применяются граничные условия второго рода dT   .     E2 dT

, (^0, t ) = ^- ./к-^: t⁽ d ’ t ) = ⁰ ,        ⁽¹⁴⁾

dz          2 Z c |K dz

Решением уравнения (13) в общем виде [1,2]

Выражение (18) показывает распределение начальной температуры тела по толщине непосредственно перед началом исследуемого нагрева.

Распределение избыточной или нагреваемой температуры по толщине имеет вид (17) ниже приведено численное решение:

T,

нагр

¹¹   E О

V n 2 a 2| Z c I

e

, ( z -- ) ²

4 a ² ( t —T ) e -2 a ( z -- )

t

. (19)

Выражение (19) качественно показывает дискретный прирост температуры нагрева по толщине тела и по времени нагрева.

Задавшись дискретами по толщине и по времени мы получаем временное распределение приращенной температуры по толщине образца ПКМ. Точность вычисления температурного распределения будет зависеть от точности выбранного численного метода, и от шага дискретов по толщине и времени.

Полученные результаты справедливы для поглощающих материалов, для полупрозрачных материалов математическая модель будет представлена как поглощающей, рассеивающей и испускающей. По этому в математической модели для полупрозрачных материалов необходимо рассматривать процессы рассеивания, испускания и переноса энергии [5].