Разработка вычислительного алгоритма реконструкции объемных изображений в рентгеновской компьютерной томографии с применением голографических методов

В работах [1–8] рассматривались различные подходы получения фазоконтрастных изображений некоторых слоев объекта исследования в рентгеновских лучах, используя физические основы отражения и преломления по принципам Лауэ и Брэгга. В этих работах также проводится попытка связать фазоконтрастные изображения с голографическими. Однако разработка метода получения внутренней структуры в любой точке объекта по фазоконтрастным изображениям (проекциям) не была достигнута.

В работах [9–11] была сформулирован задача реконструкции внутренней структуры сечений объекта в фазоконтрастной рентгеновской томографии (показатель преломления) на основе трехмерного преобразования Радона (для микрообъектов).

Фазоконтрастные изображения могут быть получены применением осевой голографии по

Информатика и вычислительная техника принципу Габора [12, 13]. Для иллюстрации этого принципа рассмотрим облучение объекта монохроматическим когерентным рентгеновским лучом (рис. 1).

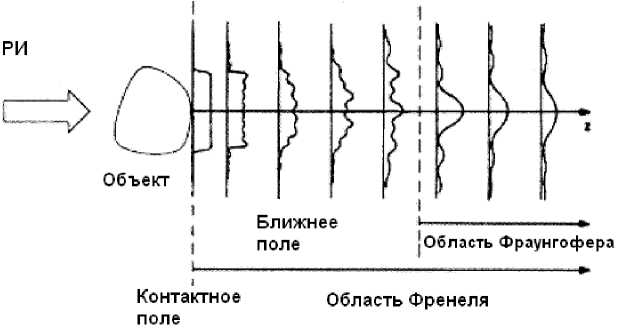
Рис. 1. Принцип когерентного получения изображений

Абсорбционно-контрастное изображение наблюдается на плоскости, контактной с объектом. Фазоконтрастные изображения наблюдаются в ближнем поле области преломления Френеля.

Чистый контраст поглощения, который используется в традиционной КТ [14], наблюдается только в плоскости, контактной со снимком (то есть когда расстояние между объектом и плоскостью изображения является нулевым. Фазовый контраст из-за дифракции рентгеновских лучей происходит на всей области дифракции Френеля.

Поэтому, для того чтобы получить фазоконтрастное изображение, достаточно отодвинуть детектор от объекта.

Основные соотношения по решению обратной голографической задачивнутренней структуры объекта

Теория [9–11], основанная на фундаментальном отношении между трёхмерным (3D) преобразованием Радона функции объекта и двухмерным (2D) преобразованием Радона фазоконтрастной проекции, дает возможность решения обратной голографической задачи по визуализации внутренней структуры объекта с применением алгоритмов реконструкции изображений классической рентгеновской компьютерной томографии. Вводятся базовые основы когерентного построения изображений, выводится формула, описывающая линейное отношение между фазовой функцией и яркостью в ближней зоне дифракции Френеля.

Введем декартову систему координат относительно объекта исследования ( x 1 ,x 2 ,x₃ ) (рис. 2).

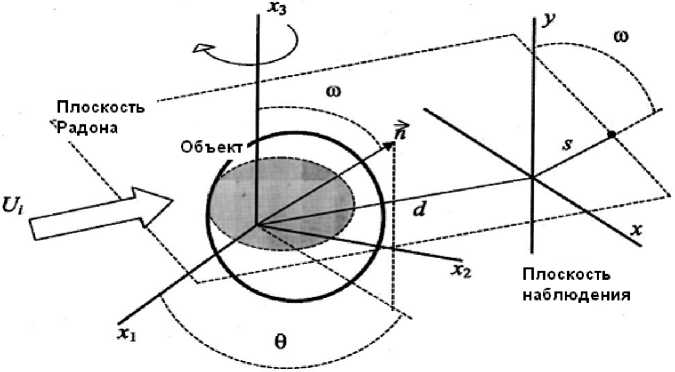
Рис. 2. Координатная система для объекта и плоскости наблюдения

Детектор снабжён собственной системой координат ( x , у ) , основание которой лежит в плоскости ( x 1 , x 2 ) , а направление оси у совпадает с направлением оси х₃ .

Смешанный фазо-амплитудный объект можно описать коэффициентами линейного поглощения р(x1,x2,x3) и функцией f (x1,x2,x3) = n(x1,x2,x3)-1, где n(x1,x2,x3) представляет дей- ствительную часть показателя преломления.

Мы полагаем, что монохроматическое когерентное волновое поле с длиной волны X облучает объект в направлении, определённом углом обзора 6 .

Реализация подобной геометрии может быть достигнута вращением объекта вокруг оси x ₃ .

Поток поля монохроматической волны объекта можно описать следующим образом:

U б ( x , у ) = Т б ( x , у ) U i ,                                                                                (1)

где U i - плоская монохроматическая волна после взаимодействия; Т б ( x , у ) - комплексная функция передачи объекта на угле 6

T 6 ( ^x , У ) = M 6 ( ^x , У ) ^ex P ^[ i Ф е ( ^x , У ) ]

с модулем M 6 ( x , у ) = exp

^- 1 Н б ( ^x , у )

, где

p₆ ( x , у ) = j p ( x 1 , x 2 , у ) S ( x - x 1 cos 6- x ₂sin 6 ) dx 1 dx 2 ,

R ²

и фазовая функция

2П

Ф₆ ( x , у ) =— f ( x , x ₂, у ) S ( x - x cos 6- x ₂ sin 6 ) dx_xdx^ .                                    (3)

X

R ²

Следует учесть, что выражения (2) и (3) описывают двухмерное преобразование Радона в плоскости, перпендикулярной оси x ₃ . Распределение яркости на расстоянии z от объекта может быть представлено следующим образом:

1 6 ^Z ( x , у ) = \h_z ** U 6 \2 ,                                                                                     (4)

где

h ( x,_y ) = exp^ ikj ) i X z

■ П / 2     2\

exp ixz(x +у )

– функция распространения Френеля; двойной звёздочкой обозначена двухмерная свёртка, при

.   2п этом к = —

.

X

Задачей восстановления является нахождение функции f (x1, x2, x3) по измеренным значени- ям 16z (x, у), 0 < 6 < п . Чтобы найти аналитическое решение этой задачи, сделаем некоторые приближения, которые будут соблюдаться в ближнем поле Френеля. Сначала произведём преобразование Фурье для функции распределения Френеля:

Hz (^,n) = exp(ikz)exp [-inXz(^2 +р2)], где ^ и n являются пространственными частотами. Для малых Xz частотное представление функции может быть упрощено:

Йz (^,n) = exp(ikz)[1 - inXz(^2 +n2)], где мы сохранили только линейные части ряда Маклорена для экспоненциальной функции. Таким образом, яркость на малом расстоянии z становится равной

1 6 z ( x , у ) ” ( 1 + i ^X z V ² I U 6

,                                                                                       (5)

где V ² - лапласиан.

Информатика и вычислительная техника

При незначительном изменении показателя поглощения объекта ц₆ ( х , у ), что соответствует для малоконтрастных объектов, распределение яркости на значительно малом расстоянии d от объекта определится следующим образом:

16d (х, у ) = 160

¹ -Ц х , у ) .

По своему происхождению равенство (6) описывает распределение яркости в ближней зоне Френеля, где X z <<  , ’—.

-2 +п2

Равенство (6) устанавливает линейную связь между фазовой функцией и измеренной яркостью (яркостью на детекторе).

Использование равенства (6) для представления яркости помогает установить прямую связь между данными яркости и искомой функцией f ( х 1 , х ₂, х 3 ) объекта, которую необходимо восстановить. Для этого требуется преобразование Радона, которое будем применять дважды: в плоскости х-у и в трёхмерном пространстве ( х 1 , х ₂, х 3 ) . В первом случае мы имеем дело с двухмерным преобразованием Радона, во втором случае – с трёхмерной версией преобразования Радона.

Двухмерное преобразование Радона можно представить, как

R ₂ ( s , ю ) = J g ( х , у ) 8 ( s - х sin ю- у cos to ) dхdy .

R ²

Оно описывает интегрирование функции g ( х , у ) по линиям, определённым равенством х sin ю + у cos ю = s в плоскости х-у , тогда как трёхмерное преобразование Радона

R 3 ( s , 6 , ю ) = J f ( х 1 , х 2 , х з ) 5 ( s - ( х 1 cos ю + х ₂ sin ю ) sin ю - х ₃ cos ю ) dх₁ dх ₂ dх ₃ R ³

описывает интегрирование функции f ( х 1 , х ₂, х ₃ ) по плоскостям. Такая плоскость перпендикулярна единичному вектору n = ( cos 6 sin to ,sin 6 sin to ,cos ю ) и имеет расстояние s до исходной плоскости облучения объекта (см. рис. 2).

Мы можем сформулировать следующий результат.

Пусть gе(х, у ) =16d (х, у ) /160 (х, у)- 1, где I6d (х, у) - яркость распределения на малом расстоянии d.

Яркость в плоскости, контактной с объектом, равна 160 = |М6 (х, у)Ui |2, тогда д2

—у R з (s, 6, ю) = — R 26 (s, ю).

дsd

Общий алгоритм реконструкции фазоконтрастных томографических изображений внутренней структуры объекта

Используя выше представленные соотношения, можем вывести алгоритм реконструкции.

Функцию объекта можно найти по формуле (8), если обратить трёхмерное преобразование Радона.

Точная обратная формула трёхмерного преобразования Радона, открытая Радоном [14], выглядит следующим образом:

1 п         п     д 2

f ( х ], х ₂, х ₃) = —- Jsin ю d ю| d 6—- R ₃ ( s , 6 , ю ) , 4 п ² 0        0    ^д s ²

где, выполняя дифференцирование, s заменяется следующей формулой s' = (х1 cos 6 + х2 sin 6) sin ю + х3 cos ю.

Примечательным фактом является то, что эта формула применяет вторую производную к преобразованию Радона. Это значит, что, подставив выражение (8) в формулу (9), мы сразу перейдём к формуле f ( x1, x 2, x3 ) =

1 П          П

-----z- j sin ю dю[ d 0 R 20 (5', го), d4n 0        0

которая представляет решение задачи восстановления фазоконтрастной КТ.

Формула (10) предполагает, что двухмерное преобразование Радона в плоскости x–y должно быть просчитано для каждой двухмерной проекции ge (x, y). Затем этот результат восстанавли- вается в трёхмерном пространстве, используя при этом оператор восстановления трёхмерного обратного преобразования Радона. Следует учесть, что эта формула является устойчивой, так как все используемые операторы являются непрерывными и не требуют дифференцирования.

Формула (10) не имеет каких-либо особенностей и может непосредственно использоваться в численной реализации алгоритма восстановления. Тем не менее применение двухмерного преобразования Радона к каждой угловой проекции потребует больших вычислений. Чтобы ускорить эти вычисления, можно использовать быстрое преобразование Фурье. В то же время можно получить более практический алгоритм восстановления, если упростить формулу (10), вычислив интеграл по углу ю. Затем нам следует объединить вычисление двухмерного преобразования Радона и восстановления по углу ю на каждом единичном шаге алгоритма. Чтобы проделать это, для начала перепишем формулу (10), подставляя выражение преобразования Радона для данных gо. Это даст нам f (x1,x2,x3 ) = ,,’ 2 d 4п2

П

П

j d e j J g e ( x , У ) dxdy j 5 ( ( x 1 cos 0 + x 2 sin 0 - x ) sin ю + ( x 3 - У ) cos ю ) sin ю d ю . (11)

Интеграл по углу ю может быть выражен умножением и делением интеграла на выражение ( x 1 cos e + x 2 sin e - x ) ² + ( x ₃ - y ) ².

Пусть i x cos e + x-) sin e - x

Y = tan —--------2--------, x3 - У тогда x-, - y                   .              x cos e + x^ sin e - x cos у = .                  3                        , sin у = .         1          2                     .

J ( x 1 cos 0 + x ₂sin 0- x ) + ( x ₃ - y )            J( x 1 cos 0 + x ₂sin 0- x ) + ( x ₃ - y )

Затем, применяя формулу 5(a(b)) = 5(b-b')/|(da/db)(b')|, которая представляет дельта функцию 5(a(b)), и, используя корень b' уравнения а(b) = 0, получим:

П j 5 ((x1 cos 0 + x2 sin 0 - x)sin ю + (x3 - y) cos ю) sin юdю =

П

H sin у sin ю + cos у cos ю ) sin ю d ю = ¹ ( x^ cos e + x ₂ sin e- x ) + ( x ₃ - y ) 0

1                           ^Л

= ,                                    j 5(cos (ю - у)) sin юdю =

( x 1 cos e + x ₂sin о- x ) + ( x ₃ - y ) 0

1 ^П

• =-------------,                                    j 5 (cos (ю - ю')) sin ю d ю =

|sin(ю'-Y)|-\/(x1cos0 + x2sin0-x) +(x3 -y) 0

• =_________________ I ^x 3 ^- y| _________________

( x 1 cos 0 + x ₂ sin 0 - x ) 2 + ( x ₃ - y ) 2

, П где мы использовали ю = y + —.

Информатика и вычислительная техника

Подставляя значение интеграла в (11) и используя

q(x,y)=2- 2, x + У можем записать

1 ⁿ

f ( x1, x 2, x3 ) = TT^ dd 6 g 6, 4n2 d в котором, следуя свёртке, аргументы x и у функции q **g6 (двухмерная свертка) заменяются соответственно на x = x1cos 6 + x2sin 6 и у = x3. Равенство (12) представляет алгоритм восстановления в форме фильтрующего восстановления.

Этот интеграл свёртки можно рассчитать в области Фурье, что также позволит сократить время вычислений применением быстрого преобразования Фурье. Соответствующая функция фильтра Q(^, п) может быть найдена применением двухмерного преобразования Фурье к ядру свёртки q (x, у), что даст

Q (^)=И т У? x + у

exp [-i 2п( x ^ + у ^]dxdy = 2 j exp (-у |^|) exp (-i 2пуп) dy = Qа (^, п) =

^1

^2 +п2"

Функция фильтра Q ( ^ , п ) имеет бесконечно много нулей вдоль линии ^ = 0 и единственный полюс в начале координат. Чтобы точно аппроксимировать полюс на дискретной решётке, мы должны использовать малый интервал дискретизации в частотной области. Этого можно достичь, обнулив дискретные наборы данных, что является стандартным способом решения схожих проблем в восстановлении традиционной КТ.

Дискретная функция фильтра показана на рис. 3.

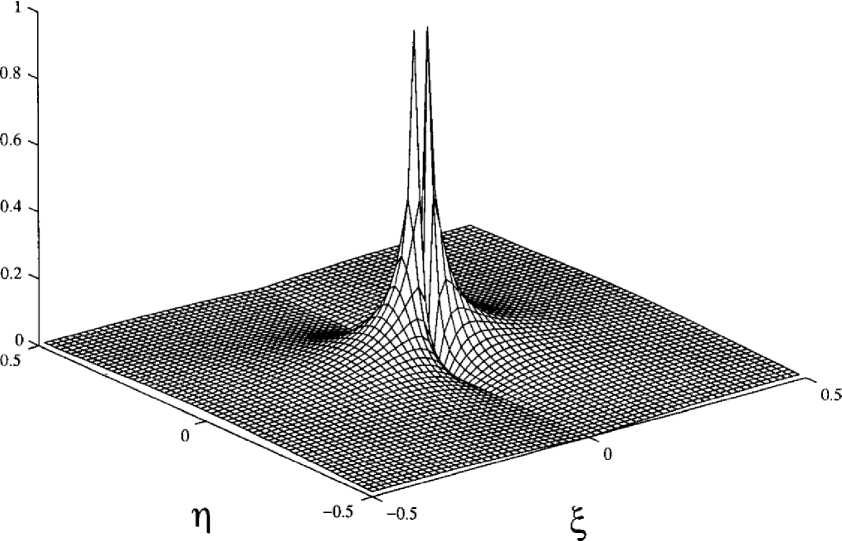
Рис. 3. Нормализованная дискретная функция Q ( ^ , п ) фильтра восстановления

Следует учесть, что Q ( ^ , п ) является функцией переноса низкочастотного фильтра, и поэтому не требуется дополнительной регуляризации для подавления высокочастотных компонентов зашумлённых данных.

Вычислительный алгоритм реконструкции фазоконтрастныхтомографических изображений внутренней структуры объекта

Определение искомой функции показателя преломления f ( x 1 , x 2 , x₃ ) определяется формулой (11)

f ( x 1 , x 2 , x 3 ) =

d 4 n ²

П                      П

j dOjj g 0 (x, у) dxdy j§((x1 cos 0 + x 2

sin 0- x) sin го + ( x3

- у) cos rn) sin гоdго,

П где j 5((x1 cos O + x2 sin O - x) sin го + (x3 - у) cos го) sin гоdго будет равен yn

,учитывая, что x = x1cosO + x2sinO, у = x3 и го =го + —. x2 + у22

Формула (11) примет вид

• 1

  
  

f ( ^x 1 , ^x 2 , ^x 3 ) = —— I d ^O| I g O ( ^x , y ) —---- dxdy . d 4 n ² 0              x ² + у

Рассмотрим выражение (13).

• 1.    В формуле (13) двойной интеграл представляет двухмерную свертку функции g ₀ ( x , у ) и яд- ^y

ра свертки        .

x ² + у

Двухмерную свертку можно определить через двухмерное преобразование Фурье, используя двухмерное быстрое прямое преобразование, а затем обратное преобразование (БПФ):

• а)    двухмерное преобразование Фурье функции J ^ будет Q ( £ , р ) = ' ^ | ;

x ² + у ^{2                   7} 2 +n ²

• б)    определение функции g O ( x , y ).

Вариант 1. Имеется слабоконтрастный объект, у которого коэффициент поглощения р ( x , у ) изменяется незначительно.

Тогда яркость на детекторе при сканировании объекта I O d ( x , у ) определяется по формуле (6), как

I o ^d ( x , y ) = I O ⁰ 1 ~ v4( x , у )

где У ² ф₀ ( x , у ) - лапласиан фазовой функции ф₀ ( x , у ) .

Подставляя последнее выражение в (7), получим

g о(x, у ) = -Xd v 2Фо(x, у ),                                                                 (14)2П где фазовая функция ф0 (x, у) определяется, как

2п ф6(x,у) = — I f (x,x2,у)8(x-xcos0-x2sin0)dx-dx^ .

X

R ²

Моделирование g ₀ ( x , у ) проводится по формуле (14).

Вариант 2. Общий случай: имеется любой объект, у которого коэффициент поглощения р ( x , у ) изменяется каким-либо образом.

Тогда g о ( x , у ) определяется по формуле (7), как g ₀ ( x , у ) = 1 ₀ d ( x , у ) / 1 ₀ ⁰ ( x , у ) - 1, где 1 ⁰ ( x , у ) -яркость на детекторе после объекта при z = 0, т. е. детектор соприкасается с объектом, а 1 0 ( x , у ) -яркость на детекторе после объекта, находящегося на расстоянии z = d от детектора.

1 0 ? ( x , у ) и 1 0 ( x , у ) определяются экспериментальным путем при измерении яркости на детекторе в каждой его точке (пикселе) с координатами ( x , y ) при каждом значении угла поворота объекта 0 .

Информатика и вычислительная техника

Моделирование g ₆ ( x , y ) по формуле g ₆ ( x , y ) = 1 ₆ ⁶ ( x , y ) / 1 ₆ ° ( x , y ) - 1 требует моделирования яркости 1 6 (x , y ) и 1 6 ( x , y ). Для моделирования значений яркостей 1 ° ( x , y ) и 1 6 ( x , y ) можно воспользоваться формулой 1 ₆ z ( x , y ) = | h z * *U ₆12 .

Функцию распределения Френеля h z можно представить через фурье-образ

Hz (^,n) = exp(ikz)[1 - inXz(^2 + п2)], k = 2^ •

Поток волнового поля U 6 ( x , y ) полностью определяется комплексной функцией передачи объекта T ₆ ( x , y ) , которая, в свою очередь, определяется, как

T6 (x, y) = M 6 (x, y) exP [ i Ф6 (x, y)], где

M 6 ( x , y ) = exp

^- 2 M ^x , y )

ц₆ ( x , y ) = J p ( x 1 , x 2 , y ) S ( x - x 1 cos 6- x ₂sin 6 ) 6x 1 dx ₂,

R ²

2n

Ф₆ ( x , y ) = — I f ( x , x ₂, y ) 8 ( x - x cos 6- x ₂ sin 6 ) dx-faz ;

X

R ²

• в)    полученное в варианте 1 или варианте 2 двухмерное преобразование Фурье g ₆ ( x , y ) обозначим ^ 6 ( ^ , п ) .

• 2.    В формуле (13) интеграл J B ₆ ( x , y ) d 6 можно определить любым из известных методов.

Умножим его на Q ( ^ , п ) , возьмем от произведения G ₆ ( ^ , п ) Q ( ^ , п ) двухмерное обратное преобразование Фурье, результат будет равен    g ₆ ( x , y ) | y | dxdy , формула (13).

x ² + y ²

Обозначим этот двойной интеграл как B _е ( x , y ).

п

Вычислительный эксперимент

Реализация вычислительного алгоритма осуществлялась в среде MATLAB, которая эффективно осуществляет матричные вычисления интегралов, дифференциалов, прямого и обратного одномерного и двухмерного преобразования Фурье, одномерной и двухмерной свертки, одномерного и двухмерного преобразования Радона с задаваемыми одномерными, двухмерными и трехмерными матрицами переменных.

Для того чтобы оценить подход, использовалась модель фантома (рис. 4). Фазовый объект был представлен в виде цилиндра диаметром 300 мкм и высотой 300 мкм, диаметр вставок 30 мкм.

Рис. 4. Компьютерная модель фантома. Показаны пять его сечений

Значения яркости серо-белого для объекта были –5·10–7 для цилиндра и –10·10–7, –4·10–7 и –2·10–7 для вставок.

Значения яркостей I ° ( x , y ) и 1 6 ( x , y ) моделировались по варианту 1 вычислительного алгоритма.

Длина волны была принята равной λ = 0,1 нм, размер пикселя детектора – Δ = 0,1 мкм.

Параметры переменных для реконструкции изображений:

– угол сканирования объекта θ изменялся 0 ≤ θ ≤ π с дискретностью Δθ = 0,5°, т. е. было сделано 360 проекций;

– матрица восстанавливаемого изображения 512 × 512 пикселей;

• –    центр изображения находится в центре координат xOy , размер изображения по горизонтали

  (по оси x ) равен 512 пикселей ( ± 256 пикселей), т. е. каждый пиксель изображения равен 300/512 мкм

  
  

  размера объекта, количество пикселей детектора в одном 300/512/0,1 = 3000/512. Параметр x изменяется с дискретностью Δ x = 300/512 мкм, т. е. с дискретностью 3000/512 пикселей детектора;

• –    аналогично по параметру y .

В вычислительном эксперименте были смоделированы фазоконтрастные данные на расстоянии d = 3 см от объекта. Для одного из сечений объекта результаты представлены на рис. 5, где показаны значения яркости между 0,7 и 1,1.

Структуры на рис. 5 появляются в результате фазового контраста.

Восстановленные изображения с параметрами реконструкции, указанными выше, показаны на рис. 6. Для восстановления сечений объекта по формуле (13) использовался разработанный авторами реконструктор томографического изображения [14, 15].

пикселе изображения равно

Рис. 5. Яркость данных 1 ₀ z ( x , y ) для одного из сечений объекта при d = 3 см

Рис. 6. Восстановленные сечения объекта

Сравнивая изображения на рис. 4 и 6, можно видеть, что предлагаемый метод восстанавливает изображение достаточно хорошо.

Выводы

• 1.    Проведено усовершенствование теории и алгоритма фазоконтрастной компьютерной томографии [9–11]. Рассмотрены варианты восстановления изображения для слабоконтрастных объектов и общий случай – для любых объектов. Более детально рассмотрены алгоритмы реконструкции фазоконтрастных томографических изображений внутренней структуры объекта для практической разработки программных реконструкторов.

• 2.    Установлена связь между трёхмерным преобразованием Радона функции преломления объекта и двухмерным преобразованием Радона фазоконтрастных проекций, отражающих соотношение яркости на детекторе в ближней зоне Френеля (размер объекта гораздо меньше λ z ) и яркости на детекторе в зоне поглощения ( z = 0). Эта связь дает возможность осуществить реконструкцию фазконтрастных изображений томографическими методами, принятыми в рентгеновской КТ.

• 3.    Моделирование объекта и фазоконтрастных проекций, последующая реконструкция по ним фазоконтрастных томографических изображений томографическими методами показало хорошую схожесть результатов. При реконструкции использовался разработанный авторами реконструктор томографического изображения.

• 4.    Разработан компактный алгоритм реконструкции фазоконтрастных томографических изображений для экспериментальных установок по исследованию малоразмерных биологических объектов, когда для получения фазоконтрастных проекций осуществляется два массива измере-

• Информатика и вычислительная техника

• 5.    Практическое применение разработанного подхода в получении фазоконтрастных томографических изображений томографическими методами может найти там, где требуется более высокое разрешение на изображении, чем при применении классических методов КТ.

ний: измерения яркости от объекта на детекторе в ближней зоне Френеля и измерения от объекта на детекторе в зоне поглощения.