Разрешение фазовой неоднозначности на основе инерциальных измерений в угломерно-дальномерной сверхширокополосной локальной навигационной системе

В настоящее время большинство навигационных задач можно разделить на две составляющие: позиционирование в открытом пространстве и позиционирование внутри замкнутых пространств. Второй тип задач характеризуется тем, что прием сигналов глобальной навигационной спутниковой системы [1] затруднен, и, как следствие, невозможно обеспечить требуемую точность определения координат потребителя. В связи с этим за-

Разрешение фазовой неоднозначности на основе инерциальных измерений ...

Петухов Никита Игоревич

дачи позиционирования в помещениях решаются при помощи локальных навигационных систем (далее – ЛНС) [2], основанных на различных технологиях. Особенностью ЛНС является необходимость развертывания и поддержания инфраструктуры навигационных опорных точек, что возможно в большинстве практических случаев. Выбор конкретной системы определяется целесообразностью применения той или иной технологии для решения конкретных задач позиционирования.

Насколько известно авторам, наиболее популярными решениями для позиционирования внутри помещений являются:

• •    оптические системы;

• •    ультразвуковые системы;

• •    узкополосные радиостанции;

• •    СШП-радиосистемы;

• •    инерциальные системы;

• •    системы одометрии;

• •    магнитометрические системы.

Одним из наиболее перспективных решений в этой области считаются сверхширокополосные (далее – СШП) радиосистемы [3–5], поскольку они обладают наибольшей потенциальной точностью.

В данной работе рассматривается СШП ЛНС с угломерно-дальномерной архитектурой [6–9] (см. Рисунок 1). В ее основе лежит фазовый радиоинтерферометр, представляющий собой две антенны, разнесенные на расстояние, называемое длиной базы. Система с такой архитектурой измеряет разности фаз прихода сигнала на антенные элементы А1 и А2 и расстояние до элемента А1.

Стандартное отклонение оценок угла прихода для такой системы уменьшается с увеличением длины базы. Однако в то же время при наличии только одной опорной радионавигационной точки (далее – ОРНТ) однозначное позиционирование возможно только при длине базы, не превышающей половину длины волны. Если же длина базы больше, то для каждой разности фаз существует несколько возможных точек, в которых может находиться пользователь. Этот факт называется проблемой фазовой неоднозначности, а ее решение, соответственно, разрешением фазовой неоднозначности. С другой стороны, увеличение длины базы уменьшает флуктуационную составляющую ошибки позиционирования пользователя.

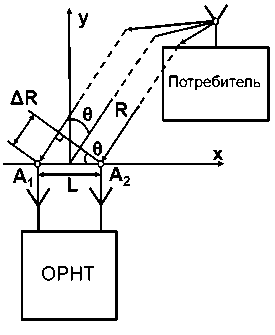
Рисунок 1. Схема измерений угломерно-дальномерной системы Источник: здесь и далее рисунки выполнены авторами.

Данная работа посвящена решению этой проблемы на основе комплексирования радио- и инерциальных измерений. Для получения однозначного решения в случае длины базы, большей половины длины волны, необходимо сформировать некоторый критерий, по которому из всего множества потенциальных решений будет выбрано одно.

Разрешение фазовой неоднозначности на основе инерциальных измерений ...

Постановка задачи

Необходимо сформулировать и экспериментально подтвердить критерий выбора максимально допустимой длины базы ОРНТ угломерно-дальномерной ЛНС с заданными точностными характеристиками, позволяющий однозначно определять координаты потребителя СШП ЛНС и инерциального измерительного блока (далее – ИИБ). Разрешение фазовой неоднозначности становится возможным за счет использования дополнительной информации – оценок угла курса, получаемых алгоритмом пешеходного счисления пути (далее – ПСП), обрабатывающим измерения ИИБ.

Угломерно-дальномерная (далее – УД) система позволяет измерять как дальность до потребителя R , используя временную задержку сигнала, так и угол прихода сигнала è , который можно определить как угол между нормалью к основанию антенной решетки и лучом на цель, используя разность фаз радиосигнала на каждой антенне. Эти значения могут быть пересчитаны из полярной в декартову систему координат с помощью функциональных зависимостей:

0 = asin

A R

L

x=

R-Ар-Л 2n L

y=R

\^A 1 \ [ 2nL J где L - длина базы ОРНТ; Л - длина волны излучаемого сигнала.

Радиоизмерения угла прихода СШП ЛНС наблюдаются на фоне аддитивного белого гауссового шума:

^

r = r pad + n pad =

R + ⁿ R

A ^ J [ n a?

где nR и nA^ - аддитивный белый гауссов шум наблюдений по дальности и разности фаз с нулевым ожиданием и дисперсиями oR и <тAv.

В результате экспериментов, проведенных в статичных условиях, было установлено, что среднеквадратическое отклонение (далее – СКО) составляет до 3 см и до 7 градусов. В результате работы алгоритмов ориентации СКО определения угла прихода сигнала составляет 2-3 градуса при систематической ошибке в градус. В данных экспериментах использовался комплект PDoA beta kit компании Decawave, в комплект которой входят ОРНТ DWM1002 и потребитель – носимый радиомодуль DWM1003, на борту которого расположен ИИБ. Особенностью данной системы является наличие на ОРНТ DWM1002 двух приемопередатчиков DW1000, тактированных от общего опорного генератора, что позволяет измерять не только задержки распространения сигналов между ОРНТ и носимым радиомодулем потребителя, но и разность фаз прихода сигнала на каждый из антенных элементов ОРНТ. Ввиду особенностей архитектуры обмена сообщениями между ОРНТ и носимым модулем дальность измеряется лишь до одного из элементов антенной решетки.

Зависимость измеренных разностей фаз от угла прихода сигнала, называемая пеленгационной характеристикой УД ЛНС, описывается следующей формулой:

Ap = mod | 2 п - sin( ^ )-— + п ,2 п |- п

\          Л )

Пусть пользователь находится в произвольной области внутри закрытого помещения.

Этой области соответствует определенный сектор на пеленгационной характеристике антенной решетки. На Рисунке 2 показаны все возможные траектории движения пользователя. На Рисунке 3 показана пеленгационная характеристика, соответствующая длине

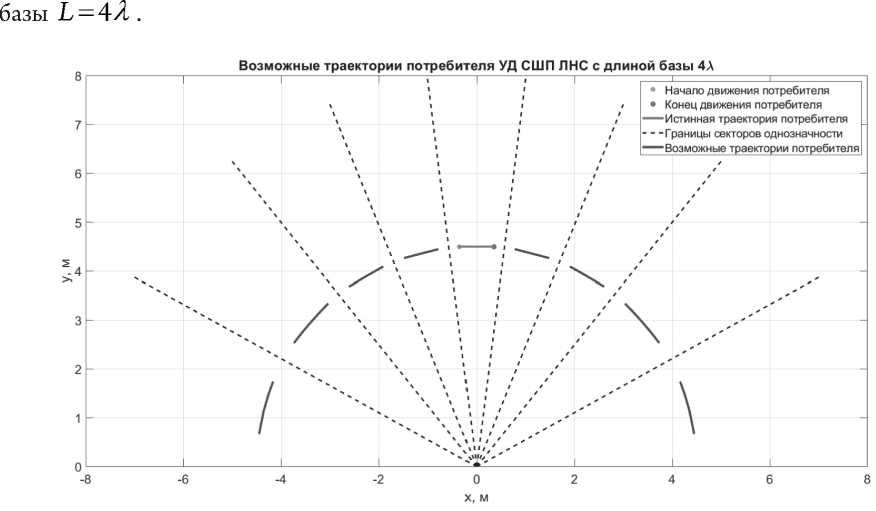
Рисунок 2. Все возможные положения потребителя

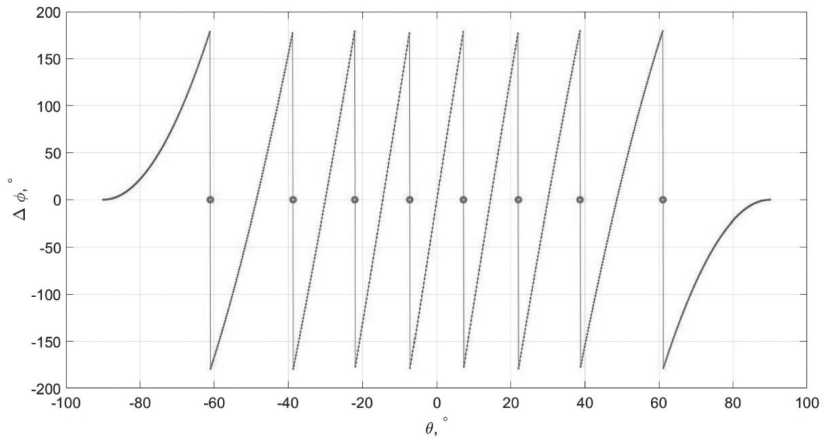
Рисунок 3. Пеленгационная характеристика, соответствующая длине базы L — 4 Л (точками обозначены границы секторов, показанных на Рисунке 2)

Количество секторов на пеленгационной характеристике определяется длиной базы ОРНТ, эта величина может быть определена по известной зависимости как

Разрешение фазовой неоднозначности на основе инерциальных измерений ...

K = 2 fix ^f L} +1

1 2 )

где fix - округление усечением.

Каждому из секторов однозначности присваивается целый порядковый номер. Полный набор номеров секторов M определяется в зависимости от общего количества сек- торов, как показано ниже.

M =

—

K — 1 K — 1 ...

Значение углового сектора однозначности зависит от соответствующего целого числа ^Ki :

kO i = asin\

Используя оценку курсового угла потребителя, алгоритм ориентации и его последующее сравнение с курсовыми углами во всех возможных секторах, полученных аппроксимацией по методу наименьших квадратов (далее – МНК), можно определить истинный сектор, в котором находится потребитель, иными словами, однозначно позиционировать потребителя. Для нахождения сектора, в котором находится потребитель, предлагается использовать следующий подход.

Угол пеленга определяется по оцененным координатам с известным СКО как

9 MHK = atan2

ˆˆ yMHK конец yMHK начало

ˆˆ

^X MHK конец ^X MHK начало

где ^конец^MHKK^ y M _H K^aчa.o ■ ^X MUKua4a.o ^- оЦенКИ координат начала и конЦа шага потребителя, соответственно.

Для аппроксимации МНК была выбрана линейная модель, в которой каждая из координат аппроксимируется во времени отдельно:

x MHK =k _x t+b _x

7 К J К                      У MHK kyt+by где kx, bx, ky, by - коэффициенты полиномов, оцененных с помощью МНК; t - набор моментов времени на интервале шага.

Найденные коэффициенты k _x и k _y можно выразить через координаты и соответствующие им моменты времени, оцененные с помощью МНК:

k . =

^k y =

л                  .                    A

; x v x де y MHK конец ^, MHK конец ^,y MHKначало ^, MHK начало

А

MHK конец лмнк мчало — iMHK конец MAKK начало

ˆˆ yMHK конец ~yMHKначало —

MHK конец MAKK начало

– оценки координат конца и начала шага потребите-

ля, полученные с помощью МНК.

Используя зависимости (7) и (9), оценку угла курса потребителя на интервале временного шага по данным радиоизмерений можно представить как

^

⁹ MHK

Для определения истинного сектора однозначности, в котором находится траектория потребителя, абсолютные значения найденного вектора невязок / _мнк -I//_псп должны быть аппроксимированы по числу секторов однозначности М ^ полиномом второго порядка (см. Рисунок 4).

Таким образом, критерий завязки записывается следующим образом:

M = round [ mm ( f _MH K ( м , )) ] (11)

где f _MHK ( M_t ) - зависимость модуля невязок между оценками угла курса траектории движения потребителя в каждом из возможных секторов однозначности по радиоизмерениям и оценкой угла курса по алгоритму ИИБ, полученная с помощью МНК.

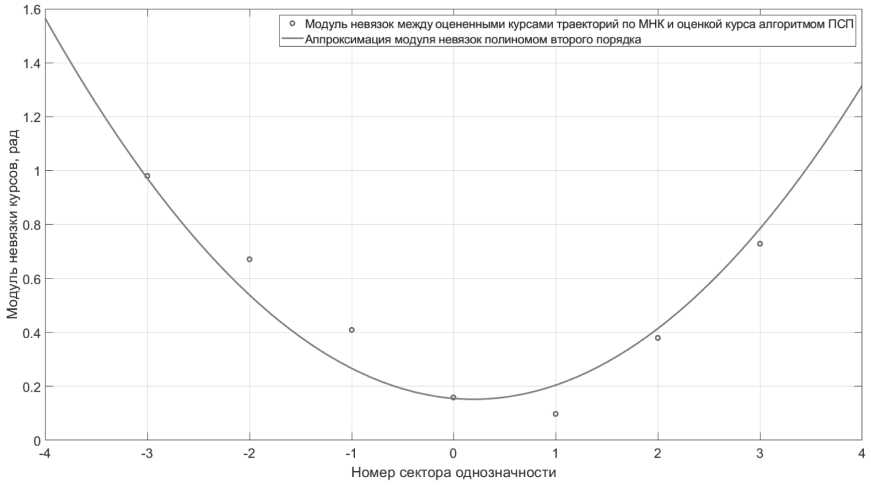
Рисунок 4. К объяснению критерия завязки траектории

Вывод выражения

Как уже говорилось выше, оценив угол курса потребителя и сравнив его с углами курса во всех секторах, можно однозначно определить местоположение цели, однако на практике радио- и инерциальные измерения наблюдаются на фоне белого гауссова шума. Авторы предлагают критерий для однозначного определения координат потребителя для определенной длины базы ОРНТ. Этот критерий состоит из двух условий. Первое условие заключается в необходимости того, чтобы границы соседних секторов, в которых курс может быть оценен в результате аппроксимации, не пересекались.

Измеренная разность фаз между принимаемыми сигналами зависит от углов прихода и амплитуд интерферирующих волн. Погрешность измерений разности фаз характеризуется следующими факторами:

• •    несовершенство среды распространения радиоволн [10–12];

• •    внутренние шумы оборудования и внешние помехи [13];

• •    неидентичные тракты приема и усиления от антенн до фазометров и, следовательно, наличие неучтенных фазовых сдвигов.

Разрешение фазовой неоднозначности на основе инерциальных измерений ...

Совокупность этих факторов приводит к случайной ошибке в измерении разности фаз Аф . Если известна о _д ^ , тогда, зная функциональную зависимость [14], можно получить выражение для расчета СКО определения угла пеленга:

^o а^^л g =

2 n L ■ cos( 0 )

СКО определения k _x и k _y :

°кХ

N 2 .£ ( xi ^- k x ti ^- b x )

N 2

I ( N - 2 ) =1 ( ti - 1 )

g

ky

N 2

^=1 yi “ ^k y ti “ ^Ь У )

N 2 ( N - 2 ) =1 ( ti-1 )

где N – количество измерений за время одного шага.

В свою очередь, мы можем оценить ошибку в определении угла курса о\^ , которая определяется в результате аппроксимации МНК, используя ok и ok . Поскольку значение Фмнк вычисляется из измеренных значений нескольких независимых физических ве- личин на основе известного закона(7) Ф„ f(k,k ), то, чтобы найти ошибку о , мнк      x у)                               ^мнк воспользуемся известным из математического анализа свойством: малые приращения гладких функций многих переменных складываются линейно, то есть действует принцип суперпозиции малых приращений. Тогда, используя формулу для нахождения дисперсии суммы независимых физических величин [15], получим соотношение

^LSM

I 02 + kx

^дф мнк S k

² k y

ду ^ мнк_ = k y

S k x     k 2 + k y ,

^дфмнк ₌_ К

Skу ■ k2+ky

Таким образом, первое условие можно представить в виде (см. Рисунок 5) а а со    . + со   . <----

Р мнк i      У мнк i ^{+ 1}      3

где m^ , m^ + 1 - математическое ожидание углов курса соседних секторов.

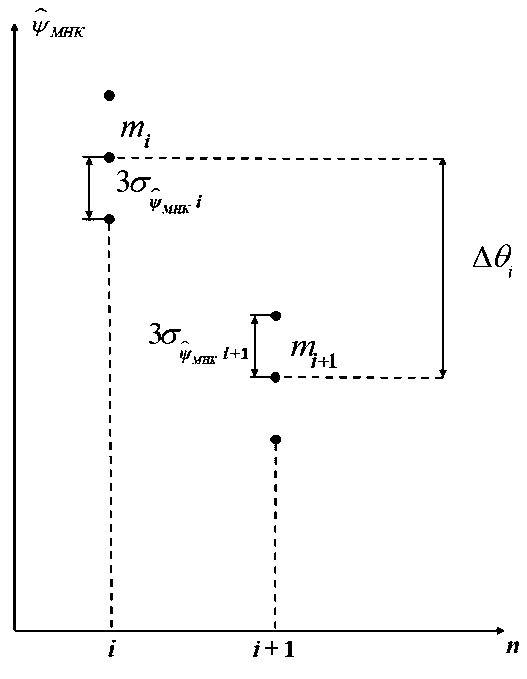
Рисунок 5. Рисунок, поясняющий первое условие

В дополнение к тому, что было рассмотрено выше, необходимо, чтобы разброс оценок угла курса алгоритма ориентации по измерениям инерциального блока не превышал разброса оценок курса по МНК одного сектора и находился в его пределах, что является вторым условием критерия (17) (см. Рисунок 6). Таким образом, первое условие (16) дополняет второе условие, обеспечивая достоверное определение сектора однозначности, в котором находится потребитель:

m — i

—

<

3 a-  . , >  m-  + 3 a

V mhk ^{1 1}     ^ ПСП       ^V псп

mM

+ 3 a <  m  — 3 a

V mhk ¹⁺¹     V ПСП        W ПСП

где a

У ПСП

– СКО оценки угла курса по алгоритму ориентации; m

^V ПСП

оценка угла кур-

са, &а _П с _П - систематическая ошибка определения угла курса по алгоритму ориентации.

Разрешение фазовой неоднозначности на основе инерциальных измерений ...

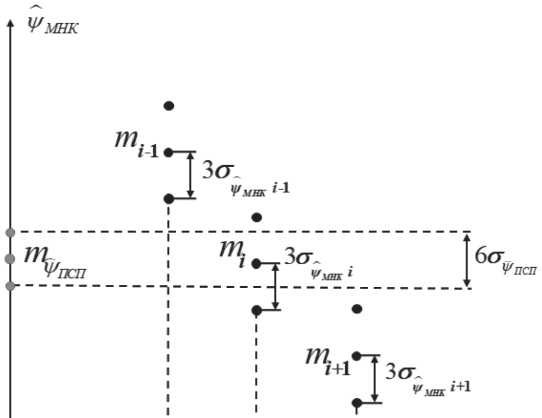
Рисунок 6. Рисунок, поясняющий второе условие

Моделирование

Эксперименты, подтверждающие выведенные соотношения (16) (17), состояли из 1000 реализаций и заключались в следующем. Потребитель находился в нулевом секторе пеленгационной характеристики, угол курса равен

0 ° ±3 ^   + A CT ( CT

V псп       ^псп V псп

= 2.65°, ACT псп

= - 1 ° ) . Выбор этого сектора обусловлен

наимень-

шим размером углового сектора однозначности, из этого следует, что если в этом секторе можно однозначно определить координаты потребителя, то это можно сделать и во всех других секторах. Истинный угол курса был выбран таким, чтобы привести к наибольшей ошибке в оценке угла курса в результате аппроксимации МНК. Угломерно-дальномерные

измерения антенн СШП ЛНС проводятся с известными дисперсиями ctR=9 см и стАр = 49°. Требуется однозначно позиционировать потребителя или, другими словами, определить истинный сектор, в котором он находился. На практике потребитель в начале траектории находится в пределах 4 м от ОРНТ СШП ЛНС, поэтому имеет смысл рассмотреть предельную ситуацию. В первом эксперименте (см. Рисунок 7) длина базы ОРНТ была выбрана, используя условия (16) (17), координаты пользователя в прямоугольной системе координат x=0,y=4 .

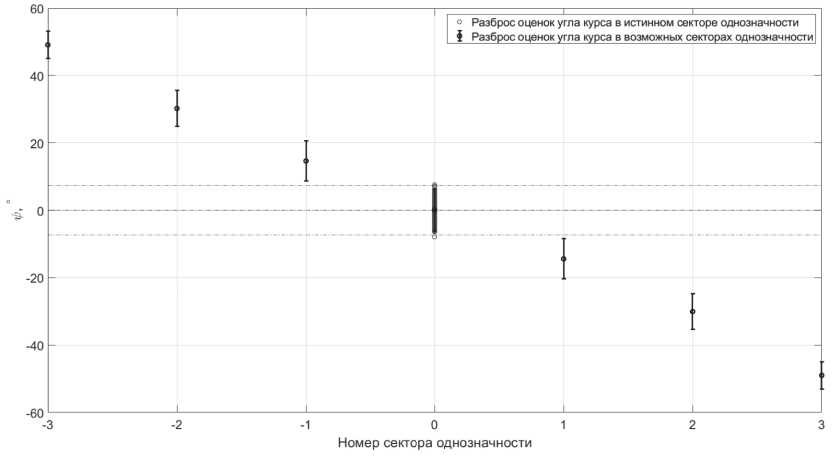
Рисунок 7. Границы всех секторов при L = 4 Л и ^ псп = 0 °

Как видно, условия (16) (17) не нарушаются, значит, траектория может быть завязана. По результатам первой серии экспериментов алгоритм неверно определил сектор, в котором находился пользователь, – менее чем в 1 % случаев при использовании условия (16) (17). Для второй серии экспериментов (см. Рисунки 8 и 9) была выбрана длина базы

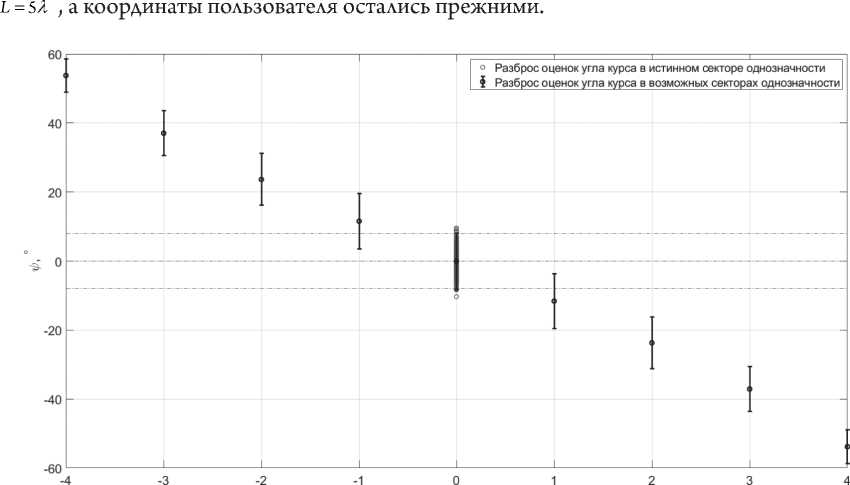
Номер сектора однозначности

Рисунок 8. Границы всех секторов при L = 5 Л и ^ псп = 0 °

Разрешение фазовой неоднозначности на основе инерциальных измерений ...

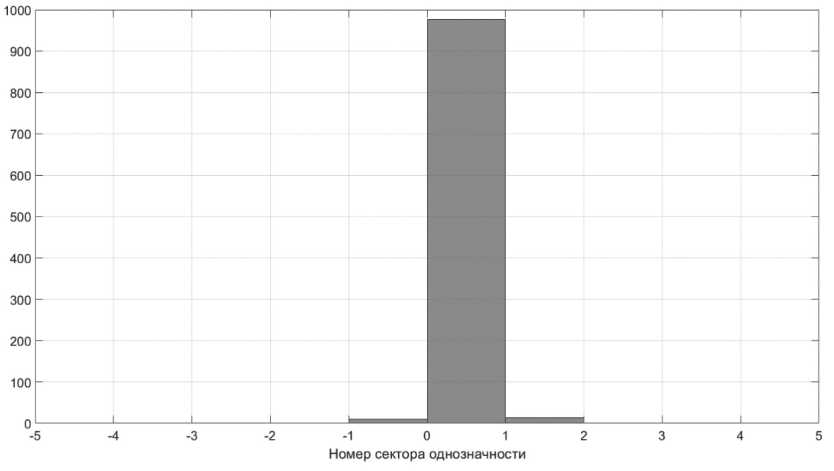
Рисунок 9. Гистограмма секторов расположения пользователя, выбранных по критерию о при L = 5 Л и ^ ПСП = 0

Результаты показывают, что условия (16), (17) не выполняются, что привело к увеличению вероятности ложного определения истинного сектора однозначности, и она составила 5 %.

Чтобы продемонстрировать рост процента ложного определения истинного сектора однозначности с увеличением длины базы, был повторен эксперимент с L = 6Л (Рисунки

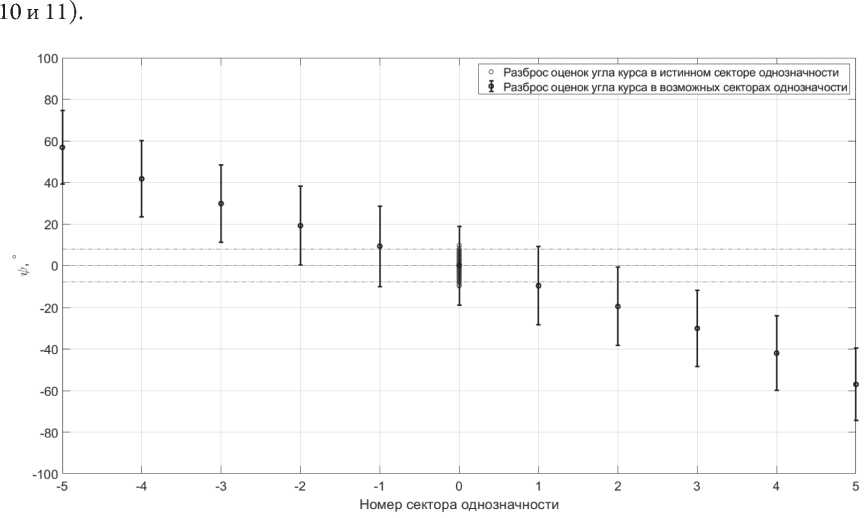
Рисунок 10. Границы всех секторов при L = 6 Л и ^ псп = 0 °

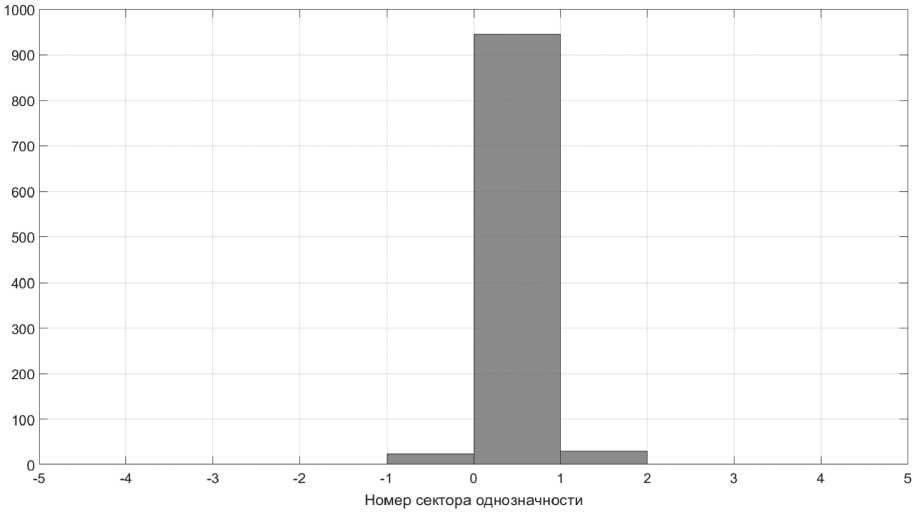
Рисунок 11. Гистограмма секторов расположения пользователя, выбранных по критерию при L = 6 Л И У псп = 0

При длине базы L = 6Л алгоритм неверно определил истинный сектор, в котором находился потребитель, – в 11 % случаев.

Рассмотрим         другую          ситуацию,          в         которой

+Да псп

(а~ у псп

Упс и =90 ° ±3 ^ г“ ^с “         ^у псп — тс

динатах потребителя (см. Рисунок 12).

= 1.5°, Да псп

= -1°) при неизменных начальных коор-

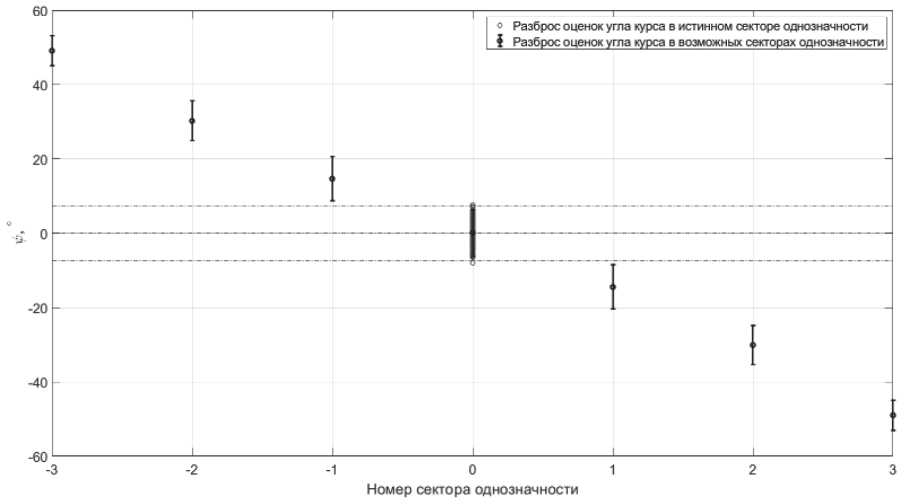
Разрешение фазовой неоднозначности на основе инерциальных измерений ...

Как видно, в данной ситуации условия (12) и (13) выполняются, благодаря чему алгоритм верно позиционировал пользователя во всех случаях. В результате анализа ряда проведенных имитационных экспериментов можно сделать вывод, что для однозначного позиционирования потребителя данной ЛНС и ИИБ необходимо выполнение сформированного критерия. Этот критерий, как уже было сказано выше, состоит из двух условий; в случае, когда эти условия не выполняются, становится невозможным достоверно определить координаты потребителя.

Заключение

Предложенный критерий подтвердил свою работоспособность в эксперименте. Максимально допустимая длина основания антенной решетки при заданных точностных характеристиках, а именно & _псп = 2,65 ° , & R2 = 9 cm и '' 2 ^ = 49 ° , составила L = 4 Л . В случае, когда используются другие системы и датчики с заданными характеристиками, предложенный критерий позволяет оценить максимальную длину базы.

В качестве следующих этапов работы в этом направлении планируется использовать измерения барометра для получения дополнительной информации о высоте расположения потребителя над плоскостью, в которой расположена опорная радионавигационная точка.