Разрушение частиц ферромагнитного материала в магнитовибрирующем слое с высокой порозностью

Введение. Порошковая металлургия среди разнообразных способов передела металлов позволяет создавать принципиально новые материалы. Кроме того, методами порошковой металлургии можно получать уникальные свойства, которые другими методами получить практически невозможно.

При размоле металлических порошков можно комбинировать различные виды воздействия: сжатие, удар, истирание. Причем, первые два вида имеют место при крупном помоле, второй и третий – при тонком измельчении. Особое место в ряду размольных устройств, обеспечивающих сухой помол, занимает бильная мельница, в которой ферромагнитный материал переводится в состояние псевдоожижения. Описанная в работе [1] конструкция мельницы позволяет управлять гранулометрическим составом порошковой среды, изменяя индукцию и градиент индукции магнитного поля. Однако наличие вращающихся бил в конструкции мельницы повышает энергозатраты и износ механизмов.

Целью работы является получение соотношения между механическими характеристиками материала частиц и параметрами электромагнитного поля, при которых происходит разрушение частиц в магнитовибрирующем слое высокой порозности за счет соударений со стенками рабочего объема устройства.

Теоретическая модель. При решении поставленной задачи были сделаны следующие допущения:

– энергия, сообщаемая частицам дискретной среды внешним переменным полем с индукцией B = B + B cos гоt, расходуется без потерь на разрушение частиц (B^ - постоянная состав- c V                                                               c ляющая индукции магнитного поля, BV - переменная составляющая индукции магнитного поля, го - частота переменного поля), т.е. диссипацией энергии за счет взаимодействия с непрерывной фазой при движении частиц пренебрегаем;

• –    частицы дисперсной среды представляют собой сферы с вмерзшими магнитными моментами;

• –    постоянная и переменная составляющие индукции магнитного поля взаимно перпендикулярны;

• –    подкачка энергии от поля осуществляется через поступательные степени свободы частиц;

• -    Bc <_V , так как в противном случае дисперсная система переходит в структурированное состояние.

С учетом принятых допущений уравнение энергии, передаваемой внешним полем частице в единицу времени при поступательно-колебательном движении, записывается в виде [2]:

E   = _± ( P S B ylS y ) ²

п-к 2n mto где P - магнитный момент частицы; dBNpy — градиент поля; m - масса частицы.

Предполагая, что порозность частиц в магнитовибрирующем слое высока, можно считать, что соударения между частицами отсутствуют. При этом следует ожидать разрушения частиц только при соударении со стенками объема, в который они помещены. Кроме того, будем считать, что размеры рабочего объема и частота поля таковы, что время пролета частиц от одной стенки к другой соответствует ^T ₂ [2].

При измельчении путем раздавливания, раскалывания, удара затраты энергии Е_р на разрушение сферической частицы при степени измельчения Z_u соответствуют гипотезе В.Л. Кирпи-чёва [3], согласно которой:

E ^-"пе ( Z - - 1 ) '                              (2)

где a - предел прочности при разрушении материала; d k - конечный диаметр частицы;

ZU = —                           , dк – степень измельчения материала; dн – начальный диаметр частицы; Е – модуль

Юнга материала.

Разрушение частиц будет наблюдаться при условии, что

T

Ep = ^ЕП - К " 2 .

С учетом (1) и (2) можно записать:

na ² dK /Z 3 - 1 L P ² f d B _v f _ T

12 E ( и ) 2nmto( dy J 2 .(3)

Выражение (3) можно представить в виде:

a2d3p3 yJ2 d3 f5^f a dK (ZU 1) н I dy J 1?       =         2       .

E pto

_ Jn d_H _pn

При этом принимаем P =  6  , где J - намагниченность материала частицы; m = 6

T _п где p - плотность материала частицы, 2 = to "

После несложных преобразований (4) приобретет вид:

ZU =

1 - EJ² f 6 B y) ² pto ² a ² I ^{d y} J

.

Здесь

EJ ²

.

2 2 = p to a

д B _v Тл д у ’ м

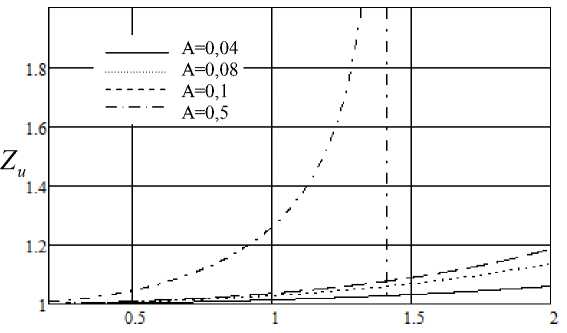
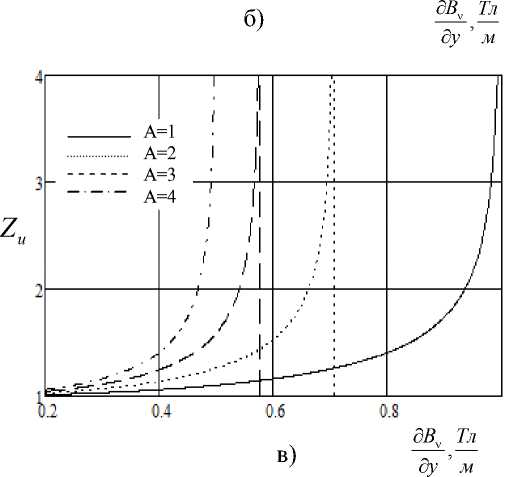
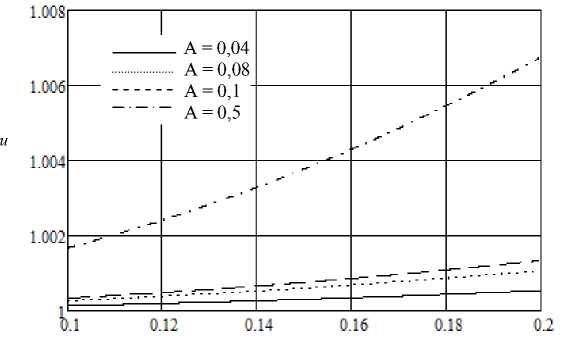
Зависимость степени измельчения частиц от градиента индукции магнитного поля частотой 50 Гц;

изменение градиента индукции магнитного поля и коэффициента А: а - ^д B v _ 01 ^ о зТл/ а _ 0 04 ^ 05 A 2 ^c4 м 2 ;

а у      ’ ' ’ /м,          ,    ' , кг²

б ^- ^ = 0,5 ^ 2W, А = 0,04 ^ 0,5 A ²^ ^; в ^- ^ B v = 0,2 ^ 1Ту , а = 1 ^ 4 ^А2^с4м2

д у     ’       /м,         ,      , кг²            д у     ,       ^/м,                кг²

Коэффициент А зависит только от механических и магнитных характеристик материала частиц, а также от частоты переменного поля. С учетом принятых обозначений (5) можно записать:

Z

и

1- A (^ f

( 5 y )

Из полученного соотношения очевидно, что с ростом градиента индукции поля степень измельчения материала растет.

Предполагаем, что коэффициент А для различных магнитных материалов существенно меняется при фиксированной частоте за счет изменения механических и магнитных характери- A ² c ⁴ м ²

стик от единиц   c 2м до сотых долей. На рисунке представлен расчет для различных А. Анализ кг2

кривых позволяет сделать вывод, что для сильномагнитных материалов, либо для материалов, имеющих невысокий предел прочности при разрушении, измельчение частиц при единичном акте соударения начинается в полях с градиентом индукции порядка десятых долей Тл/м (рисунок, б ). Например, для феррита бария: намагниченность J = 320 • 103 АМ , модуль Юнга

E = 1,9 • 10 Н/ 2 , плотность р = 5Л10 ^3ю/, , прочность на разрушение о=310⁷Н/₇ [4], коэффици- м                       м³                                    м²

ент А = 0,04. При этом уменьшение диаметра частиц в 1,1 раза происходит в полях с градиентом индукции 0,4 Тл/м, а в 1,5 раза – 1,25 Тл/м.

Следует отметить, что для каждого материала существует значение градиента индукции, при котором происходит интенсивное разрушение частиц.

Например, для А = 1

А ² с ⁴ м ²

эффективное разрушение частиц наступает при градиенте кг ²

индукции более ⁰,6 ^ 0,7 ТлМ , а

А ² с ⁴ м ²

при А = 2         такой же процесс реализуется в полях с гра- кг2

диентом индукции 0,4: 0,5 ТлМ .

Кроме того, при малых градиентах индукции от частицы отделяется малая часть, что происходит и при больших градиентах индукции. Это следует учитывать при выборе параметров поля. Выводы. Определена возможность размола порошков магнитных материалов в неоднородном магнитном поле за счет соударения частиц со стенками рабочего объема. Проведен расчет градиента индукции магнитного поля, при котором происходит процесс разрушения частиц порошка даже при единичном акте взаимодействия со стенками рабочего объема. Это позволяет предположить возможность создания конструкции размольного устройства, не имеющего механически движущихся частей.