Разрушение межагрегатных связей между частицами почвы в процессе водной эрозии

Сопротивление частиц почвы отрыву потоком воды, как правило, намного больше тех сил гидравлического происхожде- ния, которые испытывает ложе потока в целом, а также и слагающие его частицы грунта. Именно поэтому Ц.Е. Мирцхулава в предложенном им еще в 1970 г. уравнении эрозии использовал представление об усталостном разрушении связей между почвенными частицами, а также и частицами грунта под воздействием динамических нагрузок, испытываемых ложем потока вследствие местных пульсаций скорости движения воды. Исследования по усталостной прочности грунтов и скорости их размыва показали сходство этих процессов, поэтому по аналогии с уравнением, опи- сывающим кривую усталостной прочности, число циклов напря- жения (N) до момента отрыва частицы можно представить в виде:

N =

v ∆ ² _x

2 v ∆ доп

-

где vΔx и vΔдоп соответственно придонная скорость на высоте выступов шероховатости на расстоянии х от начала ручейка и допустимая (неразмывающая) скорость. Соотношение квадратов этих скоростей эквивалентно соответственно напряжению разрыва в начальный момент воздействия нагрузки на частицу почвы и в момент ее отрыва потоком воды. Из уравнения (1), зная частоту пульсаций скорости в потоке, нетрудно определить число частиц срываемых потоком в единицу времени и, распространив это чис- ло на единицу площади, получить уравнение смыва в виде:

⁽ i доп

q = 0.0000064 ytod?

где q – смыв почвы с единицы площади; d – диаметр отрываемых частиц; γ – плотность частицы; ω – частота пульсаций скорости в потоке. Позже Ц.Е. Мирцхулава (1970) частоту пульсаций в склоновых потоках принял как константу. Допустимая скорость, согласно его представлениям, является функцией корня квадратного из веса частицы почвы в воде и усталостной прочности почвы на разрыв (Су). Последняя определяется по зависимости:

C y = 0.035 C ,                         (3)

где С – сцепление, определяемое вдавливанием сферического штампа в почву.

М.А. Неаринг с соавторами (Nearing et al., 1991) уделяли много внимания этому вопросу. Исследования сопротивления разрыву 33 различных почв США показали, что по этой характеристике все почвы укладываются в диапазон от 0.9 до 3.2 кПа. Анализ результатов его исследований на моноагрегатных образцах почв показал, что их сопротивление разрыву укладывается в приведенный диапазон и на три порядка больше, чем касательные напряжения на дне склоновых мелководных потоков. Тем не менее, образцы почв успешно размывались. Для объяснения этого парадокса М.А. Неаринг (Nearing, 1991) использовал результаты исследований Грасса (Grass, 1970), согласно которым касательные напряжения в точках придонной области, где происходит отрыв вихревых возмущений (burst event), на два порядка превосходят среднюю величину касательных напряжений на дне потока, полагая, что именно в этих точках происходит отрыв частиц почвы. Поскольку отрыв вихрей со дна потока носит стохастический характер, то и уравнение отрыва частиц почвы включает вероятностный блок. Однако такое решение представляется не вполне корректным, так как касательное напряжение в точке отрыва вихря, хотя и на два порядка выше, чем среднее значение касательного напряжения, и все же оно на порядок ниже сопротивления образца почвы разрыву.

Вместе с тем решение этой проблемы, предложенное Ц.Е. Мирцхулавой, также нельзя признать безупречным. Если принять, что сцепление почвы, определяемое методом вдавливания сферического штампа в грунт при полном насыщении водой (Цитович, 1963), эквивалентно сопротивлению породы на разрыв, как это полагает Ц.Е. Мирцхулава (1966), то усталостная прочность на разрыв, того же порядка, что и касательное напряжение в местах отрыва вихрей. Таким образом, решение проблемы отрыва частиц связного грунта склоновыми водными потоками с позиции усталостного разрушения связи между частицами грунта представляется не вполне корректным.

Имеются и другие факты, противоречащие представлению о гидравлической природе сил, ответственных за разрушение связей между частицами почвы. Согласно многим моделям эрозии (Foster, 1982; Rose, 1985 и др.) интенсивность смыва находится в линейной зависимости от величины активного фактора эрозии. В гидрофизической модели эрозии (Ларионов, Краснов, 2000) интенсивность смыва пропорциональна кубу скорости потока в области скоростей превышающих пороговые значения в 1.5–2 раза. Для подтверждения этого положения проведены опыты по размыву модельных образцов почвы плотностью 1.2 г/см3 в широком диапазоне скоростей. Эксперименты дали положительные результаты (рис. 1), кроме области малых скоростей была получена линейная зависимость между смывом и кубом скорости потока.

Однако при исследовании образцов более высокой плотности обнаружено, что зависимость между скоростью размыва образцов и кубом скорости потока имеет отчетливый перелом (рис. 2).

Оказалось, что интенсивность отрыва частиц почвы не пропорциональна кубу средней скорости потока во всем исследованном диапазоне скоростей. Начиная с некоторой скорости, наблюдается резкое выполаживание линии тренда на графике зависимости интенсивности смыва от куба скорости потока.

Первая попытка объяснить это явление основывалась на усталостном подходе к нарушению связей между частицами почвы. Как известно, в процессе усталостного нарушения циклические противоположно направленные нагрузки приводят к движению относительно друг друга материала в точках с дефектом структуры, где со временем возникают трещины, а потом и разрушение материала. В случае однонаправленных циклических нагрузок, что характерно для частиц, выстилающих ложе потока, возвратно поступательное движение в материале может иметь место лишь при наличии в материале упругих свойств. Если допустить, что почвенные частицы обладают свойством упругости, то можно принять, что отрыв частиц потоком воды происходит вследствие многократных циклов возвратно поступательных движений, которые возможны лишь в том случае, когда минимальные значения нагрузок гидравлической природы будут меньше сил упругости частицы. С ростом минимальных нагрузок амплитуда возвратно поступательных движений будет уменьшаться, что может служить причиной относительного замедления интенсивности отрыва частиц с увеличением скорости потока. При неограниченном росте скорости потока минимальные пульсационные нагрузки, очевидно, превысят силы упругости почвенных частиц, вследствие чего возвратно поступательные колебания частиц пре-

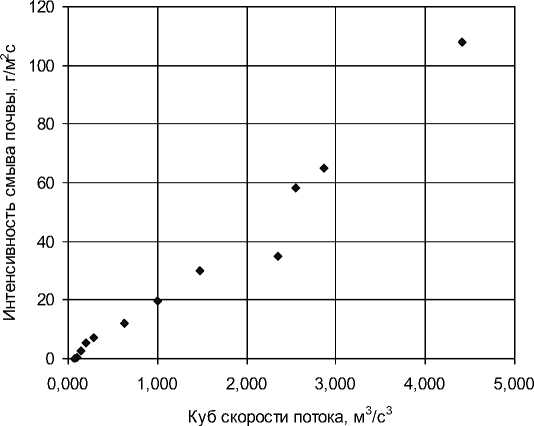
Рис. 1. Зависимость интенсивности размыва модельного образца почвы плот ос ю 1 2 /с ³ о ба с о ос о о а

18,0 16,0 14,0 05 -D 12,0 s 10,0 5  8,0 ш 6,0 1  4,0 2,0 л n -
		♦
	♦ ♦
0,0 0	0      1,0      2,0      3,0      4,0      5,0      6						0

Куб скорости потока, м3/с3

Рис.                                                         очвы плотностью 1.5 г/см3 от куба скорости потока.

кратятся, и соответственно прекратится их отрыв. Однако размыв модельных образцов почвы не прекращался и при скорости более 7 м/с. Таким образом, идея усталостного нарушения связей между почвенными частицами в процессе размыва и в этом случае не работает.

Случай подсказал, в каком направлении следует искать решение проблемы нарушения связей между частицами в процессе эрозии склоновыми потоками, касательные напряжения, на дне которых на три порядка меньше, чем сопротивление почвы разрыву. Однажды при проведении серии экспериментов при постоянной скорости потока температура воды увеличивалась в результате работы насоса с 13 до 25ºС, при этом скорость размыва образцов почвы увеличивалась. В связи с этим был проведен эксперимент для изучения влияния температуры вода на скорость размыва образцов в диапазоне от 0 до 25ºС с шагом 5ºС (рис. 3).

Оказалось, что при увеличении температуры воды на 10ºС скорость размыва (эродируемость) увеличивается в 1.5–1.6 раза, что практически укладывается в рамки правила Вант-Гоффа, которое отражает влияние скорости движения молекул, реагирую-

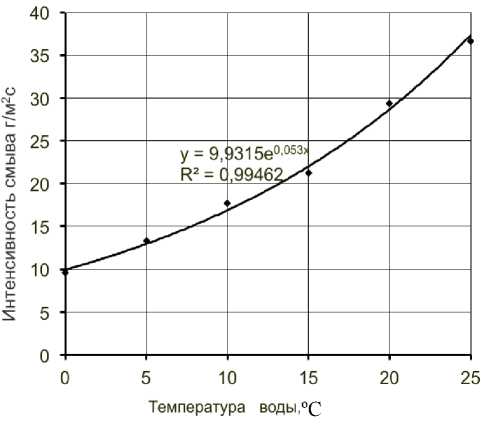
Рис. 3. Влияние температуры воды на скорость размыва образца почвы.

щих веществ, частоты и силы их соударений, на скорость реакции. Из этого следует, что разрушение связей между частицами почвы – это результат действия не гидравлических сил, а кинетической энергии молекул воды.

В связи с этим проведены поисковые исследования, целью которых являлись: 1) разработка методики определения скорости разрушения связей между частицами почвы; 2) поиск факторов, определяющих скорость разрушения межагрегатных связей в модельных почвенных образцах.

Разрушение связей между частицами почвы визуально не определяется, механически отделить частицы, лишившиеся связи с почвенной массой, также невозможно. Наиболее оптимальным представляется использование потока воды для удаления частиц, лишившихся связи с нижележащими частицами, с поверхности образца. В связи с этим для оценки роли воды как вещества, вызывающего нарушении связей между частицами почвы, была принята следующая методика. Вода подавалась в лоток с паузами, в продолжении которых поток воды отсутствовал, но почвенный образец находился под водой слоем 1 см. Эксперимент начинался с паузы. На 1–2 см ниже образца помещали глухую перемычку высотой несколько более 1 см и наливали воду, в количестве, обеспечивающем глубину воды в 1 см. После паузы следовала активная фаза эксперимента – перемычка снималась, и включался насос. Вода подавалось в лоток заданное время. Затем насос отключался, вновь устанавливалась перемычка, а образовавшаяся емкость заполнялась водой. За первые же секунды смывались с поверхности образца все потерявшие связь с образцом частицы. Визуально можно наблюдать этот процесс – по лотку движется масса частиц почвы (рис. 4), в то время как при традиционной методике испытания образцов обычно изредка наблюдаются отдельные частицы или группы частиц. С увеличением продолжительности пауз количество частиц, лишившихся связи, увеличивается с некоторым замедлением (рис. 5). Это может быть объяснено двумя моментами. По мере накопления частиц лишенных связей они все сильнее придавливают (пригнетают) нижележащие частицы, что затрудняет или вовсе прекращает распространение процесса разрушения связей вглубь образца (вещества). Другое объяснение может заключаться в том, что молекулярное движение воды между почвенными частицами замедляется по мере опускания фронта

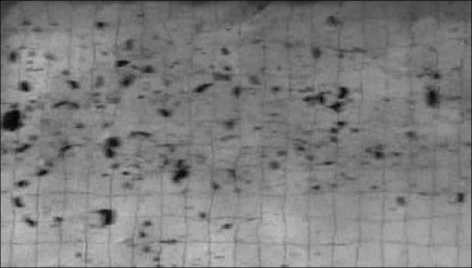
Рис. 4. Вид на лоток ниже образца. Темные пятна – частицы и группы частиц почвы, сорванные потоком.

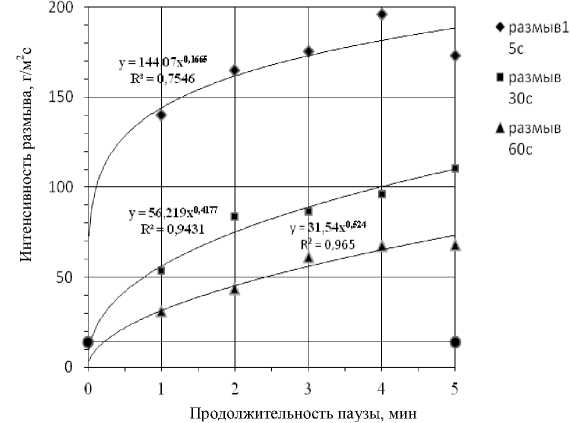
Рис. 5. Замедление интенсивности размыва образца с увеличением длительности паузы.

разрушения связей между частицами вглубь, что и приводит к снижению темпов нарушения связей между частицами.

Максимальные значения смыва уменьшаются с увеличением продолжительности паузы, что также свидетельствует о замедле- нии темпов разрушения связей по мере заглубления активного фронта.

Такой характер смыва, по нашему мнению, можно объяснить только тем, что ведущую роль в нарушении связей между частицами играют силы негидравлического генезиса, а именно силы межмолекулярного взаимодействия. Принимая во внимание это обстоятельство, резкий перелом на графике зависимости интенсивности смыва от куба скорости (рис. 2) можно объяснить следующим образом. На первом крутом отрезке линии графика скорость разрушения связей между частицами, происходящая под действием дипольных молекул воды, протекает быстрее, чем захват потоком воды свободно лежащих на поверхности образца частиц почвы. По мере увеличения скорости потока интенсивность захвата частиц растет, а вместе с этим ускоряется экспонирование воздействию воды как химического вещества слоев образца почвы с еще ненарушенными связями между частицами почвы. Иначе говоря, с ускорением захвата свободных частиц, увеличивается скорость разрушения связей еще между консолидированными частицами. Но когда способность потока захватывать неконсолидированные частицы, превысить скорость деконсолидации частиц водой, линия графика на (рис. 2) резко выполажи-вается. При дальнейшем увеличении скорости потока гидравлические силы начинают принимать участие в нарушении связей между частицами почвы в поверхностном слое образа почвы, и, вероятно, вклад гидравлических сил при дальнейшем увеличении скорости будет возрастать. Проверить и дать количественную оценку этому явлению можно только экспериментальным путем.

Из вышеприведенных фактов следует, что, вероятно, гидростатическое давление оказывает влияние на скорость разрушения связей между частицами под воздействием воды. Это может иметь место, если допустить, что гидростатическое давление не распространяется вглубь почвенного образца. Эта гипотеза была подтверждена экспериментально в четырех опытах по размыву образцов в гидравлической трубе, в которой гидростатическое давление поддерживалось в одном случае около 0, а в другом – около 1 атм. Во втором случае скорость размыва образцов почвы, и, следовательно, скорость разрушения связей между частицами почвы во- дой как химическим веществом была на порядок ниже, чем в первом случае (при нулевом гидростатическом давлении).

Наконец можно предположить, что сцепление между частицами почвы обеспечивается не только силами Ван-Дер-Ваальса, но и, например, полимерными соединениями. Для подтверждения этой гипотезы несколько образцов высушили, затем увлажнили до исходного состояния и после этого подвергли испытанию на размыв. И это предположение оправдалось. После высушивания образцы практически не размывались. Поскольку в естественных условиях почва все же смывается, предположили, что связи между частицами могут разрушаться и под воздействием циклического намокания и высушивания, а также и других факторах выветривания.

Таким образом, результаты исследований позволили выявить механизм разрушения связей между почвенными частицами в процессе водной эрозии, что послужит основой для разработки физически обоснованных моделей эрозии.

DESTRUCTION OF BONDS BETWEEN SOIL