Развитие метода синтеза геометрии канатов линейного касания

Стальной канат широко применяется в современной подъемно-транспортной технике, являясь при этом сложным и ответственным элементом. Одним из значимых факторов, обеспечивающих высокий технический ресурс и работоспособность, является линейный контакт проволок в прядях каната. Для расчета геометрии канатов линейного касания в работе [1], была получена система синтезирующих уравнений:

^ 2

^ 1 + ^ 2 ) ²

^Ф 12    x 12

2 .    2

1 + Г

= ^ 12

,        (1)

- 2 • r1 • r2 • cos(s12);

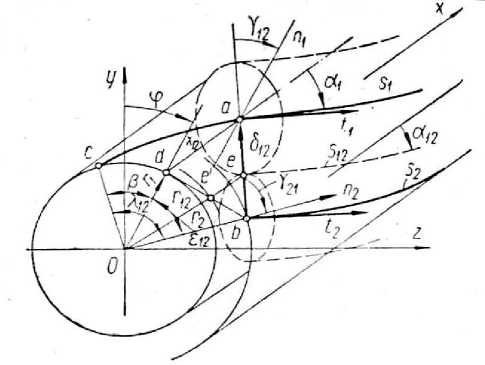
Рис. 1. Линейный контакт проволок в пряди каната

;

X12 = Г • tg(«2 ) • sin(^12 ) = Г • tg(«1 ) • sin£12 ) • ;

r

(3) h

112  2

2 •n; (4) £2 = ^2 — sin (^12 )• tg («1 )• tg («2 ) ,    (5)

Трансцендентное уравнение (5) имеет вспомогательный характер и может быть решено методом последовательных приближений. В качестве приближенного решения уравнения (5) было предложено использовать выражение (6):

где δ 12 – расстояние между точками a и b (см. рис. 1), δ 1 , δ 2 – диаметры проволок в пряди, х 12 – проекция отрезка δ 12 на ось x, r 1 , r 2 – радиусы винтовых линий проволок в пряди, α 1 , α 2 – углы свивки проволок, ε 12 – разность полярных углов точек a и b, λ 12 – полярный угол контакта.

ctg ( £ 12 ) =

tg(«1 )• tg («2) + cos( A2 ) sin (Я12)

Данное приближенное решение основывалось на малости угла β (см. рис.1) и, как следствие, приближенном равенстве β≈sin(β). При этом выражение (6) дает удовлетворительное решение уравнения (5). Однако возможны случаи, когда величина угла β будет значительна (например, при малом шаге свивки проколок в пряди каната). Кроме того, точность формулы (6) зависит от полярного угла контакта λ12, который в свою очередь связан с количеством проволок в слое пряди каната. Проведенные расчеты показали, что абсолютная погрешность выражения (6) может быть более одного градуса, а в некоторых случаях доходить и до 3-4 градусов. Следует отметить, что в работе [2] рассмотрено применение метода итерации для решения системы уравнений (1-5).

Учитывая вышесказанное, авторами предпринята попытка уточнить решение трансцендентного уравнения (5) для применения его в практических расчетах. Для этого запишем расстояние между точкой b винтовой линии 2-ой проволоки и винтовой линией 1-ой проволоки в зависимости от угла β, используя известную зависимость из аналитической геометрии в пространстве [3], и после преобразований получим:

^12 (Р) = V(Г1 " P^ • ctg2 (a2 )) + r12 + Г2 - 2 • rl • Г2 • cos(^2 - P)

Принимая во внимание, что β = λ 12 – ε 12 , перепишем уравнение (7) в следующем виде:

^ 12 ( ^£ 12 )    (j r r l ' ( A 2    ^£ 12 ) • c^{tg (a} i Л ⁺ r l   ⁺ r 2     ² ^ r l ^ r 2 ^ cos ⁽ ^ 12 )

Продифференцируем данное выражение по ε 12 , получим:

d ^ i2 ( ^£ |2 ) =        r l   • ^{( 2} • A 2     ² • ^£ 12 ) • c^{tg (a} i )   ² • r l • r 2 • sin ⁽ ^ "12 )

d ^£ i2       2 •    r 1² + r ₂ ² - 2 • r 1 • r₂ • cos ( s ₁₂ ) + r 1² • ( X 1 ₂ - e 1 ) 2 • ctg ² ( a 1 )

Очевидно, что минимальное значение функции δ12 (ε12), на графике рисунок 2 кривая 1, соответствует условию линейного касания проволок. Минимальному значению функции δ12 (ε12) соответствует некоторый угол ε12. Как известно из курса математического анализа значение производной dδ(ε12)/dε12 в этой точке должно быть равно нулю, на графике рисунок 2 кривая 2. Для этого достаточно, чтобы числитель производной dδ(ε12)/dε12 был равен нулю. На графике видно, что в окрестности своего решение производную dδ(ε12)/dε12 можно аппроксимировать прямой. Разложим числитель производной dδ(ε12)/dε12 в ряд Тейлора teilor2(ε12) со степенью старшего члена равного 1, в окрестности точки ε12:

teilor2( £_u ) = 2 • r 1 • r ₂ • sin ( f 1 ₂ ) +

2 • r 1 ² • ctg ² ( a 1 ) + 2 • r • r ₂ • cos ( f ₁₂ ) ) • ( ^ 12 - £ 12 ) -

— ^r • ( 2 • ^ 12 ^- 2 • ^£ 12 ) • ctg ^{( a} 1 )

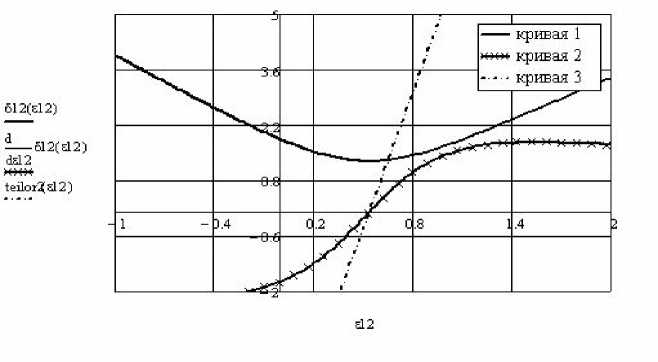
Рис. 2. Графики функций δ 12 ( ε 12 ), dδ ( ε 12 )/ dε 12 , teilor 2( ε 12 )

В качестве точки, в окрестности которой производится разложение производной функции dδ ( ε 12 )/ dε 12 в ряд Тейлора, выбрана точка

ε 12 , вычисленная с использованием выражения (6). Приравняем уравнение (10) к нулю и запишем его решение в следующем виде:

^ 2 • r i - r 2 • tg 2 ( « 1 ) • sin ( ^ 12 ) + r 2 • ⁸ 12 • tg 2 ( « 1 ) • cos ( ^ 12 )

r 2 • cos ( ^ 12 ) • tg 2 ( « 1 ) + r 1

После преобразований получим:

^ 2        - sin (^ ) + 8 12 • COs ( f 1₂ )

tg(a1 )• tg(«2 )       V cos ( 812 ) +

^V '   tg ( « 1 ) • tg ( « 2 )

Проиллюстрируем уточнение решение на примере слоя проволок каната линейного касания, изображенному на рисунке 3, со следующими параметрами: r 1 =1,75 мм, r 2 =1,75 мм, α 1 =0,785 рад, α 2 =0,785 рад, λ 12 =1,0467 рад.

Рис. 3. Слой проволок каната линейного касания

После выполнения расчетов абсолютная ошибка вычисления угла ε 12 с использованием выражения (6) составила Δ ε 12 = 0,012 рад = 0,723^о, а при использовании формулы (12) Δ ε 12 = 0,00002 рад = 0,001^о. Эталонное значение угла ε 12 определялось с использованием метода секущих и составило ε 12 = 0,5364367 рад.

Выводы: полученная формула (12) позволяет произвести уточнение решения трансцендентного уравнения (5) и может быть использована при выполнении практических расчетов. Кроме этого данная формула может использоваться при расчетах новых или нестандартных конструкций канатов линейного касания. В частности, формула (12) применялась авторами при построении моделей канатов линейного касания и последующем численном анализе напряженно-деформированного состояния.