Развитие методики выбора эффективных проектов на базе модифицированного МАИ через расширения критериальной базы и аппарата математической статистики

В статье предлагаются очередные дополнения, которые развивают методику выбора эффективных проектов через модификации метода анализа иерархий (МАИ). За счет модификаций, МАИ уже существенно изменил свою структурносодержательную суть – это выражается в сокращении недостатков, исключении противоречий, и в конечном счёте преодоления ограничений [12]: вместо целочисленной шкалы [1; …; 9] предложена дробно численная [0; …; 8]+1 – это позволяет повысить точность измерений и различить почти одинаковые объекты в форме матричных оценок; матричные оценки не выставляются экспертами в поля матриц («вслепую»), а вычисляются через специальную формулу (в том числе см. ф. 11) на базе искусственных, нечетких и детерминированных измерений объектов иерархии; показатель отношения согласованности может быть дополнен или заменён на разные критерии математической статистики для проверки согласованности экспертных суждений; преодолено максимальное количество объектов в матрице, их уже не 7–9, а любое количество; преодоление эффекта «Rank Reversal» («Эффект изменения рангов»); др.

Ранее известно, что методика состоит из ядра, двух и ещё одного фундаментального положения.

• 1.    Ядром методики является иерархия проблемы выбора эффективных проектов на базе метода анализа иерархий (AHP – Analytic Hierarchy Process), рисунок 1. Иерархия является универсальной, ограничений в количестве уровней и объектов нет.

  

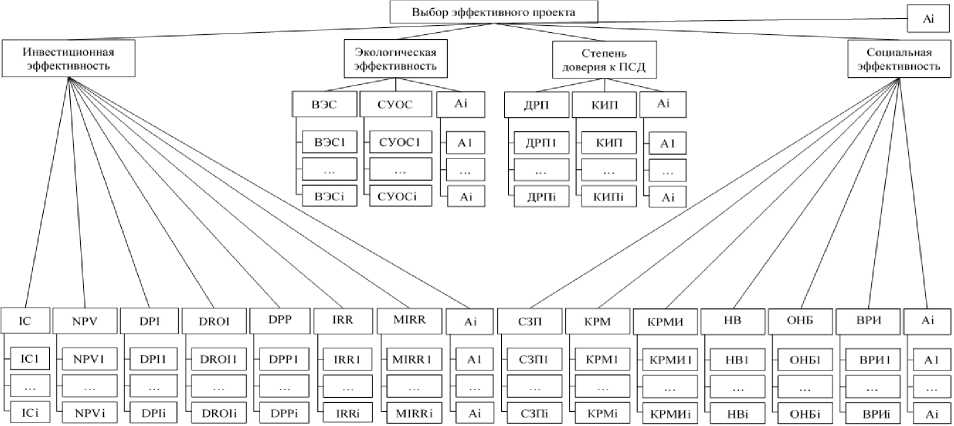
  Рисунок 1. Иерархия проблемы выбора эффективного проекта

  
  

• 2.    Положение один, содержащее признаки научной новизны: синтез МАИ с методами математической статистики (AHPMS – Analytic Hierarchy Process and Mathematical Statistics) [12, 13]. Развивается в данной статье посредством дополнения модификацией: AHPMS(AM) – М1.N (Analytic Hierarchy Process and Mathematical Statistics (Artificial Measurement)) – аналитическая иерархия в сочетании с методами математической статистики на базе искусственных измерений. Искусственные измерения объектов, как правило, это балльные экспертные оценки по какой-либо принятой численной шкале. К искусственным измерениям прибегают тогда, когда объекты не привязаны к каким-либо единым измерителям (показателям) и измерениям (единицам измерения) [12]. Например, объекты уровня 2 и 3

• 3.    Положение два, содержащее признаки научной новизны: синтез МАИ с методами теории нечётких множеств и методами математической статистики (FAHPMS – Fuzzy Analytic Hierarchy Process and Mathematical Statistics) [12, 13].

• 4.    Положение три, содержащее признаки научной новизны: классификатор AHPDD-М1.N (Analytic Hierarchy Process and Determine Data – Modification) – аналитическая иерархия в сочетании с детерминированными данными. Это единственная в своём роде модификация МАИ, которая позволяет полностью исключить влияние человеческого фактора в форме экспертных

Figure 1. Hierarchy of the effective project selection problem

требуют искусственных измерений, т. к. наименования групп и самих критериев действительно не содержат единых измерителей и измерений в отличие от объектов уровня 4 (рисунок 1).

суждений на результаты исследования за счёт привязки объектов иерархии в границах матриц парных сравнений к единым измерителям (разные показатели) и единым или смежным измерениям (единицы измерения). В полной мере позволяет решать суперзадачи разного ранга сложности в исследованиях, при условии, что опытные данные не вызывают сомнений у разных участников и заказчиков исследования, отличаясь высокой степенью достоверности и доверия к ним [12].

Первая цифра после символа «М» (Modification / модификация) обозначает принадлежность классификатора к первому поколению модификации МАИ «1». Второе поколение модификаций, которое будет существенно отличаться от первого обозначим цифрой два «2». Вторая цифра после символа «М» обозначает порядковый номер комбинации «N», всего их девять.

Результаты исследований [13] позволили определить эталонную комбинацию из девяти предложенных для классификаторов МАИ в первом поколении модификаций: AHPMS-М1.9; AHPMS(AM) – М1.9; FAHPMS-М1.9; AHPDD-М1.9, отличительными признаками которых являются: шкала дробночисленная [0; …; 8]+1 в восьми основных интервалах измерения; соблюдаются условия a d = 0 + 1 = 1 (d - diagonal - диагональные матричные оценки) и a nd = 0 + 1 = 1 (nd - not diagonal – не диагональные матричные оценки), если сравниваемые объекты Ai(j)=Aj(i); условия обратно-симметричных матричных оценок соблюдается в полной мере – 1 / a^d и 1 / a^nd ; др. новые решения и рекомендации применительно к комбинации девять. Пока в дальнейших прикладных исследованиях будем придерживаться эталонной 9-й комбинации.

В данной статье уделяется особое внимание модификации МАИ через расширение критериальной базы и возможности оценки согласованности экспертных суждений при помощи аппарата математической статистики в методике выбора эффективных проектов, в том числе через первые два фундаментальных положения и ядра. При этом следует понимать, что:

• 1.    Большая часть модификаций направлена на повышение точности и вариативности измерений, а также подтверждение согласованности экспертных суждений при оценивании именно матричных оценок.

• 2.    Остальные известные процедуры промежуточных (нормирования, собственное число матрицы и однородность суждений) и конечных вычислений (локальных и глобальных векторов приоритетов с учетом аддитивный свертки в операции иерархического синтеза) в МАИ

остаются без изменений. Эти процедуры известны, и нет смысла их повторять [10].

Все описанные в статье очередные модификации дифференцированы на разделы.

• 1.    Развитие методики выбора эффективных проектов новой категорией супермаркета для расширения критериальной базы ядра

Иерархия на рис. 1 является 4-х уровневой: уровень 1 – вершина – выбор эффективного проекта; уровень 2 – наименование групп критериев; уровень 3 – наименование критериев в виде показателей; уровень 4 – наименование критериев в виде конкретно измеряемых показателей проектов. Эти критерии уже представлялись автором. Для ознакомления с расшифровкой этих критериев следует обратится к источнику [12], затем в списке литературе найти номер 17. В данной статье нет возможности дать прямую ссылку на этот источник в связи с ограничениями, заданными редакцией журнала.

Критерии могут быть изменены, заменены и дополнены по следующим причинам:

• 1)    индивидуальные характеристики или особенности сравниваемых проектов;

• 2)    недостаточность опытных данных в проектно-сметной документации (ПСД);

• 3)    требования заказчиков и / или требования др. заинтересованных сторон исследования;

• 4)    объективные пожелания экспертов, которые непосредственно реализуют методику выбора эффективных проектов;

• 5)    какие-либо др. причины.

• 2.    Развитие методики выбора эффективных проектов новой категорией

Таким образом, условно безразмерная иерархия, позволяющая включить условно неограниченное количество разных критериев (объектов – Ai), делает методику универсальной и вполне справедливо позволяет сформулировать для неё новую категорию «Супермаркет Критериев» (Supermarket Criteria). Критерии для иерархии выбирают и принимают эксперты, а также другие заинтересованные лица в исследовании.

Помимо указанных критериев (рисунок 1), база супермаркета критериев может пополняться из разных научных источников [2, 4, 18, 20].

«Супермаркета Статистики» для дальнейшей модификации МАИ

Следующая новая категория для методики – это «Супермаркет Статистики» (Supermarket Statistics). Эта категория позволит заказчикам, пользователям и др. заинтересованным сторонам в реализации методики выбора эффективных проектов использовать разные статистические критерии оценки согласованности экспертных суждений.

Ранее автор интегрировал в методику критерий Кендэла, Пирсона, Джини и Колмогорова–Смирнова [12, 13], остались без внимания критерии Крамера–Мизеса–Смирнова, Ватсона, Андерсона–Дарлинга, Купера, Романовского, Ястремского и др. Эти статистические критерии выбраны не случайно, а по следующим причинам:

• 1)    указанные критерии более 20–30 лет в отличие от др. активно используются в науке, теории и практике социально-экономикоуправленческих направленностей, особенно при работе с экспертными оценками;

• 2)    ввиду первой причины эти критерии стали простыми, универсальными и общепринятыми нормами в науке для обработки опытных данных, полученных в социологических, экономических, управленческих и др. экспериментах;

• 3)    уточнение второй причины о простоте исполнения некоторых критериев (Ястремского, Романосвкого, Джини и Кендэла), которая заключается в отсутствии необходимости использования вспомогательных таблиц для сравнения эмпирических данных с теоретическими (табличными) и в то же время достаточно высокой их мощностью.

Далее предлагается уделить особое внимание интеграции статистических критериев Купера, Ватсона, Андерсона–Дарлинга, Крамера– Мизеса–Смирнова, Ястремского, Романовского и др. в МАИ для расширения первого и второго фундаментального положения методики выбора эффективных проектов через введённую новую категорию «Супермаркет Статистики».

Критерий омега квадрат ( ω ² ) сформулирован благодаря совместным усилиям известных математиков Х. Крамера [17], Р. Мисесс [21] и Н.В. Смирнов [11, 22]. В критерии ω ² расстояние между гипотетическим и истинным распределениями рассматривают в квадратичном измерении. Целесообразность использования критерия регламентируется условием n >  15 . Условно законченный вид формулы критерия ω ² с учётом современных требований математической статистики можно представить следующим образом:

emp fl А Г /

— + Й F ( х_; , » ) - 12 n ^1 ^V i ⁷

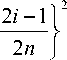
0,4  0,6"

-⁺ “ nn

х (1)

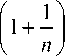
где n – объем выборки, состоящей из матричных оценок экспертов an или 1/an с учётом их ве- совых категорий; xp x2 .. xn - упорядоченные по возрастанию элементы выборки a1, a^. an или 1/ al ,1/ a2.1/ an с учётом весов (экспертные оценки), баллы; F (xi? 0) - теоретическая функция распределения критерия.

Каждому эксперту согласно определённым критериям анкеты присваивается вес 1, 2 или 3. Матричные оценки экспертов a1, a2. an и 1/ a1,1/ a2.1/ an - это и есть ранее указанные and и 1/ and . Что касается ad , то их нет смысла учитывать, т. к. это не экспертные оценки, а значения 0 +1, выставляемые при сравнении объекта с самим собой (Ai(j)=Aj(i), где i – номер строки в матрице, а j – номер столбца в матрице) по правилу обратно-симметричной матрицы.

Критерий Г.С. Ватсона [24, 25] развивает критерий Крамера–Мизеса–Смирнова. Считается, что этот критерий имеет статистический смысл при условии n >  20. Рассчитать эмпирическое значение критерия ( ) можно при помощи следующей формулы [7]:

n

,.= Z | ^F ( x » ) - i =1 V

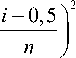
n

- n | "  Z F ( x » ) - 0.5 I + — V n 7=1              )  12 n

Чтобы уменьшить зависимость распределения статистики от объёма выборки, можно использовать в критерии модификацию следующего вида [7]:

и mo ^d . = (Vm_V - 0.1 / n + 0.1/ n ² )( 1 + 0.8/ n ) . (3)

Критерий Т.В. Андерсона и Д.А. Дарлинга [15, 16]. Этот критерий можно применять в исследовании при соблюдении условия n >  25. Вычислить значения этого критерия ( ) можно по формуле:

AD emp.

- n

—

f 2 i - 1

n

- 2z i=1

2 n

In F ( x , » ) +

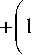
21-1 I In ( 1 - F ( x i , » ) )

В работе Н.Х. Купера «Тесты относительно случайных точек на окружности» [19] предложен критерий ( emp.) типа Колмогорова:

ememp . = D n + + D n ,              (5)

где D + = max

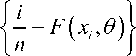
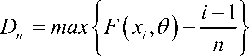
i = 1, n .

Ключевым недостатком критерия по мнению Б.Ю. Лемешко [6] является сильная зависимость распределения статистики от объема выборки. Поэтому предлагается решать эту проблему при помощи модификации критерия ( emmopd.2 ) [6, 7] на базе предложения ( emmopd.1 ) [23] следующим образом:

£-_: = А\,. |7 П + 0.155 + I , (6) V Vn;

mp ² = n^ ( d:+d - ) + Д. . (7) 3 n

В формуле 6 обозначенная проблема решается при n >  20, а в формуле 7 при n >  30.

Согласованность в методах математической статистики обычно определяют при помощи сравнения теоретических и эмпирически полученных числовых частот, выраженных в разных критериях, в форме их функций. Теоретические частоты обычно измеряются табличными (tab.) значениями, а эмпирические (emp.) частоты измеряют в ходе реализации какого-либо исследования. В результате сравнения указанных частот подтверждают простую (сложную) нулевую (Н ) или альтернативную (Н ) гипотезу с учётом уровня статистической значимости (0,1; 0,075; 0,05; 0,025; 0,01; 0,001; др.). Нулевая гипотеза подтверждается в том случае, если теоретические и эмпирические частоты схожи по числовым значениям рядов, в противном случае принимается альтернативная гипотеза.

Для подтверждения согласованности экспертных суждений aⁿ л 1 / aⁿ (Л - математическая операция конъюнкция (лингвистический эквивалент союза «и»)) в методике выбора эффективных проектов, где применяется МАИ, следует использовать простую гипотезу Н , а сложную гипотезу только в редких нестандартных или спорных ситуациях. Для проверки состоятельности простой гипотезы Н о различии теоретической и эмпирически полученных числовых частот a n л 1 / a n в ячейках матриц иерархий необходимо сравнить эмпирически полученное значение с табличными для критериев: омега квадрат “U p >  ® 2_аь. ; Ватсона Xmp. >  х_аь . ; Андерсона-Дарлинга ^mp. >  А ^Ь. ; КУпера AUOd'' ( ^'2 ) >  А,, .

Если указанное неравенство соблюдается, то следует принять гипотезу Н₁ о различии. Только в таком случае матричные оценки экспертов a n л 1 / aⁿ следует признать согласованными и принять их агрегированное значение a ag л 1 / a^ag .

В иной ситуации принимается гипотеза Н о сходстве, тогда следует признать рассогласованность экспертных оценок an л 1 / an в матрицах МАИ и статистическую несостоятельность aag л 1 / aag. Вследствие указанных действий принять или отклонить локальные и результирующие вектора приоритетов экспертов (wn и, Wn ) и их агрегированные значения (wag и Wag ).

Критерий В.И. Романовского [8,9] и Б.С. Ястремского [14] удобен тем, что не требуют обращения к таблицам распределения χ ² . Они имеют фиксированный уровень значимости p = 0,0027 [3]. Однако следует отметить, что есть формулы [1] для вычисления данных критериев, которые требуют работы со специальными таблицами для проверки статистических гипотез. Расчётные формулы критерия Романовского ( ) и Ястремского ( ) принимаются для методики выбора эффективных проектов в следующем виде [7]:

emp .

^Х emp .

2 k

у emp.

_ I X Lp . - n v2 n + 49 ’

где k - число степеней свободы; 9 - поправочная величина, принимается в размере 0,6, если n <  20.

Основная расчетная формула критерия χ² в интерпретации исследования выглядит следующим образом [5]:

s xemp.    / 1

i = 1

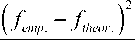
f theor .

где f – эмпирическая частота в форме матричных оценок a n л 1 / a n в МАИ, выставленных экспертами с учётом весовых категорий по шкале [0; …; 8]+1, баллы; f_theor. – теоретическая частота в форме равного распределения матричных оценок a n л 1 / a n с учётом весовых категорий экспертов в МАИ по шкале [0; …; 8]+1, баллы; s – количество разрядов признака в форме шкалы [0; …; 8]+1.

При этом для формулы 10 - k = s - r, где s – число разрядов признака в форме шкалы [0; …; 8]+1 (при этом, если в какой-либо разряд признака не попали экспертные суждения, то этот разряд исключается из вычисления критериев), а r – сумма числа параметров теоретического закона распределения. Для нормального распределения признака обычно принимают r = 3 .

Простая альтернативная гипотеза Н о различии теоретической и эмпирической частоты принимается в том случае, если соблюдается условие T^_emp (3^_тр) >  3. Только при соблюдении данного неравенства можно признать согласование экспертных оценок a n л 1/ a n в матрицах МАИ на уровне статистической значимости 0, 0027 для методики.

Кроме указанных причинных критериев попробуем максимально расширить новую для методики категорию супермаркета статистики при помощи следующих критериев на базе трудов А.И. Кобзаря [5] и Б.Ю. Лемешко и др. [7]:

• 1)    общих согласия: числа пустых интервалов; квартильный Барнетта-Эйсена; Реньи; Дарбина; др.;

• 2)    проверки нормальности распределения: модифицированный медианный; модифицированный вероятностный; Катценбайссера-Хакля; Фроцини; Шапиро–Уилка; Васичека; Хегази– Грина; Али–Чёрго–Ревеса; Филлибена; Ла Брека; Локка–Спурье; Оя; Гири; Дэвида-Хартли– Пирсона; Шпигельхальтера; Саркади; Лина– Мудхолкара; Мартинеса–Иглевича; ДʼАгостино; асимметрии и эксцесса; Муроты–Такеучи; др.;

• 3)    проверки экспоненциальности распределения: Шапиро–Уилка; Колмогорова–Смирнова; корреляционной экспоненциальности; регрессионный Брейна–Шапиро; Кимбера–Мичела; Фишера; Бартлетта–Морана; Климко-Антла– Радемакера–Рокетта; Холлендера–Прошана; Кочара; Эппса–Палли–Чёрго–Уэлча; Бергмана; Шермана; Колмогорова–Смирнова наибольшего интервала; Хартли; показательных меток; ранговый независимости интервалов; Ю в разных вариантах; Гринвуда; Манн–Фертига–Шуера для распределения Вейбулла; Дещнанде; Лоулесса; др.;

• 4)    согласия для равномерного распределения: Шермана; Морана; Ченга–Спиринга; Саркади–Косика; Дудевича-ван дер Мюлена; Хегази–Грина; Янга; Фроцини; Гринвуда– Кэсенберри–Миллера; «Сглаженный» Неймана-Бартона; др.;

• 5)    симметрии: «быстрый» Кенуя; Смирнова; знаковый; одновыборочный Вилкоксона; Антилла–Керстинга–Цуккини; Бхатачарья– Гаствирта-Райта; Финча; Бооса; Гупты; Фрезера;

• 6)    не указанные с учётом их всевозможных модификаций.

• 3. Развитие методики выбора эффективных проектов посредством расширения возможностей оценки согласованности экспертных суждений при помощи аппарата математической статистики в МАИ

Таким образом, супермаркет статистики – это действительно супермаркет, который позволяет выбрать пользователям методики более 76 критериев, при помощи которых можно оценить уровень согласованности экспертных мнений в форме a n л 1/ a n для принятия или отклонения a Og л 1/ a ag , w” , w ag , W ” и W^ f .

ij ij Ai Ai Ai Ai

Технологию расчёта некоторых критериев пользователям нужно будет адаптировать под методику или др. область научного исследования, но это лишь определённые действия по интеграции выбранных критериев, которые нужно будет делать в процессе самого исследования.

Если предположить, что в иерархии (рисунок 1) четыре уровня, в первых 3 из которых более 26 объектов (с учётом объектов Ai), исключая вершину, а на четвёртом уровне более 63 объектов (с учётом объектов Ai и тех, которые отмечены многоточием), то получится более 128 матричных оценок без учёта и 256 с учётом качества обратной-симметрии матриц. При этом диагональные оценки – a ^d не должны учитываться в указанных данных, а не диагональные - a nd ^ a n , напротив, должны учитываться, даже при условии Аi(j)=Аj(i))! Далее, если предположить, что в методике можно использовать более 76 статистических критериев оценки согласия экспертных суждений, то получится без учёта и с учетом обратной симметрии матриц более 9728 (128 х 76) или более 19456 (256 х 76) оценок. В завершение, если учесть, что подавляющее большинство статистических критериев из числа 76 позволяют проводить оценивание минимум на двух уровнях статистической значимости (обычно 0,05 и 0,01), то получится удвоенное значение возможных оценок согласованности экспертных мнений в методике более 19456 и более 38912. Получится колоссальный масштаб исследования, который можно охарактеризовать ещё одной новой категорией «Полигон Статистики» (Statistics Polygon) для методики выбора эффективных проектов.

В процессе реализации методики будет вполне достаточно выбрать из супермаркета статистики 1–2 критерия для подтверждения согласованности экспертных суждений в виде матричных оценок.

Описанная категория супермаркета статистики позволит заказчикам, пользователям и др. заинтересованным лицам в реализации методики выбора эффективных проектов и в др. областях науки выбирать и использовать разные статистические критерии оценки согласованности экспертных суждений:

• 1.    В матричных оценках иерархии – a n л 1 / a n для классификаторов AHPMS-M1.9, AHPMS(AM) – М1.9 и FAHPMS-М1.9.

• 2.    В измерениях самих объектов иерархии – Ai для классификаторов AHPMS(AM) – М1.9 и FAHPMS-М1.9.

Т.к. первое фундаментальное положение изначально ориентировано на проверку статистической значимости экспертных суждений, выраженных в форме матричных оценок, то продолжим придерживаться этого ориентира, выраженного в пункте 1. Кроме того, принятый ориентир отличается высокой определённостью разрядов признака для некоторых критериев математической статистики (например Пирсона и Колмогорова-Смирнова), согласующихся с ранее принятой эталонной девятой комбинацией первого поколения модификаций МАИ: шкала дробночисленная [0; …; 8]+1 в восьми основных интервалах измерения; классификаторы

AHPMS-М1.9, AHPMS(AM) – М1.9 и FAHPMS-М1.9. Представим разряды признаков для реализации оценки согласованности экспертных суждений по некоторым критериям математической статистики с учётом обновления для девятой комбинации первого поколения модификации МАИ в таблице 1.

В результате максимально возможное количество разрядов признака для матричных оценок для М1.9 в МАИ следующие: 17 – для высокого качества исследования, где у a^П л 1/ a n разряд «1» общий; 9 – для низкого качества исследования. При необходимости качество исследования можно ещё повысить за счёт дифференцирования указанных 17 разрядов признака.

Таблица 1. Представление разрядов признака для реализации оценки согласованности экспертных суждений разного качества по критериям математической статистики типа Пирсона, Колмогорова-Смирнова и др. для М1.9 (шкала дробночисленная [0; …; 8]+1) первого поколения модификаций МАИ

Table 1.

Representation of attribute digits for the implementation of the assessment of the consistency of expert judgments of different quality according to the criteria of mathematical statistics such as Pearson, Kolmogorov-Smirnov, etc. for M1.9 (fractional scale [0; …; 8] + 1) of the first generation of AHP modifications

Для проверки aag через согласованность an , баллы | For ag                           n check a    through consistency a , points		Для проверки 1 / aag через согласованность 1 / an , баллы | For check 1 / aag through consistency 1 / an , points
Количество разрядов признака для методов математической статистики* | The number of attribute digits for methods of mathematical statistics*
9	5	9	5
1	1	1	1
1–1,9999	1–2,9999	1–0,5000	1–0,3333
2–2,9999		0,4999–0,3333
3–3,9999	3–4,9999	0,3332–0,2500	0,3332–0,2000
4–4,9999		0,2499–0,2000
5–5,9999	5–6,9999	0,1999–0,1667	0,1999–0,1429
6–6,9999		0,1666–0,1429
7–7,9999	7–9	0,1428–0,1250	0,1428–0,1111
8–9		0,1249–0,1111
Уровень качества исследования методами математической статистики согласованности экспертных суждений для методики | The level of research quality by methods of mathematical statistics of the consistency of expert judgments for the technique
высокое | high	низкое | low	высокое | high	низкое | low
Рекомендуемый средний размер выборки из генеральной совокупности для возможности получения достаточного уровня согласования экспертных суждений с учётом весовых категорий через критерии из супермаркета статистики, соответствующей выражению m П = /    VM из формулы 12** ^■^^ П= 1 Recommended average sample size from the general population to be able to obtain a sufficient level of agreement between expert judgments, m taking into account weight categories through criteria from the statistics supermarket corresponding to the expression П = /     V from the П = 1 П formula 12**
от 18–20 | from 18–20	от 12–14 | from 12–14	от 18–20 | from 18–20	от 12–14 | from 12–14

Примечание: *Не ко всем критериям математической статистики из супермаркета требуется представление разрядов признаков **Размер выборки может быть изменён из-за особенностей применения некоторых критериев математической статистики или условий в исследовании, в том числе и с учётом уровня значимости статистики (0,1; 0,075; 0,05; 0,01)

Note: *Not all criteria of mathematical statistics from the supermarket require the presentation of feature digits **The sample size can be changed due to the peculiarities of applying some criteria of mathematical statistics or conditions in the study, including taking into account the level of significance of statistics (0.1; 0.075; 0.05; 0.01)

Напомним, что оценки ad не учитываются и не должны учитываться в указанных данных, а and ^ an, напротив, учитываются. Также следует ещё раз напомнить о том, что если в каком-либо разряде признака нет данных, то он исключается из исследования. Эта мера позволит технически повысить качество исследования статистики матричных оценок в МАИ.

Что касается пункта 2 – «В измерениях самих объектов иерархии – Ai», то содержание его разрядов признака будет описано в др. статье автора и скорее всего в контексте изложения модификаций МАИ второго поколения, где предполагается преодоление или точнее уход от эталонной дробночисленной шкалы [0; …; 8]+1 измерения матричных оценок к универсальной дробночисленной в границах минимум-максимум измерения Ai-х объектов в матрице иерархии.

В конечном счёте указанные два пункта и новая категория супермаркета статистики позволят проверять и перепроверять необходимое количество раз an л 1/ an и Aij для подтверждения или опровержения статистической значимости агрегированных матричных оценок aag л 1/ aag, локальных wag и результирующих Wag векторов приоритетов в иерархии или семействе иерархий для методики выбора эффективных проектов. А также при определённых автором условиях [12] заменять или дополнять показатель ОС/CR (отношение согласованности/Consistency Ratio).

На основании данных, описанных в табл. 1, аналитическое выражение индивидуальных экспертных оценок a n л 1/ a n , полученных при помощи попарного сравнения матричных объектов Аi(j) по формуле 11 для определения их агрегированных значений a^ag л 1/ a^ag по формуле 12 в границах полной 17-балльной шкалы, можно представить в виде формулы 13:

а n A ( j )- Aj ( i )| = ij          SS

I ^{Ai ( j )- Aj (} i )l

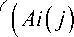
— ^{Ai ( j} ) min . )

+ 1 e [ 0; _ ;8 ] + 1, М 1.9,

Z m n a ⁿ v n = 1 ^j n

Em n=Vn aag v 1/aag =<

V

,

^m 1/ a ⁿ v

Z—tn =Д у) ⁿ

Zm n=1vn

^Ai ( j ) >  А ( i ) ^ a in eV [ 0; _ ;8 ] + 1

V an v 1/ an ^ Ai(j)< Aj(i)^ 1/ an eV[1;...0,1111],

V

Ai ( j ) = Aj ( i ) ^ a d = a n = 0 + 1 = 1

где an и 1/an – субъективная матричная оценка и её обратное значение, принадлежащая i-й строке и j-му столбцу, выраженная при помощи эксперт- ного суждения – n, для повышения точности измерений в формуле 11 рекомендуется округлять эту оценку до десятитысячных или стотысячных, баллы; Ai (j) и Aj (i) - объекты матрицы! парных сравнений, измеряемые в каких-либо единых единицах измерения при помощи каких-либо единых или смежных измерителей, ед. изм.; SS – Step of the Scale – это расчётный шаг шкалы, для повышения точности измерений ре- комендуется его округлять до десятитысячных или стотысячных, баллы; Ai ( i) и Ai ( j)   - max.               min.

максимальное и минимальное измерение объектов матрицы парных сравнений из числа её объектов Ai (j) в каких-либо единых единицах измерения при помощи каких-либо единых или смежных измерителей, баллы; 8 – очень сильное предпочтение по шкале Т. Саати, баллы; +1 – необходимое действие в формуле 11 для комбинаций М1.9 чтобы избежать грубых ошибок из- мерения и получения возможности корректного вычисления показателя согласованности мат- ричных оценок при соблюдении определённых условий в модифицированном исполнении МАИ; М1.9 – сокращённое название принятых эталонных классификаторов (AHPMS(AM) – М1.9 и FAHPMS-М1.9) первого поколения модификаций МАИ, принадлежащих «∈» дробночисленной шкале [0; …; 8]+1; v – весовая оценка эксперта – n;

m – количество множителей; n – порядковый номер эксперта;

E m

v n=1 n

– сумма всех весов экс-

пертов (веса экспертов могут быть 1, 2 или 3); ∀ – математическая операция квантор общности (лингвистический эквивалент «любой», «всякий» и т. д.), подразумевает возможность получения любого дробночисленного измерения an v 1/ an в диапазонах [0;^;8] +1 v[1;_0,1111] через формулу 11; ad и and – диагональная (d – diagonal) и не диагональная (nd – not diagonal) матричные оценки, соответствующее им значение «0+1» или «1» балл при соблюдении равенства Ai (j) = Aj(i) для всех классификаторов М1.9;

∨ – математическая операция дизъюнкции (лингвистический эквивалент «или»), необходима для выбора действий; ⇒ – в математической логике этот символ используется для обозначения бинарной логической связи, по своему применению приближенная к союзам «если…, то…», чаще всего импликация записывается как посылка или следование к чему-либо.

Указанные три действия на выбор в формуле 13 дают возможность оценивания an v l / an для 9-ой комбинации первого поколения модификаций МАИ, указанных классификаторов AHPMS(AM) – М1.9 и FAHPMS-М1.9 через использование дробночисленной шкалы [0; …; 8]+1 с восемью основными интервалами измерения. Кроме того, an вычисляется согласно формуле 11 [12, 13], её обратная оценка вычисляется по стандартному правилу МАИ – 1 / an . Для корректного использования указанной формулы 11 из источника [12] прилагаются подробные инструкции, правила, условия и т. д. по её применению в стандартных и нестандартных случаях.

Для проверки согласованности оценок a n л l / a n , образующих числовой ряд в числителе

Em n      m   n n=layvn ЛLn=ll/aчvn формулы 12, следует использовать критерии математической статистики, выбранные из супермаркета статистики для дальнейшего принятия или отклонения aag л l / aag, wa®, Wgg, управленческих решений четырёх порядков. Следует напомнить о том, что значения an л l / an принимаются в количестве равном весовой категории эксперта. Например, присвоена весовая категория матричной оценки первого эксперта (al = 5 баллов, а l / al = l / 5) в размере три (v=3), тогда правильная запись этой матричной оценки в числовом ряду будет выглядеть следующим образом:

1             1.1    1.2    1.3               1                  1.1          1.2          1.3

ay ^ г1- ;a4 ;a4 }лl/ay ^i1 a- ;l/ay ;l/ay} ;  al ^{5;5;5}лl/al ^{l/5;l/5;l/5} . Если упростить восприятие, то матричная оценка al л l / al из примера должна приниматься в форме трёх одинаковых оценок вместо одной для полного представления числового ряда. Таким образом, размер выборки для математической статистики следует определять путём суммирования всех весовых категорий, принадлежащих m экспертам в группе: n = Evn . i=l

Ввиду описанной сути представления формулы 12 и 13 дополнительно отметим, что эксперты для определения матричных оценок работают в поле матрицы только в случае классификатора AHPMS-М1.N, т. к. в нём объекты иерархии в матрицах не привязаны полностью или частично к единым измерениям и единым / смежным измерителям. Во всех остальных указанных классификаторах:

• 1)    AHPMS(AM) – М1.N эксперты только искусственно чётко или при необходимости нечётко измеряют объекты иерархии в матрицах по какой-либо принятой единой искусственной шкале, в самой матрице они не работают, а все

матричные оценки вычисляются при помощи формулы 11;

• 2)    FAHPMS-М1.N эксперты только выбирают измерения в заданных нечётких интервалах объектов иерархии в матрицах или выбирают способ конвертирования нечёткого числа в чёткое [12], в самой матрице они не работают,

а все матричные оценки вычисляются при помощи формулы 11.

Результаты исследования всей иерархии или семейства иерархий в форме локальных wag и результирующих W^® векторов приоритетов следует признать статистически значимыми и принять в том случае, если показатель УРСР – уровень результирующей согласованности решений (RCSL – Resulting Compatibility Solution Level), согласно вербально-числовой шкале Е. Харрингтона, определён в диапазоне 0,8–0,1 – очень высокая оценка – «консенсус экспертных суждений» при объёмной выборке экспертов более 15–20 человек с учётом их весовых категорий. Если число экспертов едва ли больше 9–10 человек, то рекомендуется ориентироваться на диапазон 0,64–0,79 – высокая оценка – «компромисс экспертных суждений», при этом сле- дует понимать, что желательно стремиться к значению близкому к 0,79.

Формула вычисления RCSL для одной иерархии (Ahi) выглядит следующим образом:

1 AhiLimAi ад

* i=j=i     ^a ij

'AhiLimAi  ад ,

‘ i=j=i     ^a ij

RCSLAhi

vAhiLimAi d /ад

^i=j=1    X/Uj, х  vAhiLimAi d „ ад ,   \   /

L i=j=i     1/^a ij

V AhiLimAi ад Л1 , ад

L i=j=i     ^a ij ^^1/a ij

• ¹   _v AhiLimAi ад .^a g ,

L i=j=t     ^a ij ^^1/a ij

AhiLimAi       AhiLimAi             AhiLimAi где E aag,  £ l/aag и E aagлl/aag- i=j=l              i=j=l                     i=j=l сумма количества самих матричных оценок (не численных их значений) из всех матриц и уровней иерархии, не прошедших проверку по статистическим критериям, логически отрицаемые AhiLimAi       AhiLimAi

(черта над символом); E a a , E 1/ a^ag и ¹ = j = ^{l              1} = J = ^l

AhiLimAi

E aaag л l / aaag - сумма количества самих i=j=l матричных оценок (не численных их значений)

из всех матриц и уровней иерархии;      матрице (m – matrix), принадлежащей объекту

AhiLimAi – принадлежность агрегированной      Ai в иерархии.

матричной оценки к определённой i-ой иерархии            Диапазоны измерений показателя RCSL

(Ah – Analytic hierarchy), i-му уровню (Li – Level) и       даются в таблице 2.

Таблица 2.

Шкала определения RCSL для методики выбора эффективных проектов

Table 2.

RCSL definition scale for effective project selection methodology

Шкала Е. Харрингтона              Шкала определения RCSL экспертов для МАИ и методики

E. Harrington scale                     Scale for determining RCSL experts for AHP and methods

Вербальные характеристики       Числовые характеристики Verbal characteristics               Numerical characteristics	Вербальные характеристики Verbal characteristics
Очень высокая оценка Very high rating                          0,8–1	Консенсус Consensus
Высокая оценка high rating                          0,64–0,79	Компромисс Compromise
Средняя оценка                     0 37–0 63 average rating                             ,     ,	Конфликт средней тяжести Medium conflict
Низкая оценка НиLзoкwаяrоatцiеnнgка                       0,2–0,36 Очень низкая оценка Very low rating                         0–0,19	Конфликт высшей тяжести Conflict of the highest severity

Для корректного использования формулы 14 рекомендуется выполнять следующие действия для статистической проверки w ^ag и W ^ag : в расчёт берутся только aⁿ ; в расчёт берутся только 1/ aⁿ ; в расчёт берутся aⁿ и 1 / aⁿ ; во всех указанных случаях не учитываются a^d , они должны исключаться.

Следует также отметить, что показатель RCSL можно вычислять для каждой матрицы в иерархии отдельно ( RCSL ), для нескольких матриц, находящихся на одном (разных) уровне (уровнях) иерархии (RCSL umA^-LimAn ) или даже для всего уровня иерархии ( RCSL ), уровней (RCSL_Li ,_Ln). При необходимости можно вычислить RCSL для двух и более, вплоть до всего семейства иерархий, обозначение будет иметь следующий вид RCSL . В указанных классификаторах под «n» следует понимать только конечный порядковый номер для матриц, уровней и иерархий.

При этом формула 14 не изменит свой аналитический вид, а отличием во всех этих случаях будет только граница входных данных – одна матрица, несколько матриц и все матрицы, относящиеся к одному, нескольким и более уровням иерархии в различных сочетаниях.

Все описанные действия по применению формулы 14 дают возможность использования классификации управленческих решений четырёх порядков для методики выбора эффективных проектов с возможностью их адаптации для др. областей науки. Формулы этих решений уже представлялись автором. Для ознакомления с этими формулами следует обратится к источнику [12], затем в списке литературе найти номер 18. В данной статье нет возможности дать прямую ссылку на этот источник в связи с ограничениями, заданными редакцией журнала.

Заключение

В данной статье автор продолжил научный путь в области развития методики выбора эффективных проектов для теории и практики инвестиционного менеджмента и управленческих решений. Полагается, что на практике методика позволит заинтересованным сторонам оценивать и выбирать эффективные проекты для развития экономических и других субъектов на разных уровнях экономики и управления.

Получены следующие результаты, которые отличаются научной новизной:

• 1)    введен классификатор AHPMS(AM) – аналитическая иерархия в сочетании с методами математической статистики на базе искусственных измерений;

• 2)    предложен классификатор AHPDD – аналитическая иерархия в сочетании с детерминированными данными;

• 3)    добавлены категории «Супермаркет Критериев» и «Супермаркет Статистики»;

• 4)    представлена формула вычисления RCSL (уровень результирующей согласованности решений).

Указанные результаты позволят:

• 1)    сократить или исключить человеческий фактор субъективизма из исследования за счет пункта 1 и 2;

• 2)    дополнить или полностью заменить показатель отношения согласованности матричных оценок за счет пункта 1;

• 3)    выбирать любое количества критериев оценки объектов в иерархии и выбирать 1, 2 или более критериев математической статистики для оценки согласованности экспертных суждений, за счет пункта 3;

• 4)    принимать условно любое количество объектов на уровнях иерархии, за счет указанных положений и вычисления матричных оценок по формуле 11;

• 5)    оценивать общую согласованность экспертных суждений по иерархии или семейству иерархии за счет пункта 4 в сопряжении с пунктом 1.

Для полного завершения методики потребуется опубликовать еще три статьи, а для ее трансформации в методологию одна статья. В этих статьях будет уделено внимание: развитию методических положений классификатора FAHPMS (синтез МАИ с методами теории нечётких множеств и методами математической статистики); разрешения проблемы эффекта рангов; построение алгоритмов; и т. д.

Только после завершения работы над методологией появится смысл в её апробации, результаты которой будут опубликованы в свое время.