Развитие модели методологии DEA

Проблема оценки эффективности функционирования предприятий очень остро встает в последние годы во многих сферах производства и сбыта продукции. Часто возникают задачи сравнения между собой и упорядочивания структурных подразделений и предприятий или организаций в целом по некоторому свойству, не поддающемуся непосредственному измерению [1]. При этом общее представление о степени проявления анализируемого латентного свойства складывается в результате определенного суммирования целого ряда частных (и поддающихся измерению) характеристик, от которых в конечном счете зависит это свойство. Несомненно, главным понятием здесь является понятие эффективности как наиболее общего, определяющего свойства любой целенаправленной деятельности, которое с познавательной точки зрения раскрывается через категорию цели и объективно выражается степенью достижения цели с учетом затрат ресурсов и времени. Поэтому оценка эффективности функционирования предприятий и организаций является очень важной для принятия верных управленческих решений.

В данной статье мы будем рассматривать метод DEA (Data Envelopment Analysis) основанный на построении границы эффективности. Эта граница имеет форму выпуклой оболочки и используется в качестве эталона (точки отсчета) для получения численного значения оценки эффективности каждого из объектов в исследуемой совокупности.

По аналогии с границей эффективности можно ввести понятие границы отставания. Эта граница будет использоваться в качестве эталона для получения численного значения оценки отставания (убыточности) каждого из объектов. На пересечении двух границ будет построена гиперплоскость, разделяющая совокупность объектов на два класса.

Метод Data Envelopment Analysis. Данный метод представляет способ оценки производственной функции, которая неизвестна. Метод DEA основан на построении границы эффективности, которая и является аналогом производственной функции для случая, когда выпуск является не скалярным, а векторным, т. е. когда выпускается несколько видов продукции. Эта граница имеет форму выпуклой оболочки или выпуклого конуса в пространстве входных и выходных переменных, описывающих каждый объект в исследуемой совокупности. Из названия метода следует, что граница эффективности как бы оги- бает, или обертывает точки, соответствующие исследуемым объектам в многомерном пространстве (англ. envelopment – обертывание). Степень эффективности объектов определяется степенью их близости к границе эффективности в многомерном пространстве входов-выходов. Способом построения границы эффективности является многократное решение задачи линейного программирования.

Поясним основную идею метода DEA на примере процесса производства одного вида продукции y из двух видов ресурсов х ₁ и х ₂ [2].

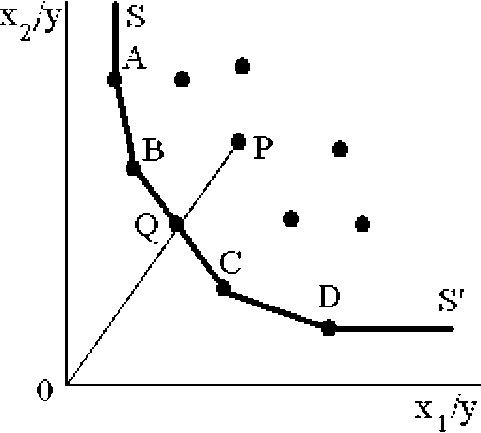
Рис. 1. Технология производства с двумя входами и одним выходом

Если считать эффект масштаба постоянным, то можно использовать двухмерный график, по осям координат которого отложены удельные затраты ресурсов, т. е. объемы ресурсов х ₁ и х ₂ в расчете на единицу выпускаемой продукции. В результате будет получена единичная изокванта (рис. 1).

Пусть объект (фирма) P использует ресурсы в объемах, соответствующих точке P на рис. 1. Тогда его техническая (технологическая) неэффективность будет выражаться длиной отрезка QP. Точка Q является проекцией точки P на границу эффективности, при этом проециро- вание производится по направлению к началу координат.

Длина отрезка QP представляет собой величину, на которую могут быть пропорционально сокращены объемы затрат ресурсов х1 и х2 без уменьшения объема выпуска y. Такой подход к определению эффективности назы- вается ориентированным на вход (input-orientated). Тогда техническая эффективность объекта (фирмы) P будет определяться таким образом:

0 Q 0 P ^.

ТЕР

Точки A, B, C и D на рис. 1 являются эффективными, поэтому на их основе и будет сформирована граница эффективности. Точка P не лежит на границе неэффективности, следовательно она не является эффективной.

Проецирование точек, соответствующих неэффективным объектам, на границу эффективности считается пра- вомерным, исходя из принципа: если объект A способен произвести определенный объем выпуска из определенного объема ресурсов, то и объект B также должен быть способен произвести такой же объем выпуска из такого же объема ресурсов.

Известно, что значение технической эффективности не может превышать единицы. При проецировании неэффективного объекта на границу эффективности для него формируется целевой гипотетический объект, который является эффективным. Этот объект в математическом смысле представляет собой линейную комбинацию реальных эффективных объектов (под реальным объектом в данном случае подразумевается точка в многомерном пространстве). Число объектов, входящих в эту комбинацию, зависит от ряда факторов, в том числе от количества входных и выходных переменных, описывающих объекты, и от значений этих переменных. Значения входных и выходных переменных целевого объекта и служат целями для неэффективного объекта.

Рассмотрим еще один пример использования метода DEA. Пусть имеются данные для K входных и M выходных параметров для каждого из N однородных объектов (такими объектами могут быть, например, фирмы, банки и т. д.) [4]. Для i -го объекта они представлены векторами-столбцами х_i и y_i соответственно. Тогда матрица X размерности K × N и матрица Y размерности M × N представляют собой матрицы входных и выходных параметров для всех N объектов. Модель формулируется в виде задачи линейного программирования в такой форме:

min _{θ , λ} ( θ ),

- y i + Y λ≥ 0, θ x_i - X λ≥ 0,

λ≥ 0, где θ – скаляр; λ – вектор констант размерности N × 1 . Значение θ , полученное при решении задачи, будет мерой эффективности i -го объекта. При этом эффективность не может превышать единицы. Аналогичная задача решается N раз, т. е. для каждого объекта.

Модель (1) построена в предположении постоянного эффекта масштаба и в результате ее N-кратного решения формируется граница эффективности в виде выпуклого конуса. Коническая форма границы эффективности обусловлена тем, что в модели (1) нет ограничения на сумму N элементов вектора λ, такого как ∑ λi =1 .

i =1

Поясним смысл вектора λ . Из выпуклого анализа известно, что каждая точка, принадлежащая выпуклому конусу, натянутому на некоторое множество точек, может быть представлена в виде неотрицательной линейной комбинации этих точек, т. е. в виде ( X λ , Y λ ). Часть элементов вектора λ имеет ненулевые значения. Эти элементы соответствуют тем объектам, которые являются эталонными для оцениваемого объекта. Линейная комбинация эталонных объектов образует гипотетический объект, находящийся на границе эффективности и являющийся проекцией реального неэффективного объекта. В ситуации, представленной на рис. 1, эталонами для объекта P являются объекты B и C , поэтому

λ≠ 0, λ≠ 0, λ≠ 0, λ≠ 0. BCAD

Те объекты, для которых значение показателя эффективности 9 оказалось равным единице, находятся на границе эффективности. Для объектов, у которых показатель эффективности 9 оказался меньше единицы, могут быть выданы рекомендации, заключающиеся в выведении таких объектов на границу эффективности за счет пропорционального сокращения объемов затрачиваемых ими ресурсов при сохранении значений выходных переменных на прежнем уровне. Поэтому модель (1) называется моделью, ориентированной на вход. Рекомендуемые значения входных переменных рассчитываются по формуле убыточные или отстающие от основной части выборки объекты.

По аналогии с [2] возьмем отношение всех входов ко v' xi всем выходам для i-го объекта     , где u – вектор весов u' yi для выхода размерности M х 1; v - вектор весов для входа размерности K х 1. Чтобы выбрать оптимальные веса, сформулируем задачу математического программирования:

хрек =9 xi, где 9 - показатель эффективности i-го (неэффективного) объекта; xi – вектор значений входных переменных для i-го объекта.

Представим модель, аналогичную модели (1), но построенную в предположении переменного эффекта масштаба:

min ед ^{( 9 )},

- y + Y X> 0,

9 xi- X X> 0,

N ух,= 1,

=1

х> 0.

При решении этой задачи формируемая граница эффективности имеет форму выпуклой оболочки, посколь-N ку вследствие наложения условия EXi = 1 гипотетичес- i=1

кие объекты ( X X , Y X ) равны выпуклой линейной комбинации эффективных точек (рис. 2).

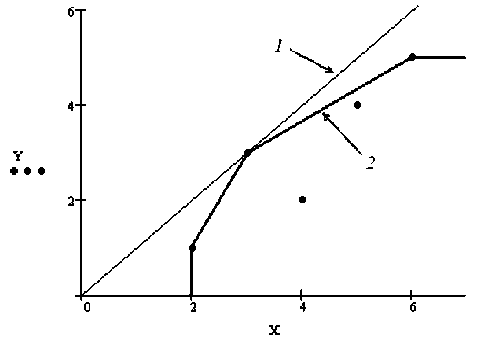
Рис. 2. Модель, построенная в предположении постоянного эффекта масштаба ( 1 ), и модель, построенная в предположении переменного эффекта масштаба ( 2 ), для одной и той же совокупности объектов

Граница отставания и разбиение выборки на два класса. Рассмотрим модель метода DEA, построенную в предположении переменного эффекта масштаба (2).

Граница эффективности огибает точки, соответствующие эффективным объектам. Теперь построим такую же границу, но наоборот. Назовем ее границей отставания (убыточности). Граница отставания будет показывать

Это потребует нахождения таких значений u и v , чтобы мера отставания (убыточности) i -го объекта была максимальной при условии, что ограничение должно быть меньше или равно единице. Тогда возникает проблема, связанная с особенностью формулировки задачи, которая приводит к бесконечному множеству решений. Чтобы избежать этого, можно наложить ограничение.

Введем ограничение u ' y i = 1 и получим: ^max H,v ( v ' x i ) ’

Ц' yi = 1, v' Xj-ц' yj< 0, j = 1,2,..., N,

Ц, v> 0.

Найдем двойственную к ней задачу:

^min 9,X ^{( 9 )},

9 y , .- Y X> 0,

— x i - X X >  0,

X> 0.

Добавим ограничение на сумму элементов вектора N

• X : E X i = 1. Тогда модель границы отставания будет

miⁿ 9,X ^{( 9 )},

9 у , - Y X> 0,

• ^- X X ^X> °’              (3)

E X , -1,

=1

X> 0, где 9 - мера отставания (убыточности) объекта. Если 9 = 1, то этот объект формирует границу отставания и является отстающим. Показатель 9 принимает значения от 0 до 1.

Графики границы эффективности и границы отставания (рис. 3) показывают, что обе границы пересекаются в двух точках. Через их пересечение можно провести прямую, разделяющую множество объектов на два класса. Первый класс (I) – это эффективные или нормальные объекты, второй класс (II) – отстающие объекты (рис. 4).

Если распространить рассмотрение на многомерный случай, когда имеются несколько входов и несколько выходов, то разделяющей поверхностью будет гиперплоскость.

Таким образом, в данной статье был рассмотрен метод DEA, предложена и построена граница отставания, а также представлено разбиение множества объектов на два класса, что облегчает ЛПР классификацию объектов, так как предполагает существование всего двух классов: плохого и хорошего. Это удобно, когда выборка объектов достаточно велика. Если ЛПР требуется точное количественное значение эффективности, то он получает это решение из прямого решения задачи по методу DEA.