RBF-алгоритм и его модификации для построения поверхностных компьютерных 3D моделей в медицинской практике

факт, что современные средства сканирования объектов предоставляют на выходе количество точек порядка (10 ⁴ -10 ⁶ ), то использование по-лигональногопредставления становится нерациональным. Поэтому исследователи, в первую очередь, уделяют внимание получению моделей на основе поверхностного представления. Тем более что поверхностное представление по оценкам экспертов дает более реалистичные модели и позволяет легко устранять такие дефекты входных данных как неполнота, повреждения и др [2].

ЦЕЛЬ ИССЛЕДОВАНИЯ

Для получения подобных моделей существует множество подходов. Задача данного исследования – провести сравнительный анализ существующих методов и оценить возможность их применения в составе программной системы для моделирования объектов в медицинской практике [3].

МАТЕРИАЛЫ

И МЕТОДЫ ИССЛЕДОВАНИЯ

Построение модели объекта в трехмерном пространстве на основе проекционных данных

Особенностями моделей объектов непосредственно в медицинской практике являются [3]:

• -    значительное число проекционных точек (10 ⁴ -10 ⁶ ), что обусловлено особенностями получения проекционных данных, как совокупности точек контуров объектов на 2D-проекциях;

• -    повышенные требования к точности модели, что связано с необходимостью

учитывать мелкие множественные артефакты;

• - возможность построения модели в реальном времени, что связано с необходимостью учи-

• тывать динамику моделируемого объекта (например, в системах визуализации хирургических операций и т.д. [4]).

Для построения вышеуказанных моделей используются сплайны, классическая триангуляция, α -поверхности и др. Авторами уже рассматривались методы моделирования на основе сплайнового представления [5], но как было определено в [6], наиболее эффективным средством моделирования поверхностей в трехмерном пространстве является метод RBF.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В данной работе ставится задача проанализировать возможность применения различных модификаций метода RBF применительно к объектам, обладающим ранее перечисленными особенностями (большое число проекционных точек, высокая точность, реальное время).

С точки зрения метода RBF, объект (поверхность) представляется в виде:

N

/W = ^^,^(^С,),   (1)

7=1

где λ – коэффициенты; ...

ϕ – функция RBF, вычисленная для произвольной точки пространства;

c _{1... N} – заданные точки поверхности (проекционные данные).

Коэффициенты ε определяются как вектор-столбец, являющийся решением системы уравнений вида:

<Р^^сд (p(c_vc^ ... ^„Cj,) ^2^1) ^(c₂,c₂) ...

2,c_N)

*nA)

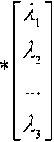
Й1

h.

где

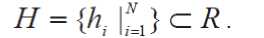
В методах получения 2D-моделей, например, в методе моделирования рельефа по изолиниям [7] значения вектора-столбца H – это значения, которые принимает искомая модель в заданных точках множества

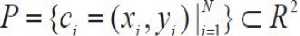
Для случая трехмерного пространства множество P принимает вид:

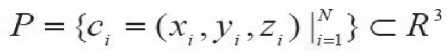
В этом случае модель объекта (поверхность) задается неявно в виде функции, принимающей некоторое оговоренное значение в каждой точке поверхности: F( . c) = const В качестве RBF можно использовать различные функции, значение которых определяется расстоянием между двумя точками пространства [8] ( см. табл. 1 ; r = x – c – радиус функции RBF).

Таким образом, процесс построения модели объекта заключается в следующем:

• -    расчет матрицы значений функции RBF для заданных точек;

• -    решение системы линейных уравнений для определения коэффициентов λ ;

Таблица 1. Радиус функции RBF

Тип функции	KBF
Piecewise polynomial (RP)
Thin plate spline (TPS)	*)=k" lnH
Multiquadric (MQ)	^(r) = Vi+w2
Inverse multiquadric (IMQ)	*)= /----г Vi+(^)
Inverse quadratic (IQ)	i
Gaussian (GS)

• -    расчет функции (1) для искомых точек пространства и выделение множества точек, для которых f (x) = const с учетом точности ε .

Недостатком такого прямого метода RBF является значительная вычислительная сложность, которая связана с необходимостью решать систему большой размерности, а также необходимостью сохранения больших объемов данных. Обобщенные характеристики временной и пространственной сложности данного алгоритма показаны в табл. 2.

Уменьшение сложности вычислений, описанное, например, в работе [9], достигается за счет уменьшения количества проекционных точек, то есть отбрасывания точек, которые не влияют на результат. Для отбрасывания используется итерационный „жадный” алгоритм [9]. В результате работы алгоритма формируется множество точек, при использовании которых, ошибка в определении поверхности не превышает заданный параметр точности ε .

В зависимости от выбранного параметра точности ε и набора входных данных, будет наблюдаться разная степень уменьшения сложности вычислений. В соответствии с экспериментальными данными [9], степень уменьшения лежит в пределах 0.14..0.92, при этом любая закономерность отсутствует.

Общее уменьшение времени определяется тем, что при работе „жадного” алгоритма и незначительном результирующем количестве проекционных точек на каждом шаге решается система маленькой размерности. Таким образом данный алгоритм не является универсальным, так как не обеспечивает гарантированного уменьшения вычислительных затрат для произвольных объектов.

Усовершенствованный метод, предложенный в [10] предполагает уменьшение числа операций за счет использования так называемых “компактных” RBF. Такие RBF – это функции, обладающие следующим свойством: функция меньше или равна 1 в окрестности исходной точки и больше 1 при удалении от нее.

Вычисление данной функции до решения системы значительно уменьшает ее размер за счет отбрасывания точек удаленных от заданной и в малой мере влияющих на результат. В зависимости от пространственного расположения заданных точек достигается различная степень снижения вычислительной сложности, а преобладание в матрице системы нулевых элементов позволяет сохранять ее в более компактной форме. На этапе построения матрицы и вычисления поверхности удобной и эффективной структурой для организации хранения данных является k-дерево [11], а результирующая матрица явля- ется сильно разреженной (см. рис. 1 справа) по сравнению с обычным методом RBF (см. рис. 2 слева), что позволяет использовать ускоренные методы решения систем, например [12].

Таким образом, средство сокращения вычислительных затрат при построении моделей методом компактной RBF – это применение эффективной древовидной структуры данных и использование методов ускоренного решения систем сразреженными матрицами.

Еще один известный метод – это метод быстрого вычисления множества потенциалов (FMM), который был адаптирован для решения данной задачи в работе [13]. Метод также позволяет значительно снизить временные и пространственные характеристики алгоритма за счет использования древовидных структур данных и аппроксимации модели с помощью, например, разложения в ряд Тейлора. Сущность метода быстрого вычисления состоит в следующем.

Пространство, в котором расположенные заданные точки, иерархически делится на элементарные подпространства. Такое распределение дает в результате дерево. Для любого подпространства на последнем уровне определяется два множества подпространств: приближенное и отдаленное. Приближенное содержит подпространства, которые расположены на том же уровне, что и искомое и имеют тот же родительский узел. Все другие подпространства составляют отдаленное множество. Процесс формирования модели поверхности с помощью функции вида (1) делится на два этапа: этап подготовки, который выполняется один раз, и этап вычисления, который повторяется для каждой искомой точки. На этапе вычисления часть функции (1), которая определяется точками из приближенных подпространств, вычисляется непосредственно, а часть, которая определяется точками в отдаленных подпространствах – с помощью аппроксимации. В зависимости от вида RBF, которая используется, применяются разные средства аппроксимации [13]. Однако данный метод не является универсальным, и выбор различных функций RBF требует различных подходов к аппроксимации.

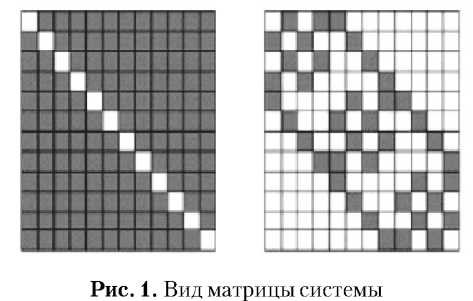
Таблица 2. Анализ соответствующих алгоритмов

Этап обработки	Алгоритм
	Обычный RBF	RBF с минимизацией	Компактный RBF	Быстрый RBF
Расчет RBF	О(п2)	О(и2)	О(п log и)	О(п2)
Решение системы	О^)	О(»2)	(Дп1 '^	О(п log»)
Расчет поверхности	О^тп)	О(тп)	О(т log»)	О(т + и logo)

Теоретические оценки рассмотренных методов, полученные в результате анализа соответствующих алгоритмов и экспериментальных исследований на наборах тестовых объектов [14], приведены в табл. 2.

Анализируя данные табл. 2, можно сделать следующие выводы:

• -    на этапе расчета матрицы значений функции RBF наименьшую

вычислительную сложность имеет метод компактной RBF;

• -    на этапе решения системы наименьшую вычислительную сложность имеет

метод быстрой RBF;

• -    на этапе расчета поверхности наименьшую вычислительную сложность

имеет метод компактной RBF.

Таким образом, если считать процесс рекон- струкции последовательным применением рассмотренных ранее этапов, то лучшие результаты с точки зрения минимального времени реконструкции при больших N должен показать метод компактной RBF. Поэтому целесообразно именно его использовать в составе программной системы для реконструкции моделей органов по результатам томографических исследований, структура которой предложена в [15].

ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ МЕТОДА КОМПАКТНОЙ RBF

Для осуществления трехмерного моделирования объектов предлагается следующая схема (см. рис. 2).

Предложенная схема предполагает слияние метода RBF и метода деформационного сопостав-

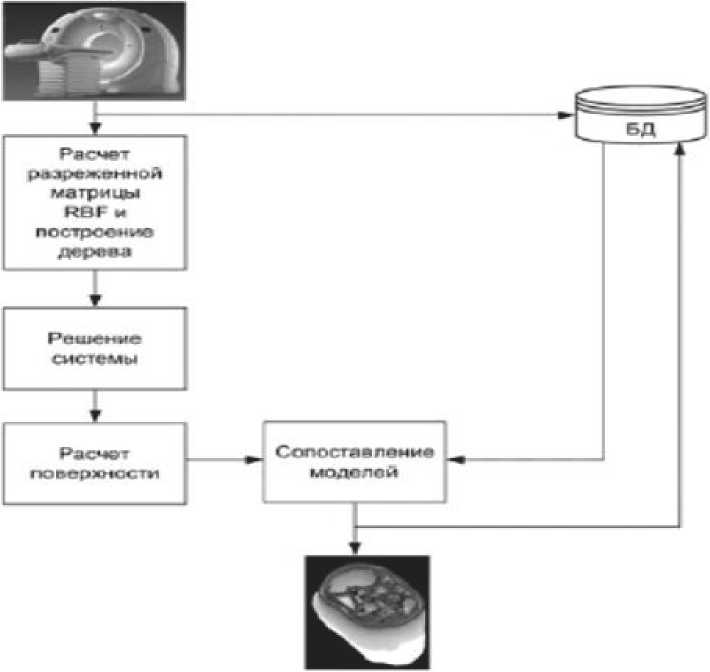
Рис. 2. Схема получения 3D-модели

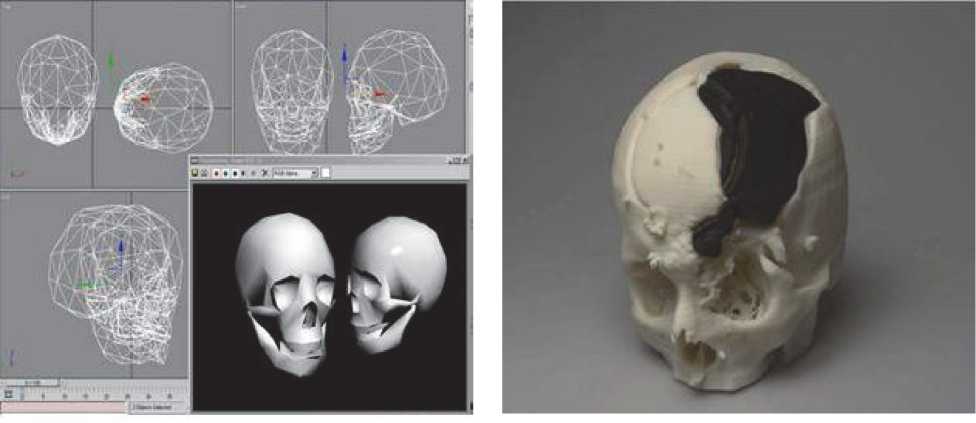
Рис. 3. Результаты моделирования

ления трехмерных моделей на основе исследований, изложенных в [16]. Примеры полученных с помощью предложенной схемы и компактного метода RBF моделей показаны на рис. 3 (череп).

В табл. 3 сведены численные результаты экспериментов по построению моделей объектов, представленных на рис. 3. При моделировании использовалась система следующей конфигурации: Intel Core 2 Duo 3.0 ГГц, 2Гб RAM.

В табл. 3 использованы следующие обозначения:

• t 1 – время расчета матрицы или построения дерева;

• t 2 – время решения системы;

• t 3 – время расчета поверхности.

ts – суммарное время построения модели.

Как видно из табл. 3, суммарное время построения модели при количестве точек, достигающем 10 ⁶ …10 ⁷ , достаточно приемлемое, т.е. использование метода компактной RBF в данном случае позволяет приблизиться к реальному времени и получить лучший результат по сравнению, например, с работой.

С помощью предложенной методики ведутся работы по созданию, не имеющего аналогов в мире, аппаратно-программного комплекса “Виртуальный хирург” для 3D моделирования операционного процесса и учебно-методических модулей для системного обучения врача-хирурга методикам открытой хирургии с небольшим размером операционного поля, методикам эндоваскулярной хирургии и эндоскопической хирургии на этапах додипломного и последипломного образования. Работы осуществляются при финансовой поддержке Министерства образования и науки Российской Федерации.

ВЫВОДЫ

В результате анализа временных и пространственных характеристик методов построения трехмерных моделей, основанных на использовании RBF и поверхностном представлении результата, выяснено, что при реконструкции моделей с большим числом точек (4N > 10 ) наибольший эффект, с точки зрения минимизации временных затрат, дает алгоритм „компактной RBF”. Данный алгоритм был реализован в составе программной системы для реконструкции трехмерных моделей органов. Результаты экспериментов подтверждают возможность использования метода компактной RBF при построении 3D-моделей объектов в реальном времени.

Ближайшей задачей для дальнейших исследований является исследование возможности адаптации метода построения 3D-моделей на

Таблица 3. Численные результаты экспериментов

Объект Brain Vertebra Кол-во точек Ю3 10 103 10° 10' 10" 104 HP 10° 10' 11, с 0.12 0.34 1.05 4.24 24.6 0.16 0.45 1.24 5.48 35.7 t2, с 0.20 0,97 3.65 12.3 67.2 0.31 1.07 5.06 14.6 76.5 13, с 0.15 0.45 1.34 4.96 26.5 0.18 0.51 2.04 6.12 30.4 ts, с 0.47 1.76 6,04 21.50 118.3 0.65 2.04 8.34 26.2 142.6 основе RBF к параллельной реализации, что теоретически позволит сократить временные затраты на моделирование сложных динамически изменяющихся во времени объектов.