Реабилитация модели атома Резерфорда

Показано что в планетарной модели атома Резерфорда существуют устойчивые по высоте - стационарные орбиты электрона, обоснована причина устойчивости и дискретность стационарных орбит.

Пишут [1], что « Планетарная модель атома Резерфорда соответствует современным представлениям о строении атома с уточнениями … Недостатком планетарной модели была невозможность объяснения ею устойчивости атомов. Так как электроны движутся …, то они по законам классической электродинамики должны излучать электромагнитные волны, теряя при этом на излучение кинетическую энергию орбитального движения и в результате «упасть» на ядро. Расчёты, выполненные с помощью методов классической электродинамики показывают, что электроны должны «упасть» на ядро за время порядка 10^-11 с.”

Эти уточнения, как известно, привели к созданию квантовой механики. Однако рассмотрим, насколько разрушительны процессы излучения для сохранения кинетической энергии электрона.

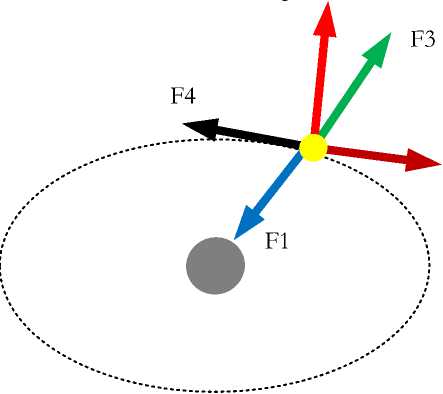
Рассмотрим электрон с массой т , который вращается вокруг собственной оси с угловой скоростью 661 и движется по некоторой траектории вокруг ядра с линейной скоростью V — см. рис. 1. На электрон действуют сила тяжести

F = тд , (1) где д - это ускорение свободного падения электрона на ядро; сила Кориолиса

Г₂ = —ZrntO t х v (2) и центробежная сила

F 3 = тш 2 К, (3) где R, 6 2 - мгновенные радиус и угловая скорость вращения в данной точке указанной траектории.

Omega

F2

Рис. 1.

Электрон из-за излучения теряет свою кинетическую энергию. Теряемая электроном мощность Р ₄ может быть определена как мощность некоторой силы F 4 сопротивления движению электрона, т.е.

Р 4 = F ₄ V. (4)

Пусть вектор 0)1 имеет три проекции — проекцию O ir на радиус, проекцию (Ою на касательную к окружности и проекцию 6 1Z на вертикаль. Рассмотрим еще проекцию W iro на плоскость окружности, проекцию 0 120 на вертикальную плоскость, касательную к окружности, и проекцию W 12 r на вертикальную плоскость, проходящую через радиус.

Движение тела будет устойчивым при выполнении трех условий:

Fi = -2т<°1до^

Г3 = -ZmcoizoV

F4 = —2m(°i2oV,(7)

где справа указаны проекции силы Кориолиса.

Из (4) с учетом (7) находим:

Р4 = -2ma)i2ov2.(8)

Формулы (1, 5) могут быть объединены. Тогда получим:

д = -2wiroV(9)

Формулы (3, 6) могут быть объединены. Тогда получим:

°2^R = ^- 2lzo v                          (10)

Из (8, 9, 10) находим:

(1™ =   2т^'                   (11)

( 1R0 =    2Ra) ,                               (12) 2KCU 2

O izo = -у                         (13)

В этих формулах неочевидной является формула (7). В ней указана сила сопротивления движению электрона, действующая вдоль скорости V, и проекция силы Кориолиса на эту же скорость. Такая проекция по определению (2) равна нулю. Объяснение приведено в приложении и основано на том, что реальная траектория электрона является спиральной линией. Там показано, что на некоторой «высоте» над ядром может существовать орбита электрона, сохраняющая свою высоту, обоснована устойчивость и дискретность таких стационарных орбит

Таким образом, если для электрона известны m, д, (2,R, то по (11, 12, 13) могут быть найдены проекции и сам вектор скорости (1. И наоборот, если известен вектор (1, то по (11, 12, 13) могут быть найдены скорость (2, радиус орбиты R и ускорение д. Последняя величина для определенного ядра определяет «высоту» орбиты. Следовательно, электрон с определенной скоростью ( имеет однозначно определенную орбиту.

Энергия вращения электрона вокруг собственной оси со скоростью ( 1 его момент импульса не изменяются. Энергия вращения электрона по окружности

W = G.5mv² = G.5m( 2 R² (14) не изменяется, поскольку не изменяется скорость ( 2 и радиус R орбиты. Сохранение этих величин происходит несмотря на то, что электрон постоянно теряет свою энергию, т.к. энергия электрона постоянно восстанавливается силой Кориолиса.

Такое действие силы Кориолиса возможно только в том случае, если она может совершать работу, т.е. эта сила является реальной силой. Математическое доказательство реальности этой силы дано в

[2, раздел 3]. Там показано, что сила Кориолиса может быть обоснована как следствие уравнений Максвелла, а источником энергии для этой силы является электрическое ядро.

Оппонент может сказать, что энергия ядра не бесконечна и, в конце концов, она будет растрачена на генерацию сил Кориолиса для всех электронов. Я с ним соглашусь - соглашусь с тем, что эти растраты вносят свой вклад в ядерный распад. Но это не повод для отказа от планетарной модели.

Модель атома Резерфорда должна быть возвращена в физику.

Приложение

В [3] показано, что электрон в вакууме движется по спиральной траектории, что является решением системы уравнений Максвелла [2]. В цилиндрических координатах г, ф, z функции тока имеют вид: к = q^ r cos( аф + %z) ,                      (1)

J ф = ЦУ ф sin( аф + xz)                    (2)

J z = qV z Sin( аф + xz),                        (3)

где q - заряд электрона, a, X — некоторые константы, V _T , V , , V _z -константы - скорости движения электрона по координатам. При этом г = const . На рис. 2 показаны три винтовые линии, описываемые функциями (10, 11) тока с проекциями J , и /_z . На рис. 1 для примера показаны: толстая линия при a = 2, х = 0.8 , средняя линия при a = 0.5,х = 2 и тонкая линия при a = 2, X = 1.6 .

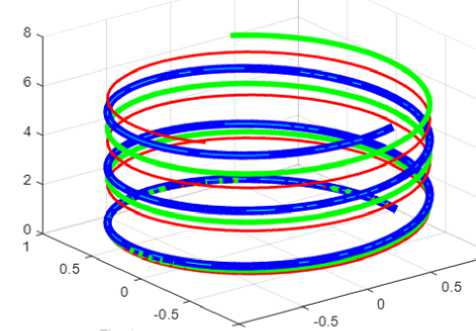
Рис. 2

Далее мы будем рассматривать функции покоординатных скоростей

Vr = ^ = PrCOS( p),(4)

в параметрической форме с параметром p = dip + xz.(5)

Таким образом, электрон движется со скоростью

V = [Vr, Vp, Vz],(6)

причем

Vr = vrcos( p),(7)

Vp = VpSin( p),(8)

Vz = VzSin( p).(9)

Перейдем к декартовым координатам и далее будем рассматривать вектор

V = [V,, Vy, Vz],(10)

где

• V, = Vrcos( p) -VpSin( p),(11)

Vy = Vrsin( p) + Vpcos( p).(12)

или, с учетом (8, 9),

• V, = vr cos(p) cos(p) - vp sin(p) sin(p),(13)

Vy = vr cos(p)sin(p) + vpsin(p) cos(p).(14)

Важно для дальнейшего отметить, что функции (13, 14) являются периодическими функциями от координаты z, что следует из (5).

Если электрон вращается вокруг собственной оси с угловой скоростью (, то на него действует сила Кориолиса F = —2m

где т - масса электрона. При этом

F_c = [F,, Fy, Fz],

^{(   [(}х, ⁽у, ⁽Z_ .

Из (10-12) найдем:

Г ^F, = (O_y^Vz^—z^Vy ] F_c = I ^Fy = z^Vx ^—^x^Vz I.

[ ^Fz = ^x^Vy ^—^y^Vx]

Видно, что сила Кориолиса имеет проекцию F_Z на ось z, т.е. на траекторию движения электрона. Сила F_Z определяется через функции (13, 14) и поэтому является периодической.

Предположим, что электрон вращается вокруг ядра и обозначим длину траектории электрона на одном замкнутом витке как L. Рассмотрим среднее значение силы F_z на длине L.u обозначим его как F_zmid. В силу периодичности силы F_z величина F_zmi^ может принимать различные по знаку значения.

Вместе с этой силой на электрон действует сила F4 сопротивления движению электрона, которая пропорциональна длине L. Рассмотрим суммарную силу, действующую на электрон вдоль траектории:

Ftrek = Fzmid-F4L.                       (19)

При этом

• 1.    если F_tre< = 0, то длина траектории не меняется.

• 2.    если Ft_re< > 0, то электрон ускоряется, постепенно удаляется и его траектория удлиняется,

• 3.    если Ft_re< < 0, то электрон замедляется, постепенно падает на ядро и его траектория укорачивается.

dFlfg^

Можно рассмотреть еще производную в точке с таким значением L, где Ftre< = 0. При "~~ < 0 траектория является устойчивой. Действительно, при уменьшении высоты длина L уменьшается, но при этом увеличивается Ftre< и электрон ускоряется, а при этом он поднимается.

Таким образом, существуют устойчивые по высоте траектории – стационарные орбиты. Эти орбиты расположены по высоте дискретно. Устойчивость стационарных обеспечивается силой Кориолиса, действующей на излучающий электрон.