Реакционная способность как один из критериев выбора сырья для получения активных тонкодисперсных минеральных порошков
Автор: Морозова Марина Владимировна
Журнал: Нанотехнологии в строительстве: научный интернет-журнал @nanobuild
Рубрика: Технологии производства строительных материалов и изделий
Статья в выпуске: 3 т.15, 2023 года.
Бесплатный доступ
Введение. Наиболее простым и распространенным способом получения тонкодисперсных минеральных порошков является механическое диспергирование. В процессе измельчения материала затрачивается определенная работа (энергия), которая расходуется на образование новой поверхности. Поэтому не всегда понятно, действительно ли разрушение кристаллической решетки твердого тела приводит к активации получаемого раздробленного материала. Так, ключевыми характеристиками тонкодисперсных минеральных порошков, по которым можно судить об активационных процессах, являются величина удельной поверхности (Ssp) и удельная свободная поверхностная энергия, числено равная поверхностному натяжению (о) твердого тела. Поэтому для оценки процесса механической активации сырья был предложен ряд моделей, основанных на определении данных характеристик. Так, одним из самых корректных способов, на наш взгляд, является способ, основанный на энергетическом подходе к оценке механоактивационных процессов. В данной модели заложено определение относительного изменения свободной поверхностной энергии (ΔES/ES0) материала при получении дисперсной системы. В то же время выбор наиболее эффективного сырья для получения композиционных вяжущих может осуществляться на основе критерия активности поверхности (ks), который используется как критерий, характеризующий реакционную способность тонкодисперсных минеральных порошков после их механической дезинтеграции. Поэтому целью данной работы стал расчет относительного изменения поверхностной энергии тонкодисперсных минеральных порошков различной сырьевой природы и выявление возможной функциональной взаимосвязи между параметром ΔES/ES0 и величиной активности поверхности для исследуемых систем горных пород. Методы и материалы. В качестве материалов для проведения исследований были выбраны осадочные горные породы Архангельской области: полиминеральный песок и сапонитсодержащий материал (представитель бентонитовых глин). Перед началом экспериментов образцы горных пород доводили до постоянной массы при температуре 105оС. Химический состав образцов определяли на рентгенофлуоресцентном анализаторе «МетЭксперт». Высокодисперсные фракции горных пород получали методом сухого помола на планетарной шаровой мельнице Retsch PM100. Определение размерных характеристик проводили на анализаторе размера субмикронных частиц «DelsaNano» методом фотонно-корреляционной спектроскопии. Удельная поверхность определялась методом газопроницаемости на приборе «ПСХ-10». Для расчета поверхностного натяжения измеряли краевой угол на установке «Easy Drop». Поверхностное натяжение для высокодисперсных проб рассчитывали методом ОВРК. Результаты и обсуждение. Рассчитанные макроэнергетические характеристики исследуемых образцов показали, что энергия атомизации для полиминерального песка составила 1910,72 кДж/моль, а для сапонитсодержащего материала 1826,94 кДж/моль. При этом массовая удельная энергия атомизации для песка и ССМ равны 30,41•103 кДж/кг и 26,94•103 кДж/кг, соответственно. В процессе диспергирования было получено несколько фракций высокодисперсных порошков горных пород, которые охарактеризовали средним размером частиц и удельной поверхностью. Рассчитанное методом ОВРК поверхностное натяжение (и его составляющие) показало, что для всех исследуемых проб поляризационный эффект (σSP) преобладает над дисперсионным взаимодействием (σSD). При этом по мере возрастания Ssp численное значение отношения σSP/σSD увеличивается. Это свидетельствует об увеличении количества активных центров поверхности, связанных с перераспределением энергетического потенциала системы. Рассчитанные величины свободной поверхностной энергии (ES), активности поверхности (ks) и относительное изменение свободной поверхностной энергии показали, что ks и ΔES/ES0 возрастают по мере увеличения продолжительности диспергирования порошков. Полученные функциональные зависимости ks = f(ΔES/ES0) для исследуемых образцов полиминерального песка и сапонитсодержащего материала имеют линейный характер и подчиняются уравнению общего вида у = a•x + b. При этом коэффициент «a» характеризует динамику изменения реакционной способности материала при увеличении продолжительности механического размола, а параметр «Ь» его реакционную активность в макросостоянии. Сравнение коэффициентов «a» исследуемых дисперсных систем показало, что в отличие от полиминерального песка реакционная способность сапонитсодержащего материала возрастает в 1,5 раза бы стрее, по мере увеличения продолжительности помола. Полученная функциональная взаимосвязь между используемыми критериями оценки процесса механоактивации минерального сырья различной природы показывает корректность применяемых моделей. Заключение. Рассчитанные макроэнергетические характеристики образцов горных пород показали, что энергия атомизации для полиминерального песка и сапонитсодержащего материала имеет близкие значения.
Полиминеральный песок, сапонитсодержащий материал, активность поверхности, дисперсность, энергия атомизации, поверхностное натяжение
Короткий адрес: https://sciup.org/142238067
IDR: 142238067 | УДК: 691.223.7 | DOI: 10.15828/2075-8545-2023-15-3-238-245
Текст научной статьи Реакционная способность как один из критериев выбора сырья для получения активных тонкодисперсных минеральных порошков
В настоящее время поиск и изучение альтернативных сырьевых материалов, пригодных для получения тонкодисперсных минеральных порошков, является важной научно-практической задачей, решение которой позволит более широко внедрять ресурсосберегающие технологии при получении композитов строительного назначения. В настоящее время область применения минеральных порошков в индустрии строительных материалов весьма обширна: минеральные порошки используются в качестве пуццолановых добавок [1–3], наполнителей для бетонных и грунтобетонных смесей [4, 5], сырьевых смесей для получения изделий сухим или мокрым прессованием [6, 7].
Наиболее простым и распространенным способом получения тонкодисперсных минеральных порошков является механическое диспергирование. Это связано с тем, что при механическом помоле твердого тела образуется поверхность, идентичная по своей природе первоначальной [8].
Известно, что в процессе механического диспергирования затрачивается определенная работа (энергия), которая в дальнейшем расходуется на упругую и пластическую деформацию, выделившуюся теплоту и на образование новой поверхности. При этом в твердых телах возможны процессы, при которых формирование новой поверхности может затрагивать и объемную фазу. Поэтому всегда стоит вопрос о том, действительно ли разрушение кристаллической решетки твердого тела приводит к активации получаемого раздробленного материала.
Так, в работах [9–11] показано, что ключевыми характеристиками тонкодисперсных минеральных порошков, по которым можно судить об актива- ционных процессах, являются величина удельной поверхности (Ssp), характеризующая степень дисперсности материала, и удельная свободная поверхностная энергия, числено равная поверхностному натяжению (σ) твердого тела. Поэтому для оценки процесса механической активации сырья был предложен ряд моделей, основанных на определении данных характеристик.
Так, авторами [12] разработана математическая модель, в основе которой лежит определение величины и знака изменения изобарно-изотермического потенциала поверхности ∆GS (энергии Гиббса), сопровождающее процесс измельчения минерального сырья. Данный параметр, по мнению авторов, является критерием возможности протекания самопроизвольных трансформационных процессов, происходящих при механическом диспергировании материалов [13–14].
Продолжая исследования в этом направлении, авторы работ [15, 16] считают, что для тонкодисперсных порошков важнейшей характеристикой является энергетическое состояние системы, оцениваемое по величине свободной поверхностной энергии (ES). Основываясь на классических представлениях коллоидной химии, данную величину можно рассчитывать как произведение поверхностного натяжения и удельной поверхности анализируемого объекта [17, 18].
Дальнейшее развитие этого направления позволило предложить, на наш взгляд, новую, более совершенную модель оценки степени активации материала при его диспергировании. В основе такого подхода заложено определение относительного изменения свободной поверхностной энергии материала при получении дисперсной системы [19–21]. Математическим описанием данного подхода является
ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ выражение (1), объединяющее экспериментально определяемые величины поверхностного натяжения системы и ее удельную поверхность:
др / S' \
— = (1-6(7)- -1, (1)
^-sO \^spO/ где «0» – индекс, обозначающий начальное состояние системы; δ – относительное изменение величины поверхностного натяжения, определяемое по формуле:
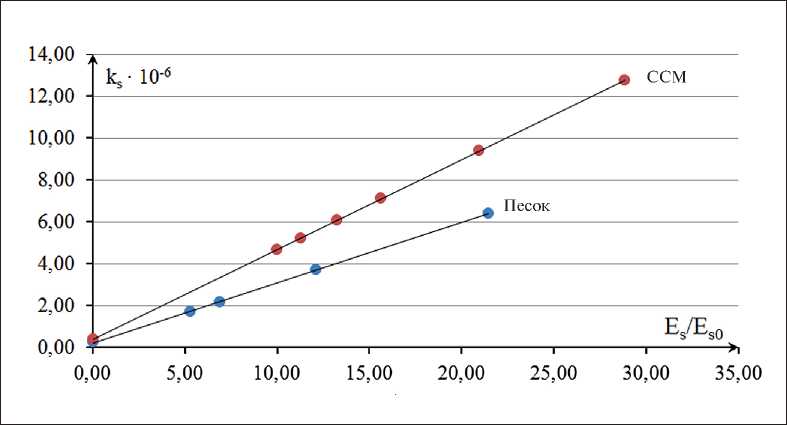
Д(Т , (2) ffo ^o где σ0 – начальное поверхностное натяжение системы; σi – поверхностное натяжение системы после процесса диспергирования; ∆ES/ES0 – относительное изменение свободной поверхностной энергии. В то же время в работах [22–24] выбор наиболее эффективного сырья для получения композиционных вяжущих осуществляется на основе критерия активности поверхности (ks), который показывает долю общего потенциального энергетического запаса анализируемой горной породы, полученной в результате ее генезиса, перешедшую в поверхностную в процессе механической активации сырья. Расчет параметра ks осуществляется исходя из химического состава материала, удельной поверхности системы и свободной поверхностной энергии единицы площади поверхности (σ). Параметр активности поверхности базируется на макроэнергетических показателях анализируемого сырья: энергии атомизации (EA, кДж/моль) и ее удельных величинах – объемной удельной энергии атомизации (энергоплотность – EV, кДж/см3) или массовой удельной энергии атомизации (Em, кДж/г) [15]. Поэтому величина ks может быть также использована как критерий, характеризующий реакционную способность тонкодисперсных минеральных порошков после их механической дезинтеграции. В [20] для ряда осадочных горных пород определена величина ks. На основании вышеизложенного целью данной работы стал расчет относительного изменения поверхностной энергии тонкодисперсных минеральных порошков различной сырьевой природы по выражению (1); выявление возможной функциональной взаимосвязи между параметром ∆ES/ES0 и величиной активности поверхности для исследуемых систем горных пород. МЕТОДЫ И МАТЕРИАЛЫ В качестве материалов для проведения исследований были выбраны две горные породы Архангель- ской области [23]. Это карьерный песок месторождения «Кеницы». В качестве другого объекта исследований использован сапонитсодержащий материал (представитель бентонитовых глин), выделенный путем электролитного осаждения из суспензии оборотной воды процесса обогащения кимберлитовых руд месторождения алмазов имени М.В. Ломоносова [21]. Перед началом экспериментов образцы горных пород доводили до постоянной массы при температуре 105оС. Модуль крупности и истинную плотность песка определяли по ГОСТ 8735-88. Истинную плотность для глины (сапонитсодержащий материал – ССМ) определяли по ГОСТ 21216-2014. Химический состав образцов определяли на рентгенофлуоресцентном анализаторе «МетЭксперт». Высокодисперсные фракции горных пород получали методом сухого помола на планетарной шаровой мельнице Retsch PM100. Для каждой исследуемой пробы опытным путем были подобраны оптимальные режимные параметры диспергирования, позволяющие получать высокую воспроизводимость результатов по размерным характеристикам частиц (не менее трех параллельных испытаний). Скорость вращения ротора мельницы составляла 420 об/мин. Для диспергирования использовали карбидвольфрамовые размольные тела шарообразной формы в количестве 20 шт и размольный стакан из того же материала. Определение размерных характеристик проводили на анализаторе размера субмикронных частиц Delsa Nano Series Zeta Potential and Submicron Particle Size Analyzers («DelsaNano») методом фотоннокорреляционной спектроскопии, основанным на принципе динамического рассеяния света. Удельная поверхность высокодисперсных систем горных пород определялась методом газопроницаемости на приборе «ПСХ-10». Для расчета поверхностного натяжения измеряли краевой угол на установке «Easy Drop» при температуре окружающей среды 25±1оС. Исследование выполняли на образцах-таблетках, изготовленных путем запрессовки размолотого песка и сапонитсо-держащего материала на прессе «ПЛГ-20» (нагрузка 20 кПа) в металлическую форму диаметром 20 мм. Поверхностное натяжение для высокодисперсных проб рассчитывали методом ОВРК (Оуэнса – Вендта – Рабеля – Каелбле), основанным на измерении равновесного угла смачивания (θ) жидкостями (дистиллированной воды, декана, глицерина и этиленгликоля) с известными значениями поверхностного натяжения и его дисперсионной (σLD) и поляризационной (σLP) составляющими. При этом полученные функциональные зависимости метода ОВРК: ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ описываются линейными уравнениями, где θ – угол смачивания исследуемого материала, σL, σLD, и σLP – суммарное, дисперсионное и поляризационное поверхностные натяжения рабочих жидкостей (соответственно). Угловой коэффициент данной линейной зависимости равен поляризационной части поверхностного натяжения образца, а экстраполяция данной прямой на ось ординат позволяет рассчитать дисперсионную составляющую. Поверхностное натяжение анализируемых образцов вычисляется по следующему выражению: σS = σSP + σSD, где σSP и σSD – полярная и дисперсионная составляющие поверхностного натяжения исследуемого материала, Дж/м2. Расчет относительного изменения поверхностной энергии осуществляли по выражению (1). Величину поверхностной энергии вычисляли как произведение удельной поверхности анализируемого порошка на его поверхностное натяжение. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ Результаты по определению грансостава исследуемой пробы песка месторождения «Кеницы» показали, что его можно классифицировать как песок средней крупности (модуль крупности 2,21). Полученные значения истинных плотностей (ρист) исследуемых горных пород показали близкие по значениям результаты: 2640 кг/м3 и 2630 кг/м3 для полиминераль-ного песка и сапонитсодержащего материала (ССМ), соответственно. Исходными данными для расчета энергии атомизации горных пород являются минеральный состав исследуемых образцов в пересчете на оксиды, а также энтальпии образования соответствующих оксидов, значения которых приведены в справочной литературе [25]. С учетом молекулярных масс оксидных соединений была рассчитана удельная массовая энергия атомизации опытных образцов. Элементные составы (в пересчете на оксиды), а также стандартные энтальпии образования данных оксидов и их молекулярные массы представлены в табл. 1. С использованием представленных в табл. 1 данных рассчитаны значения ЕА и Em исследуемых образцов. Так, энергия атомизации для полимине-рального песка составила 1910,72 кДж/моль, а для сапонитсодержащего материала – 1826,94 кДж/ моль. При этом массовая удельная энергия атомизации для песка и ССМ равны 30,41•103 кДж/кг и 26,94•103 кДж/кг, соответственно. В продолжение исследований путем механического диспергирования было получено несколько фракций высокодисперсных порошков горных пород, которые охарактеризовали средним размером частиц и удельной поверхностью (табл. 2). Полученные значения среднего размера частиц показали, что при одинаковых режимных параметрах помола процесс диспергирования ССМ требует больших затрат энергии, нежели песка. Так, при продолжительности помола 30 минут частицы песка имеют средний диаметр 329 нм, в то время как у ССМ этот параметр достигает значения 664 нм. Однако сравнение величин удельной поверхности материалов при времени диспергирования 30 минут имеют близкие значения: песок 2860 м2/кг, ССМ – 2821 м2/кг. В табл. 3 приведены экспериментальные данные измерения углов смачивания (θ) и косинусов этих углов для опытных образцов эталонными жидкостями, полученные для реализации метода ОВРК. Представленные данные (табл. 3) позволили рассчитать по функциональным зависимостям (выраже- Таблица 1 Состав исследуемых образцов в пересчете на оксиды, энтальпии образования оксидов (∆Н) и их молекулярная масса (М) Оксид Содержание, % ∆H298•10–3, кДж/кмоль Молекулярная масса оксида, кг/кмоль песок ССМ SiO2 90,56 51,83 –910,94 60,09 Al2O3 5,77 10,07 –1675,70 100,18 MgO 0,48 19,7 –601,50 40,31 Fe2O3 0,88 10,54 –822,00 159,70 CaO 0,25 4,79 –635,10 56,08 K2O 0,28 1,77 –362,00 94,20 SO3 0,07 0,46 –439,00 80,06 P2O5 0,06 0,76 –1507,20 141,94 Na2O 1,65 0,08 –414,84 61,98 ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ Таблица 2 Характеристика высокодисперсных фракций песка и сапонитсодержащего материала Продолжительность помола (τ), мин Средний размер частиц, d, нм Удельная поверхность, Ssp, м2/кг песок ССМ песок ССМ –* 1350 1 17 5 672 1113 781 1861 10 559 828 992 2081 20 406 764 1667 2416 30 329 664 2860 2821 60 — 519 — 3728 90 — 445 — 5067 * параметр не определялся Таблица 3 Краевые углы смачивания для опытных образцов с разной продолжительностью (τ) помола Представленные данные (табл. 4) показывают, что для всех исследуемых проб поляризационный эффект преобладает над дисперсионным взаимодействием. По мере возрастания удельной поверхности численное значение отношения σSP/σSD увеличивается. Данный факт может свидетельствовать об увеличении количества активных центров поверхности, что связано с перераспределением ее энергетического потенциала, так как для всех тонкодисперсных минеральных порошков наблюдаются практически одинаковые значения суммарного поверхностного натяжения (65,68 … 68,00)•10–3 Дж/м2. В продолжение исследований для тонкодисперсных фракций минеральных порошков были рассчитаны величины свободной поверхностной энергии (ЕS), активности поверхности (ks) и относительное изменение свободной поверхностной энергии (∆ES/ES0) (табл. 5). Энергетические характеристики порошков (табл. 5) показали, что активность поверхности и относительное изменение поверхностной энергии системы возрастают по мере увеличения продолжительности диспергирования минеральных компонентов. Для выявления возможной взаимосвязи между значениями величины активности поверхности (ks) горных пород и относительного изменения свобод- ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ Таблица 4 Значения поверхностного натяжения порошков горных пород в зависимости от продолжительности (τ) помола Образец τ, мин Коэф. линейного уравнения σSP, мДж/м2 σSD, мДж/м2 σk•103, Дж/м2 a b Песок 0 6,82 4,38 46,52 19,16 65,68 5 6,87 4,39 47,18 19,25 66,43 10 6,93 4,36 48,05 19,01 67,06 20 6,99 4,35 48,85 18,97 67,81 30 7,03 4,32 49,35 18,66 68,00 ССМ 0 6,97 4,34 48,65 18,85 67,50 5 6,98 4,35 48,70 18,93 67,62 10 6,98 4,36 48,77 18,98 67,75 20 7,00 4,34 49,01 18,81 67,82 30 7,01 4,32 49,20 18,68 67,88 60 7,01 4,32 49,20 18,69 67,89 90 7,02 4,32 49,22 18,70 67,92 Таблица 5 Энергетические характеристики порошков Полученные функциональные зависимости ks = f(∆ES/ES0) для исследуемых образцов полиминераль-ного песка и сапонитсодержащего материала имеют линейный характер. Математическим выражением данных зависимостей являются уравнения (4) и (5): – для песка AES7 ks = (2,87 ■ —- + 2,27) ■ 10"7 ;(4) bso – для ССМ ДЕ57 ks = (4,29 ■ —- + 4,07) ■ 10"7 .(5) Eso При этом коэффициент «a», по нашему мнению, характеризует динамику изменения реакционной способности материала при изменении продолжительности механического размола, а параметр «b» – его реакционную активность в макросостоянии (до начала процесса механоактивации). Данные, получаемые по уравнениям (4) и (5), хорошо согласуются с экспериментальными результатами, представленными в табл. 2. ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ Рис. Зависимость относительного изменения свободной поверхностной энергии от активности поверхности тонкодисперсных минеральных порошков горных пород Сравнение коэффициентов «a» исследуемых дисперсных систем показало, что в отличие от по-лиминерального песка реакционная способность сапонитсодержащего материала возрастает в 1,5 раза быстрее в единицу времени по мере увеличения продолжительности помола. Таким образом, можно утверждать, что полученная функциональная взаимосвязь между используемыми критериями оценки процесса механоактивации минерального сырья различной природы показывает корректность применяемых моделей. ЗАКЛЮЧЕНИЕ Рассчитанные макроэнергетические характеристики образцов горных пород с использованием результатов рентгенофлюоресцентного анализа показали, что энергия атомизации для полиминерального песка составила 1910,72 кДж/моль, а для сапонитсо-держащего материала – 1826,94 кДж/моль. При этом массовая удельная энергия атомизации для песка и ССМ равна 30,41•103 кДж/кг и 26,94•103 кДж/кг, соответственно. В качестве математических моделей оценки эффективности процесса механоактивации минерального сырья можно использовать относительное изменение свободной поверхностной энергии, связанное с изменениями поверхностного натяжения порошков и удельной поверхности в процессе размола сырья, или активность поверхности, определяющую перераспределение потенциальной энергии системы в макросостоянии и после процесса механического диспергирования. Установлена функциональная взаимосвязь между данными критериями, которая характеризуется прямолинейной зависимостью.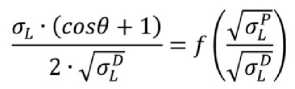
Образец
τ, мин
Краевые углы смачивания, θср ±0,1
декан
этиленгликоль
глицерин
вода
θ
cos θ
θ
cos θ
θ
cos θ
θ
cos θ
Песок
0
8,76
0,988
13,45
0,973
16,37
0,959
15,55
0,963
5
5,36
0,996
11,88
0,979
13,65
0,972
12,98
0,974
10
4,10
0,997
12,80
0,975
14,12
0,970
8,30
0,990
20
8,13
0,990
9,48
0,986
10,64
0,983
3,98
0,998
30
14,66
0,967
7,99
0,990
9,70
0,986
4,30
0,997
ССМ
0
10,09
0,985
7,16
0,992
15,34
0,964
4,09
0,997
5
7,45
0,992
9,64
0,986
13,45
0,973
3,45
0,998
10
6,98
0,993
9,05
0,988
12,37
0,977
2,64
0,999
20
7,05
0,992
13,58
0,972
10,32
0,984
1,87
0,999
30
9,89
0,985
14,00
0,970
9,77
0,985
2,09
0,999
60
10,11
0,984
13,89
0,971
9,16
0,987
2,87
0,999
90
9,76
0,986
13,93
0,971
9,02
0,988
2,17
0,999
ние 3) поверхностное натяжение (и его составляющие) для исследуемых порошковых систем горных пород. Эти зависимости (выражение 3) хорошо описываются линейными уравнениями вида y = a•x + b с высоким значением коэффициента достоверности аппроксимации (R2 = 0,98). Значения коэффициентов этих уравнений и рассчитанное поверхностное натяжение анализируемых порошков горных пород представлены в табл. 4.
Образец
τ, мин
Свободная поверхностная энергия, ЕS, Дж/кг
Активность поверхности k•106
δσ
Ssp/Ssp0
∆Es/Es0
Песок
0
8,08
0,27
–
1,00
0,00
5
51,94
1,71
0,011
6,36
5,28
10
66,52
2,19
0,021
8,07
6,90
20
113,04
3,72
0,032
13,55
12,11
30
194,50
6,40
0,035
23,25
21,43
ССМ
0
11,40
0,42
–
1,00
0,00
5
125,84
4,67
0,002
11,02
10,00
10
140,99
5,23
0,004
12,32
11,28
20
163,83
6,08
0,005
14,30
13,23
30
191,49
7,11
0,006
16,70
15,61
60
253,09
9,39
0,006
22,07
20,94
90
344,05
12,77
0,006
30,00
28,82
ной поверхностной энергии системы (∆ES/ES0) были построены функциональные зависимости вида ks = f(∆ES/ES0) (рис.).
Список литературы Реакционная способность как один из критериев выбора сырья для получения активных тонкодисперсных минеральных порошков
- Соскин М.И., Шулепова А.В., Шаманов В.А. Гипсоцементно-пуццолановое вяжущее с наноструктурными добавками // Успехи современной науки и образования. 2016. Т. 5, № 12. 155–159.
- Санчес де Рохас М.И., Асенсио Е., Фриас М., Куэвас И., Медина К. Низкоклинкерные цементы, содержащие строительные отходы и лом как пуццолановую добавку // Цемент и его применение. 2020. № 2. 84–89.
- Абдуллаева М.Я., Шихалиев К.С. Исследование влияния минерального наполнителя на свойства дорожно-строительного битума // Theoretical & Applied Science. 2016. № 4 (36). 106–110.
- Шошин Е.А. Перспективы применения тонкомолотых минеральных наполнителей в производстве высокопрочных цементных бетонов // Техническое регулирование в транспортном строительстве. 2019. № 6 (39). 338–342.
- Жугинисов М.Т., Кушеков Е.К. Жаростойкий бетон с применением кварцевого песка // Материаловедение. 2017. № 3 (23). 4–18.
- Якимович Г.Д. Получение мелкоштучных изделий методом сухого формования // Проблемы современного бетона и железобетона. 2017. № 9. 515–530.
- Багдасаров А.С., Урусов Д.А. Технологическая линия полусухого прессования производства фосфогипсовых стеновых изделий // Строительные материалы. 2013. № 5. 80–81.
- Потапова Е.Н., Манушина А.С., Зырянов М.С., Урбанов А.В. Методы определения пуццолановой активности минеральных добавок // Строительные материалы, оборудование, технологии XXI века. 2017. № 7-8 (222-223). 29–33.
- Нелюбова В.В., Строкова В.В., Данилов В.Е., Айзенштадт А. М. Комплексная оценка активности кремнеземсодержащего сырья как показателя эффективности механоактивации // Обогащение руд. 2022. № 2. 18–26. https://doi.org/10.17580/or.03.02.2022
- Алфимова Н.И., Калатози В.В., Карацупа С.В., Вишневская Я.Ю., Шейченко М.С. Механоактивация как способ повышения эффективности использования сырья различного генезиса в строительном материаловедении // Вестник Белгородского государственного технологического университета им. В.Г. Шухова. 2016. № 6. 85–89.
- Голик В.И., Титова А.В. Комбинированные технологии активации минерального сырья // Горная промышленность. 2021. № 5. 100–105.
- Фролова М.А., Тутыгин А.С., Айзенштадт А.М., Махова Т.А., Поспелова Т.А. Применение термодинамического подхода к оценке энергетического состояния поверхности дисперсных материалов // Нанотехнологии в строительстве. 2011. Т. 3, № 6. 13–25.
- Айзенштадт А.М., Махова Т.А., Фролова М.А., Тутыгин А.С., Стенин А.А., Попова М.А. Проектирование состава нано- и микроструктурированных строительных композиционных материалов // Промышленное и гражданское строительство. 2012. № 10. 14–18.
- Lesovik V., Ayzenshtadt A., Lesovik R., Frolova M., Strokova V. “Green” composites for north-arctic region development. Open Ecology Journal. 2014; 7(1): 32–36.
- Лесовик В.С., Фролова М.А., Айзенштадт А.М. Поверхностная активность горных пород // Строительные материалы. 2013. № 11. 71–74.
- Абрамовская И.Р., Айзенштадт А.М., Фролова М.А., Вешнякова Л.А., Тутыгин А.С. Энергетика высокодисперсных композитов горных пород // Нанотехнологии в строительстве. 2013. Т. 5, № 3. 56–65.
- Вешнякова Л.А., Дроздюк Т.А., Айзенштадт А.М., Фролова М.А., Тутыгин А.С. Поверхностная активность кремнесодержащих горных пород // Материаловедение. 2016. № 5. 45–48.
- Данилов В.Е., Королев Е.В., Айзенштадт А.М., Строкова В.В. Особенности расчета свободной энергии поверхности на основе модели межфазного взаимодействия Оунса–Вендта–Рабеля–Кьельбле // Строительные материалы. 2019. № 11. 66–72. https://doi.org/10.31659/0585-430X-2019-776-11-66-72
- Королев Е.В., Гришина А.Н., Пустовгар А.П. Поверхностное натяжение в структурообразовании материалов. Значение, расчет и применение // Строительные материалы. 2017. № 1-2. 104–108
- Данилов В.Е., Айзенштадт А.М., Фролова М.А., Тутыгин А.С. Изменение поверхностной энергии – критерий оптимизации состава бесцементного композиционного вяжущего // Материаловедение. 2018. № 2. 39–43.
- Малыгина М.А., Айзенштадт А.М. , Е. В. Королев, Т. А. Дроздюк, М. А. Фролова. Аспекты электролитной коагуляции сапонитсодержащей суспензии оборотной воды горноперерабатывающих предприятий // Экология и промышленность России. 2022. Т. 26, № 11. С. 27–33. https://doi.org/10.18412/1816-0395-2022-11-27-33
- Айзенштадт А.М., Королев Е.В., Дроздюк Т.А., Данилов В.Е., Фролова М.А. Возможный подход к оценке дисперсионного взаимодействия в порошковых системах // Физика и химия обработки материалов. 2021. № 3. 40–48. https://doi.org/10.30791/0015-3214-2021-3-40-48
- Морозова М.В., Айзенштадт А.М., Акулова М.В., Фролова М.А. Фазово-структурная гетерогенность и активность поверхности порошков полиминеральных песков // Нанотехнологии в строительстве. 2022. Т. 14, № 2. 89–95. https://doi.org/10.15828/2075-8545-2022-14-2-89-95
- Шаманина А.В., Кононова В.М., Данилов В.Е., Фролова М.А., Айзенштадт А.М. Аспекты определения активности поверхности дисперсных систем на основе минеральных порошков // Материаловедение. 2021. № 7. 30–36.
- Gurvich L.V., Veits I.V., Medvedev V.A. and etc. Thermodynamic properties of individual substances: a reference book. Volume IV. Moscow: Nauka; 1982.


