Реактивная гидравлическая турбина с соплом на основе колеса Сегнера

Количественные показатели всех видов возобновляемых источников электроэнергии (ветровая, солнечная и гидроэнергетика) велики, а доля используемого энергетического потенциала составляет около 26 %. Так, доля ветровой энергетики в 2012 году с гидроэнергетикой составила 26 % при всей доле 39 %. При этом рост мощности составил 3 %, и мощность достигнута 990 ГВт, мощность других видов увеличилась на 21,5 % (480 гВт) [1]. Обеспечение электроэнергией и модернизация существующих централизованных систем (газопроводов и электросетей) для регионов с объектами малой плотности энергонагрузок зачастую экономически не выгодны и не везде возможны из-за дефицита электрогенерирующих мощностей.

В работе [2–4] рассматриваются вопросы, связанные с технико-экономическими характеристиками, параметрами для аккумулирующих станций микроГЭС. Особенно хорошо и просто объясняются вопросы касательно аккумуляции и распределения собранной электроэнергии, а в [5] – создание микросетей (для отдельных потребителей) и рациональное использование собранной электроэнергии.

Проводились численные исследования по изучению параметров спиральной сферической турбины диаметром 1,4 м [6]. Здесь основное внимание уделено вопросу использования возду- ховодов круглого и прямоугольного сечения. Было показано, что у прямоугольного воздуховода коэффициент мощности турбины выше на 4,7 % по сравнению с круглым. Аналогично с турбиной Горлова и Дарье (сферической формы) диаметром 1 м и 1,14 м [7]. Показано, что турбина Горлова имеет более высокий КПД (28 %) по сравнению с турбиной Дарье (21 %). В случае со сферическими турбинами с диаметром менее 1 м были проведены исследования компанией Oladosu [8]. Численные расчеты показали, что турбина с диаметром 233,6 мм имеет максимальную мощность 1080 и 2663 W при случае из нержавеющей стали и алюминия соответственно. Максимальная потеря напора составила 9,7 %. Таким же образом проанализировали при помощи вычислений новую сферическую турбину диаметром 894,08 мм. Здесь КПД достиг 22 % при передаточном числе скорости 2,4 и зазоре 12 % [9].

В [10] были проведены экспериментальные и численные исследования теории турбин Дарье и Савониуса с диаметром 183,6 и 180 мм соответственно. КПД был выше у турбины Дарье. По мере увеличения числа и начального угла атаки лопаток турбины повышались коэффициенты мощности и давления вследствие приращения кавитации [11].

Производство электроэнергии на гидроузлах с низким напором имеет ограничения, что недостаточно для эффективной работы. Работа прототипа медленная и неэффективная при низком уровне напора в случае турбин большего диаметра, так как они потребляют значительную энергию во время работы, как с конструкцией V-образного манжетного уплотнения. Эффективность низкая и колеблется в пределах от 54 до 56 % [12]. Вследствие фиксированного размера стандартных фитингов некоторые ограничения связаны с диаметром турбины и выходным сечением сопла [13]. Учитывая этот фактор, был разработан тип турбины Z-blade для работы в условиях очень низкого напора воды [14].

Здесь вместо труб из оцинкованного железа используются стандартные фитинги из серого ПВХ класса D. Они по сранению с трубами недороги, легко доступны и могут быть легко модифицированы или отрегулированы, чтобы соответствовать указанному диаметру турбины [15]. Надо отметить, что турбина с Z-образной лопастью оказалась более рентабельной и ее общая стоимость составляет 76 долларов США, что почти вдвое меньше по сравнению с другими типами.

Благодаря более простой технологии изготовления продолжительность сборки турбины короче. Следовательно, это обеспечивает более дешевую себестоимость. Самая дорогая часть – это водяная муфта. Процесс сборки также прост, не требует наличия передовых технических знаний, привлечения высококвалифицированных специалистов.

Рациональная идея Эйлера о конструкции гидротурбин нашла свое окончательное выражение в его предложении разделить гидравлическую машину нового типа на две части – неподвижную и вращающуюся. Неподвижная часть представляет собой отводящее устройство, направленный поток воды из нее поступает в нижнее вращающееся колесо, закреплённое на валу вращающегося рабочего колеса, а вода выходит оттуда через 20 изогнутых труб. Эта конструкция была переходной конструкцией от оригинальной формы колеса Сегнера к гидравлической турбине.

Материалы и методы

260–270 лет спустя после Бернулли были разработаны новые конструкции перехода от колеса Сегнера к гидротурбине. Один из них, трубчато-лопастное рабочее колесо [15], содержит двойной диск и лопасти в виде вогнутых труб с ограничением поверхности вхо-– 934 – да. При вращении рабочего колеса вертикально загруженный столб воды тоже вращается, в результате наблюдается перпендикулярность направления абсолютной скорости воды относительно переносной скорости рабочего колеса. Следовательно, наблюдается увеличение гидравлического и местного сопротивления для входа воды в лопастные трубы. Здесь полностью не используется кинетическая энергия потока, увеличивающаяся при падении под влиянием силы тяжести воды.

Авторами предложена реактивная гидротурбина с соплом, и для определения ее техникоэкономической эффективности разработаны два типа реактивных гидротурбин, различающихся направляющим устройством. Первый тип, сопловая реактивная гидротурбина, содержит рабочее колесо – крыльчатки, жёстко закреплённое ко дну цилиндра, каналы для оттока воды и статор с отражателями. С целью повышения КПД за счет улучшения реактивной отдачи и упрощения конструкции корпус рабочего колеса выполнен в виде цилиндра, лопасти и каналы для оттока воды расположены на одной горизонтальной плоскости дна рабочего цилиндра. Каналы для оттока воды представляют собой сопла с конфузором, обеспечивающим равномерное сжатие воды на выходе канала. Водовыпускной канал сопла изогнут под углом 90°, расположен перпендикулярно внутреннему радиусу в горизонтальной плоскости рабочего колеса, которое позволяет перпендикулярно направить выходящий из сопла поток воды на касательную плоскость в точке центра дуги вогнутого и вертикально установленного кругло-цилиндрического отражателя [18].

Результаты и обсуждение

Аналитически определены функциональные соотношения между геометрическими и энергетическими параметрами этой гидротурбины. Уравнение Навье-Стокса в цилиндрической системе координат решалось с использованием соответствующих начальных, граничных условий и уравнений неразрывности. С помощью функции распределения воды по скоростям определены коэффициент Кориолиса и средние скорости в нем для формы гидротурбины [18]. Для важных сечений гидротурбины решались уравнения Бернулли, на основе уравнений неразрывности определялись средние скорости потока воды, теоретически рассчитывались потери энергии на гидравлические и местные сопротивления [19].

Ниже представлена общая схема вида сверху на поперечное сечение рабочего колеса гидротурбины в горизонтальной плоскости. Для наглядности количество сопел равно четырем. Количество сопел может быть различным в зависимости от размеров конструктивных частей гидротурбины (рис. 1).

Приравняв массы воды, поступающей и выходящей из гидротурбины, для определения наименьшего значения диаметра d 1 водоподводящей трубы гидротурбины получим следующее выражение:

^^Ж^ = МлгХ. (1)

Расчет через поверхность имеет вид:

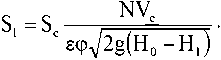
Определим диаметр трубы, поставленной на входе воды в гидротурбину, следующим образом:

dx = ^

Q

.

Здесь ε – коэффициент, представляющий собой отношение «живой» площади поперечного сечения воды при входе в гидротурбину и поперечного сечения водоподводящей трубы; φ – коэффициент, соответствующий типу сопла, установленного на входе воды в гидротурбину; N – количество сопел; S_c – выходная поверхность сопла; H₀ – полное давление воды; H₁ – потеря давления воды, соответствующая размеру гидротурбины; V c – скорость водяной струи при выходе из гидротурбины; Q – расход воды.

В результате решения уравнений Бернулли для скорости воды V 3 , поступающей в сопло гидротурбины, и скорости V_c, выходящей из него, был получен следующий результат:

;

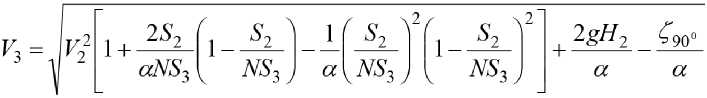
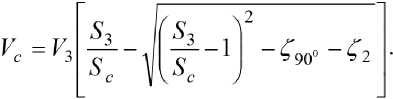
Для определения гидравлических и местных потерь энергии в гидротурбине определялся режим течения воды. Если принять высоту водяной струи H₀=2 м, скорость воды на входе в турбину V 0 =5,95 м/с, d=0,273 м, коэффициент динамической вязкости при температуре 15 °C

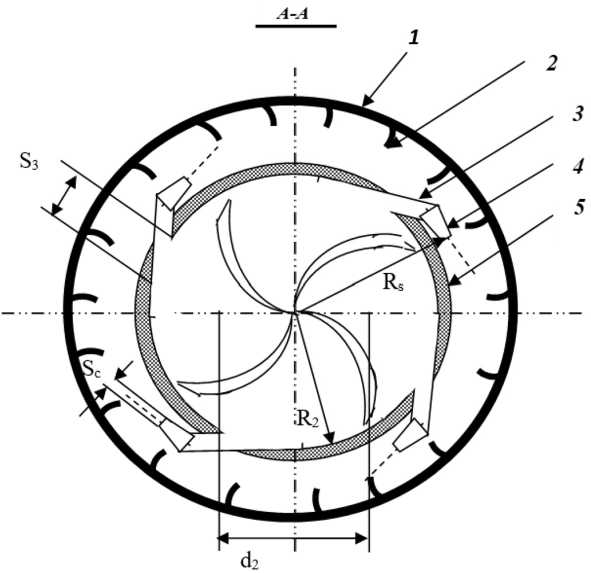
Рис 1. Общая схема поперечного сечения рабочего колеса гидротурбины в горизонтальной плоскости (вид сверху)

Fig 1. The general scheme of the cross-section of the impeller of the hydraulic turbine in the horizontal plane (view from above)

равен 0,0114 [20], число Рейнольдса Ке = ^ , получим значение Re=140921. Видно, что течение воды внутри гидротурбины имеет турбулентный характер.

λ – значение коэффициента Дарси зависит от степени шероховатости трубы и числа Рейнольдса. В этом случае можно использовать формулу Никурадзе (105≤Re≤108) для жидкости, текущей в турбулентном режиме в гладкой трубе при установившемся течении:

X - 0,0032 + 0,22 Re"0’237 - 0,0 1 65

С помощью этого коэффициента вычисляем потери энергии на трение:

^.^=05165:U ^ = 00605 ^ d 2g 0,3 2g         2g

Так, при турбулентном движении внутри гидротурбины кинетическая энергия потока жидкости теряется не более 6 % за счет трения [20].

Коэффициент сопротивления ζ2, вызванного равномерным сжатием и трением воды в конфузоре сопла, определяли по следующей формуле [22]:

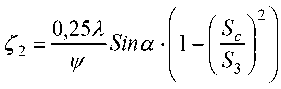
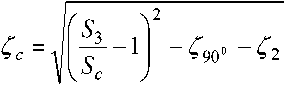
где α=300 – угол конусообразования; ψ – коэффициент пропорциональности, равный 2 для труб и 1 для прямоугольных фигур; λ – коэффициент Дарси.

Крутящий момент, создаваемый на рабочем колесе устройства, обусловлен струей, создаваемой водой, выходящей из сопла, и активной силой давления на внутреннюю лопатку, обусловленной изменением импульса воды. Расчет этой величины определяется относительно неподвижной системы отсчета, связанной с землей, и подвижной системы отсчета, связанной с центром рабочего колеса.

Согласно общей теореме об изменении кинетического момента твердого тела при сложном движении [22]:

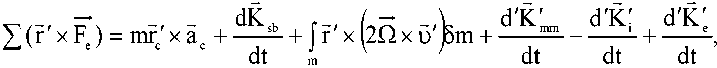
где заштрихованные выражения представляют величины, полученные относительно подвижной системы отсчета, расположенной в центре масс рабочего колеса.

Через следующие величины обозначили: rʹ – радиус-вектор от центра рабочего колеса до водовыпуска; δm – количество воды, выходящей из контролируемого объема; ас – ускорение центра масс наблюдаемой системы относительно неподвижной внешней системы отсчета; r' – центр масс рассматриваемой системы; – изменение во времени кинетического момента dK'

рабочего колеса и водной системы как единого твердого тела; – учитывается измене- ние кинетического момента движущейся массы внутри рассматриваемого объема во времени, а выражение под интегралом представляет собой момент силы, возникающий за счет силы

Кориолиса, вызванной вращением системы; ,     – соответственно, изменение во времени dt dt кинетических моментов количества движения воды, входящей и выходящей из наблюдаемого объема.

Столб воды оказывает давление на воду внутри рабочего колеса, в результате этого увеличивается скорость водного потока за счет изменения статического давления в коническом сопле.

Пусть скорость воды, поступающей в конфузор, равна υʹ , а скорость на выходе υ c .

Поскольку рабочее колесо вращается вокруг неподвижной оси, а0=0, то первый член в левой части уравнения (9) равен нулю. Если рассматривать цилиндр, сопло и количество воды внутри них как единое целое твердое тело в рассматриваемый момент времени, когда рабо чее колесо вращается с постоянной скоростью относительно оси вращения, то --- = I--= 0. dt dt d'K'

В динамически уравновешенном потоке воды – изменение во времени кинетического момента движущейся массы в рассматриваемом объеме равно нулю. В результате уравнение (9) принимает вид:

^(r'xFJ =jr' x ^2Q x 6'^51

, dt dt dt

При вычислении интеграла, выражающего силу Кориолиса в этом уравнении, если учесть влияние силы реакции (Ω× υʹ ) и параллельности r′, создаваемой импульсом струи воды, выходящей из сопла, получается следующее выражение:

jf'x (2Qx б'Ьт = 2-^coz f xdx = —(oz(R2+hc)2.

i V Г dt z             dt

В выходное отверстие сопла извне вода не поступает, поэтому изменение ее импульса во времени равно нулю:

Изменение количества движения массы воды, выходящей из сопла за время dt:

d-к;

r— г -dm.

,Кз +hc lxuc----

Подставляем полученные выражения в (8) и вычисляем момент силы относительно центра вращения частицы воды, вылетающей из сопла. При решении этого уравнения результирую- щая величина импульсных моментов системы, возникающих в результате внутреннего взаимодействия, равна нулю.

Изменение во времени импульсного момента гидротурбины под действием внешних сил и с учетом следующих условий находим через следующие формулы:

co = ———cos В; и = и cos В; и = 0;

z R2+hs P ' a P v ’

p = arcos^; dms = рл(К2+hs)2usdt, Rst находим проекцию момента силы, возникающей в одном сопле в направлении OZ:

M₂=-R,^(_Us-a>_zRj,     R s =R 2 +h s .                (14)

dt

В результате, решая уравнение (8), получаем необходимое выражение для момента силы, действующей в единицу времени [22]:

Mz = -N7ipRs'us (us - cozR s) = -NupR’ us2 (1 - cos P) ,             (15)

определяя выражение для импульса реактивной мощности, возникающего в сопле, решая совместно с выражением (15), находим циклическую частоту ω z рабочего колеса:

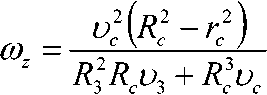
При этом, R c – расстояние от оси вращения до центра водовыпускного патрубка; r c – радиус выходного отверстия сопла; υ 3 , υ c – соответственно скорости воды на входе и выходе из сопла.

Таблица 1. Изменение энергетических параметров гидротурбины в соответствии с ее геометрическими размерами

Table 1. Changing the energy parameters of a hydro turbine in accordance with the geometric dimensions of the turbine

Н 0 , м	V 0 , м/с	V 1 , м/с	V 3 , м/с	V C , м/с	ω, рад/с	P, Вт	M, Нм	КПД, %	n s , об/мин	Q, л/с
1	3,26	2,91	3,42	6,33	9,92	988,91	55,19	59,85	166,15	168,43
2	5,32	4,58	5,14	9,51	17,01	2371,26	74,07	67,54	296,85	178,93
3	6,79	5,78	6,42	11,87	23,21	3762,53	85,11	70,12	409,96	182,32
4	7,98	6,77	7,48	13,83	28,36	5156,11	93,14	71,42	513,35	183,99
5	9,03	7,64	8,41	15,54	34,80	6550,67	99,55	72,19	610,17	184,99
6	9,96	8,42	9,24	17,09	39,71	7945,73	104,95	72,71	702,09	185,65
7	10,81	9,13	10,01	18,50	43,21	9341,09	109,63	73,08	790,15	186,13
8	11,60	9,79	10,72	19,82	48,36	10736,64	113,78	73,36	875,04	186,48
9	12,34	10,40	11,39	21,05	54,23	12132,33	117,53	73,58	957,27	186,76
10	13,04	10,99	12,02	22,22	58,85	13528,11	120,95	73,75	1037,20	186,98

Таблица 2. Параметры мощности при изменении уровня воды без изменения размеров гидротурбины

Table 2. Changing the power parameters when the water level changes without changing the size of the turbine

Н 0	V 1 , м/с	V 2 , м/с	V 3 , м/с	V C , м/с	ω, рад/с	P, Вт	M, Нм	F, Н	Q, л/с	КПД, %
1	3,3	2,7	3,2	6,5	11,2	4311,6	384,2	6933,8	762,3	57,7
2	5,3	4,3	4,8	9,6	16,6	14028,6	843,7	15224,9	1129,6	63,3
3	6,8	5,4	6,0	11,9	20,7	26929,6	1303,2	23516,0	1403,8	65,2
4	8,0	6,3	6,9	13,8	24,0	42361,4	1762,7	31807,2	1632,7	66,1
5	9,0	7,1	7,8	15,5	27,0	59961,4	2222,1	40098,3	1833,1	66,7
6	10,0	7,9	8,5	17,0	29,6	79489,2	2681,6	48389,4	2013,8	67,1
7	10,8	8,5	9,3	18,4	32,1	100770,6	3141,1	56680,5	2179,5	67,3
8	11,6	9,1	9,9	19,7	34,3	123671,2	3600,5	64971,7	2333,4	67,5
9	12,3	9,7	10,5	21,0	36,5	148083,9	4060,0	73262,8	2477,9	67,7
10	13,0	10,3	11,1	22,1	38,5	173920,2	4519,5	81553,9	2614,3	67,8

В табл. 1–2 представлены энергетические параметры гидротурбины по результатам теоретического расчета.

Анализировать изменение энергетических характеристик гидротурбины в зависимости от ее габаритов можно на основании табл. 1. Из таблицы видно, что с момента входа в сопло поток воды движется в области конического сужения с прямым поворотом. При этом скорость воды непрерывно увеличивается при наименьшем сопротивлении, в результате чего наблюдается увеличение крутящего момента. В результате повышается полезная мощность и частота вращения. При увеличении высоты воды через 3 метра изменение коэффициента полезной работы уменьшается, а через 6–7 метров увеличивается на очень небольшую величину. По мере повышения скорости системы с увеличением высоты эффективный импульс воды, выходящей из нее, уменьшается, и она достигает частоты вращения в динамическом равновесии.

Если обратить внимание на табл. 2, то наблюдается, что при увеличении высоты водяного столба без изменения габаритов гидротурбины расход воды становится больше за счет увеличения скорости воды на выходе из сопла. В этом случае при дефиците воды КПД гидротурбины будет очень мал.

При достаточном запасе воды частота вращения гидротурбины будет достигать своего критического значения при дальнейшем увеличении высоты. После этого КПД гидротурбины остается неизменным, так как сила сопротивления на ней возрастает пропорционально квадрату скорости. Использование таких гидротурбин в местах, где есть возможность увеличить количество воды, дает хорошие результаты.

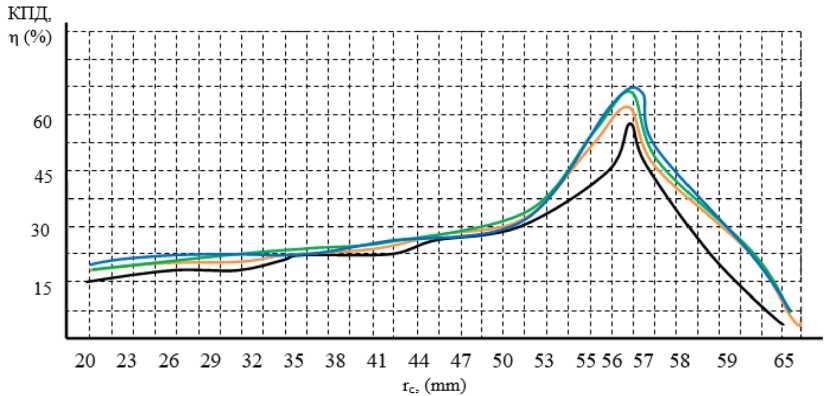
Рис. 2. Зависимость КПД от водовыходного радиуса сопла без изменения габаритов гидротурбины [22]

Fig. 2. Dependence of efficiency on the water outlet radius of the nozzle, without changing the dimensions of the hydraulic turbine [22]

Из рис. 2 видно, что гидротурбина работает с высоким КПД только в том случае, когда радиус выходного отверстия сопла находится на своем критическом значении, соответствующем заданному количеству воды.

Выводы

В результате проведенного теоретического и практического исследования получили следующие выводы:

• –    при увеличении высоты водяного столба без изменения габаритов гидротурбины расход воды увеличивается за счет повышения скорости воды на выходе из сопла. В этом случае при дефиците воды КПД гидротурбины будет очень мал;

• –    гидротурбина работает с высоким КПД только в том случае, когда радиус выходного отверстия сопла находится на своем критическом значении, соответствующем заданному количеству воды;

• –    реактивная гидротурбина на основе колеса Сегнера резко отличается от существующих активных и реактивных гидротурбин своим быстродействием и высоким КПД. При изменении размеров рабочего колеса гидротурбины по высоте водяного столба КПД составил 67 % при напоре воды 2 метра. При увеличении напора воды её КПД повышается до 74 %;

• –    установка в сопле конфузора с углом формирования конуса 30⁰ привела к увеличению реактивной силы, создаваемой в сопле;

В заключение можно сказать, что мнение великого ученого Эйлера о будущем гидротурбины на основе колеса Сегнера подтвердилось.