Реализация ациклической диаграммы Смейла омега-устойчивым диффеоморфизмом поверхности

Последовательность, состоящая из базисных множествЛ/ =Л.,Л.,...,Л^ =Лj(k_1), такая что Л -<л. ^■■■Л\ называется цепью длины k ∈  , соединяющей периодические орбиты Лi и Лj.

Такая цепь называется максимальной , если в нее нельзя добавить ни одного нового базисного множества. Цепь называется циклом , если Л i =Л j .

Диффеоморфизм f : Mⁿ >  Mⁿ называется О -устойчивым , если C ¹ - близкие к f диффеоморфизмы топологически сопряжены на неблуждающих множествах. Согласно [3], диффеоморфизм f : Mⁿ >  Mⁿ является Q -устойчивым тогда и только тогда, когда он удовлетворяет аксиоме А и не имеет циклов.

Диаграммой Смейла A _f О -устойчивого диффеоморфизма f : Mⁿ >  Mⁿ называется граф, вершины которого соответствуют базисным множествам, а ориентированные ребра последовательно соединяют вершины максимальных цепей.

В дальнейшем под направленным циклом ориентированного графа будем понимать замкнутый путь, пройденный в соответствии с направлениями ребер ([6]). Граф называют ациклическим , если у него нет направленных циклов. При этом не исключаются ``параллельные'' пути, которые выходят из одной начальной вершины и приходят в одну конечную, но при этом не совпадают.

В работе ([2]), в качестве проблемы сформулирован следующий вопрос: какие диаграммы могут соответствовать О -устойчивым диффеоморфизмам?

Настоящая работа дает частичный ответ на этот вопрос в виде доказательства следующей теоремы.

Теорема. Любой связный ациклический граф реализуется О -устойчивым диффеоморфизмом поверхности .

Построение базисных множеств для диффеоморфизма двумерного тора. Диффеоморфизм Аносова на 2-торе. Пусть C е GL(2,0) - гиперболическая матрица с собственными значениями \, Л2 такими что Л =\Л |> 1 и 1 Л2 \=1 /Л. Так как матрица C имеет определитель, равный 1, то она индуцирует гиперболический автоморфизм C: T2 > T2 с неподвижной точкой O. Этот диффеоморфизм является диффеоморфизмом Аносова, обладающий двумя трансверсальными инвариантными слоениями (устойчивым и 2

неустойчивым), любой слой каждого из которых всюду плотен на торе. Кроме того, множество периодических точек диффеоморфизма C также плотно на T ² .

«Хирургическая операция» Смейла. Пусть а :□ ^ [0,1]

функция, заданная

формулой (см. рис. 1)

0,

^{а (} x ) =

Л ’³ + 1

- - x

' - ^'f( x — f

+ V

2 -3 ^x „ ^Л ,

Л ^- <  x <  1, x ^1.

1Л

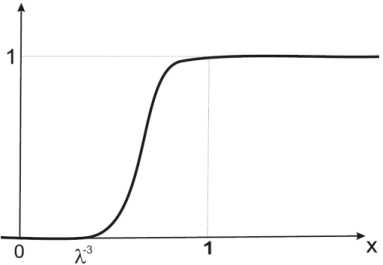
Рис. 1. График функции а ( x ) .

Определим функцию v : [0,1] ^ [0,1] формулой (см. рис. 2)

Л x ,                    0„ x „ Л^- ,

^ ( x ) x + (1 — а( x )) Л² x ,   Л^-<  x„ 1.

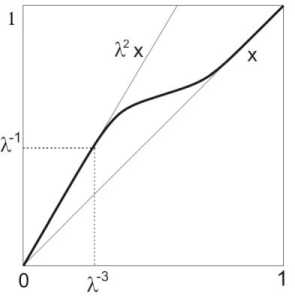
Рис. 2. График функции v ( x ) .

Продолжим функцию V нечетным образом на отрезок [ — 1,1] , положив v ( — x ) = — v ( x )

для x e [0,1] .

Положим D - {(x, У) ^ □ 21 x2 + y2„ 2}. Определим функцию YA : D ^ [0,1] формулой

0„ | y |„ Я ’³, Я "³<  x „ 2.

^ (1 У I) x ^{+ (1} - ^ ⁽l У ^{|) v (} x ),

Определим диффеоморфизм  BA : D ^ D формулой  BA(x, У) - (YA(x, УX У).  По построению, BA(x, У) - (^2 x, У), если x2 + У2„ Я 6 и является тождественным на dD.

Пусть x , У - локальные координаты в окрестности U ( O ) точки на T ² такие, что диффеоморфизм C в этих координатах имеет форму C ( x , у ) - ( x / Я , Я у ) . Тогда Ox с W O и

Оу с W u , а также { y - const } и { x — const } являются устойчивым и неустойчивым слоениями. Определим диффеоморфизм В_А : T ² ^ T ² , совпадающий с диффеоморфизмом B A внутри окрестности U (0) и тождественный вне этой окрестности. Тогда согласно [4], [1], диффеоморфизм ^¥_а - ]В_А ° C является DA-диффеоморфизмом, неблуждающее множество которого состоит из одномерного аттрактора A, обладающего единственной связкой степени

2 c двумя различными граничными неподвижными p1 и p2, и источниковой неподвижной точкой а (см. рис. 3).

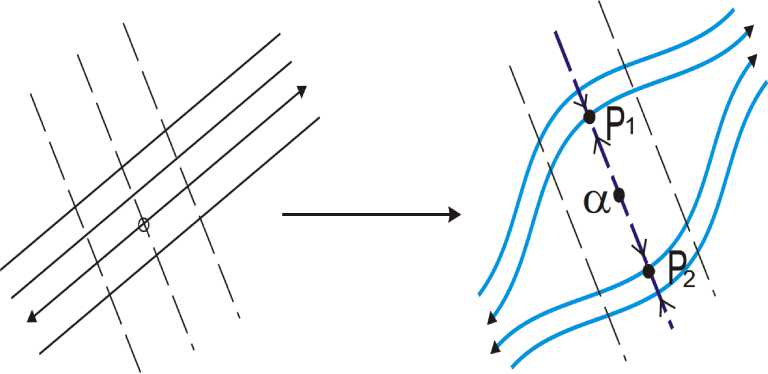
Рис. 3. «Хирургическая операция» Смейла.

Модельные диффеоморфизмы на торе. В этом разделе, используя хирургическую операцию Смейла, мы построим модельные диффеоморфизмы на двумерном торе.

Диффеоморфизм F m m . Выберем k eD периодических орбит O 1,•••^, O k диффеоморфизма Аносова О периодов m1,■■■ , m k , соответственно. В окрестности каждой орбиты произведем хирургическую операцию Смейла вдоль устойчивого слоения.

Полученный диффеоморфизм F_mi : T ² ^ T ² имеет единственный нетривиальный одномерный аттрактор Л m , . , m и k периодических источниковых орбит a m ,",a периодов m1,...,mk , соответственно.

Диффеоморфизм р’^"n l . Выберем l еП периодических орбит O \•••, O диффеоморфизма Аносова C периодов n1,•■•,n_l , соответственно. В окрестности каждой орбиты произведем хирургическую операцию Смейла вдоль неустойчивого слоения. Полученный диффеоморфизм F”'”"n^l : T ² ^ T ² имеет единственный нетривиальный одномерный репеллер Л n ¹”" ’ ”^l и l периодических стоковых орбит ft ” ,•••, & ” периодов ” 1 , ■ ”,”_l , соответственно.

Диффеоморфизм F¹ "^ • Выберем l + к еП периодических орбит O ' , . , O k , O , " , O диффеоморфизма Аносова C периодов m',•••,m k , ” ' , — , ”_l , соответственно. В окрестности каждой орбиты O ' , " , O k произведем хирургическую операцию Смейла вдоль устойчивого слоения и в окрестности каждой орбиты O ', ", O^l произведем хирургическую операцию Смейла вдоль неустойчивого слоения. Полученный диффеоморфизм F ” "" ^ : T ² ^ T ² имеет единственное нетривиальное нульмерное базисное множество Л ” 1 ’ ’ ” l ^, k периодических источниковых орбит a m , " , a периодов m ' ,...,m k и l периодических стоковых орбит m_v " , m k периодов ” ' , • , ”_l , соответственно.

Примеры модельных диффеоморфизмов F_{2 3} , F ' ^,4, F ^ изображены на рисунке 4.

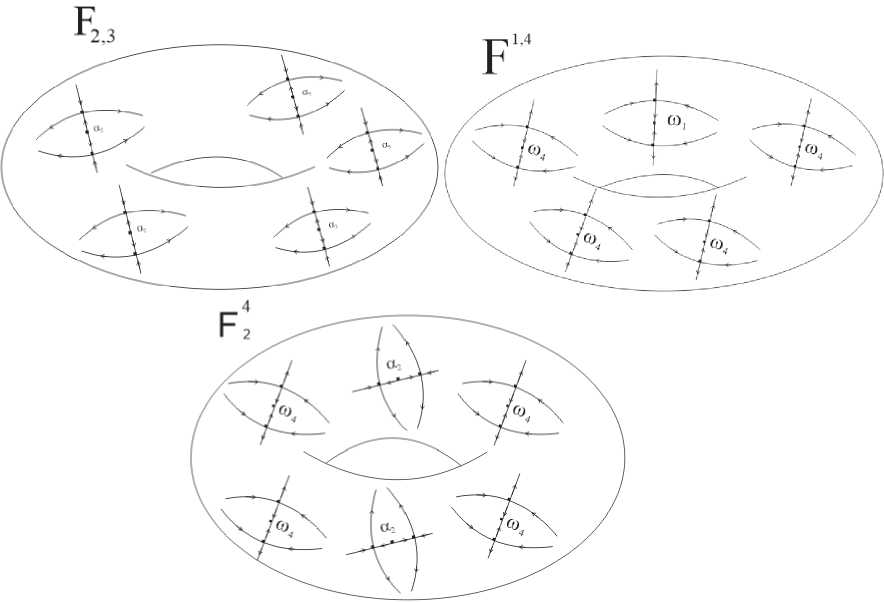
Рис. 4. Модельные диффеоморфизмы F 2 3 , F ^1,4, F .

Доказательство основного результата. В настоящем разделе мы реализуем диаграмму Смейла Ω -устойчивым диффеоморфизмом поверхности.

Распределение вершин графа по уровням. Так как в графе Г нет направленных циклов, на нем можно ввести частичный порядок. Упорядочим вершины графа по следующему принципу:

• •     уровень B о состоит из вершин b °,..., b q ⁰ , в которые не входит ни одно

ребро;

• •     уровень Br состоит из вершин b,,...,b q , в которые входят, только ребра

из вершин уровней B ₀ , . , B_r - 1 ,

• •     последний уровень Bp состоит из вершин b⁰_р,---,bq^p , из которых не

выходят ребра (см. рис. 5).

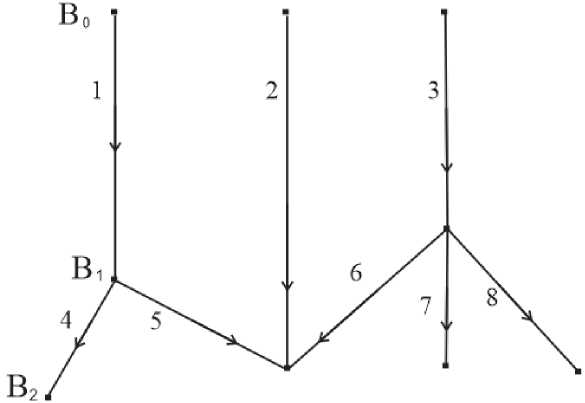
Рис. 5. Распределение вершин по уровням.

Перенумеруем ребра графа в произвольном порядке: каждому ребру ( b j ,b j ² ) поставим в соответствие некоторый номер jj ² , то есть каждое ребро будет определяться тройкой ( b j, b f^ ² , J ) .

Реализация вершин уровня B0. Для каждой вершины bj и каждого выходящего ребра положим   ni = kjj и  fj = F j. Обозначим через  ojj  стоковую орбиту, соответствующую выходящему ребру  (bj,bj,kj,j). В примере графа на рисунке 5, f0 = F1,Fb. = F2,f2 = F3. b0              b0              b0

Реализация вершин уровня B_r . Для каждой вершины b ^j и каждого входящего ребра ( b j , b f , J ), i = 1,..., № _r положим m i = k jj .     Для     каждого     выходящего     ребра

r            № источниковую орбиту, соответствующую входящему ребру (bj, b, kj ’rJ) и через ^’j -стоковую орбиту, соответствующую выходящему ребру (bj, bj, j). В примере графа на рисунке 5, f0 = Fl4,5, f = F,6,7,8.

Реализация вершин уровня B _p . Для каждой вершины b ^j и каждого входящего ребра

( b j , V , k j ’ ^J ), i = 1,..., u^Jj положим     m. = k^j ’ ’    и f = f      . Обозначим через     a_r 'j '

4 ri     p    ri, r 7         p          p                               i       /r, r                     ь hJ         ml,., m j                                       1                ri, P p               Mp источниковую орбиту, соответствующую входящему ребру (bj, bJp, kj/ ) .

В примере графа на рисунке 5, f b , = F4’ f^ = F256’ f^ ^ = F^ f^ з = F .

Склейка динамики вдоль ребра графа Г. Каждому ребру (bj,Ь2,ЬЬJ2) графа Г r^r^r , r однозначно соответствует стоковая орбита юJ1,rJ2 диффеоморфизма f и источниковая r1, r2                                     by орбита aj’rj2 диффеоморфизма fj2 . Обе орбиты имеют одинаковый период jj2. Покажем, как склеить динамику вдоль ребра (bj, Ь2, kj,J2). rl        '2        rl, r2

Выберем окрестностиUj,j2, VjJ2, содержащие орбиты (jj,2,aj’rJ2,соответственно, и такие,            что             fй (Uj1 ,j ) c intUj1 ,j ,V ,j о int f,, (Vj1 ,j).             Положим

J bj1 V    rl , r2  7                rl , r2  ’  rl, r2               b bJ2 V  rl, r2'

rlr xj1,j - Uj"j2, int j AUj"j2 Yj"j       Jl^jintv j"j2. Оба множества состоят из

Г’ r2          Г’ r2   ,         bbJl\ rX, r2  7’  rl ’ r2       b bJ 2 Vr r, r2     ,            rl’ r2

rl одинакового количества двумерных колец. Обозначим через  H,j2 : Xj,j2 4 Yj’j2

г , '2            r , '2'1 ’ r 2

диффеоморфизм такой, что н² ’ ^j2°f. I = f II ’ ^{j 2} I .

,               r l ’ r 2 bp Id U ^j , ^{j 2}      b _bJ ²        r l ’ r 2 Id U j , ^{J 2} .

На рисунке 6 введенные объекты изображены для ребра (b0, b0, l) графа, приведенного на рисунке 5.

Положим

Q j ’ ^{J 2} = (T ² ,   int f_hJ, (U j ’ ^{J 2} )) т (T ² ,   intV j^{j 2} )

r l , r 2                                                b^J l           r l ’ r 2                                '                    r l , r 2 ⁷

r l

и

Q J'J = (T² ,   intf b J l (U r'j ² )) и H j , J 2 (T² ,   intV j/ ² ).

r                                        r l ’ r2

Обозначим через p j,^{j 2} : Q ^j ’ j ² 4 Q j , j ² естественную проекцию.

• ⁷ r l ’ r 2     ^r l ’ r 2         *r l ’ r 2                         J       X        '

Склейкой динамики вдоль ребра (bj, bj, kj'j2) графа Г назовем диффеоморфизм fhr 2 : QQj’J' 4Q^j2.2, совпадающий с диффеоморфизмом  jy-h f (jy-hу'i          на b rl ’ r2    lr ’ r2       ^rl ’ r2  ,                                           TT        KT                pl, r2 . J, J2 pr rx , r /   j j ’J2(t2  vjl ^2)

r 2                              p rl , r 2 ^{( ,} r l, r 2 )

P^J j ^{2( T 2} • V j  ) ^{и с} ди^ффеомор^физмом P J P 4) ^l I J l , J _2(T2 jp ,y на P^j 'J^{(T 2} • U г ^Л).

b r                         ^pr\ , r> ^(T ’ U r , r> )

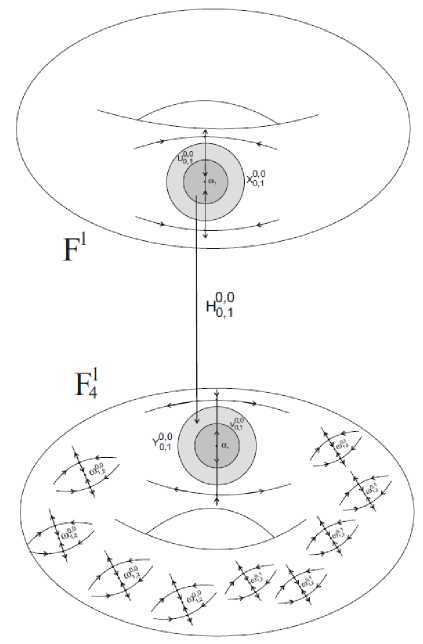
Рис. 6. Объекты, связанные с ребром ( b 0 , b 0 ,1) .

Построение результирующего диффеоморфизма. В построенных по графу Γ моделях существует взаимно однозначное соответствие между стоковыми и источниковыми орбитами.

Именно стоковая орбита rn j¹^j ² диффеоморфизма f соответствует источниковой < 1 , r ²                                         b^

орбите   a, j ² диффеоморфизма f_{bJ 2}. Обе орбиты имеют одинаковый  период k j².

b r2

Результирующий диффеоморфизм f : M ² ^ M 2 представляет из себя склейку динамики вдоль всех ребер графа Г .