РЕАЛИЗАЦИЯ АКУСТОЭЛЕКТРИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ. 1. ЗАВИСИМОСТЬ ЭЛЕКТРОКИНЕТИЧЕСКИХ ЯВЛЕНИЙ В ВОДНЫХ РАСТВОРАХ ЭЛЕКТРОЛИТОВ ОТ СТРУКТУРЫ МЕМБРАННЫХ МАТЕРИАЛОВ

Ранее в серии работ авторов [1–3] было представлено успешное использование электрокинети-ческого явления "потенциал течения" (потенциал протекания) в воздушной среде при реализации электрокинетического акустоэлектрического преобразователя (ЭАП). Для реализации ЭАП в условиях жидкой среды необходимо проведение дополнительных исследований, учитывающих особенности протекания в ней явления потенциала течения. Так, в жидкой среде, в отличие от воздушной среды, возникает возможность варьирования свойств двойного электрического слоя (ДЭС), в частности, с помощью величины его важнейшей характеристики — ζ -потенциала, которая существенно зависит от концентрации и вида электролита в жидкости. Кроме того, электрокинетические процессы существенно зависят от соотношения толщины диффузного слоя δ и характерного размера пор a пористой структуры.

Настоящая работа посвящена изучению этих зависимостей в конкретном случае пористой структуры, заполненной электролитом.

ФЕНОМЕН ПОТЕНЦИАЛА ТЕЧЕНИЯ

Ниже приводятся некоторые необходимые для дальнейшего изложения дополнительные сведения о явлении "потенциал течения".

Потенциал течения (протекания) — одно из классических электрокинетических явлений, возникающих при наложении на заряженную капиллярно-пористую систему (это может быть диафрагма, мембрана, капилляр или система капилляров) внешних градиентов. Потенциал течения — это разность электрических потенциалов при нулевом суммарном электрическом токе, вызванная протеканием заряженной жидкости под действием градиента внешнего давления и измеряемая между концами капилляров по системе в целом (см., например [4, с. 64–68]; [5, с. 4.25–4.28]; [6, с. 221– 225]; [7, с. 45–48]; [8, с. 182–190]). Используемые для измерений электроды должны быть одинаковыми и иметь небольшой (и желательно постоянный) потенциал асимметрии в исследуемом электролите.

Основная причина возникновения всех элек-трокинетических явлений — это существование ДЭС на границе раздела диэлектрик – раствор электролита. Если рассматривать в качестве модельной капиллярно-пористой системы одиночный капилляр, то наиболее существенным при проведении измерений является учет соотношения радиуса капилляра a и толщины диффузного слоя δ (в русскоязычной литературе используется и термин "приведенная толщина ДЭС", являющийся по смыслу более точным). На рис. 1 — представление границы раздела фаз в рамках классической модели Гуи [7, § 1.3]: плоская эквипотенциальная поверхность, ионы в растворе имеют конечный размер, но их заряд остается точечным.

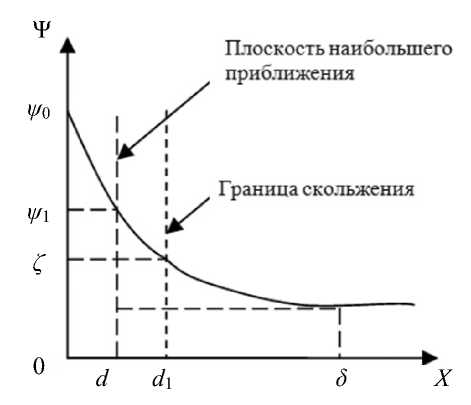
Рис. 1. Зависимость потенциала ДЭС от расстояния от поверхности.

На бесконечном удалении от поверхности потенциал равен нулю

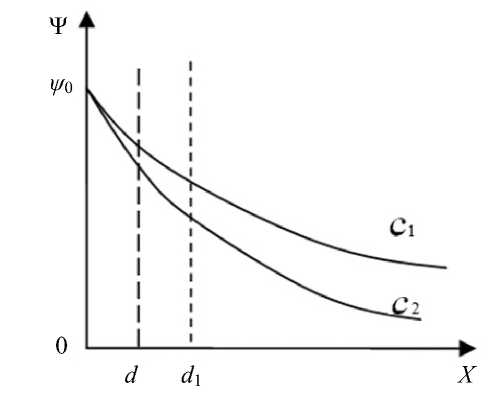
Рис. 2. Зависимость потенциала ДЭС от расстояния от поверхности при различных концентрациях элек-

тролита: С 1 <  c 2

В ДЭС рассматривают 3 электрических потенциала: поверхностный ψ 0 (называемый также термодинамическим потенциалом [8, с. 174]), ψ ₁ — потенциал плоскости, в которой располагаются заряды первого, ближайшего к поверхности слоя противоионов (его называют потенциалом плоскости наибольшего приближения, потенциалом плотного слоя, потенциалом штерновского слоя, потенциалом адсорбционного слоя — но смысл понятия в любом случае один), и электрокинети-ческий потенциал ζ , соответствующий границе скольжения — той границе, по которой происходит относительное перемещение жидкости и твердой фазы в электрокинетических явлениях.

В рамках этой модели величина δ — это координата, которая соответствует величине потенциала ψ ₁ / e (здесь e — число Эйлера). В исходной модели ДЭС Гуи – Чепмена, не учитывающей размера ионов, приведенная толщина ДЭС — это координата, которая соответствует величине потенциала ψ ₀ / e . Численное значение величины δ можно найти по выражению [9, с. 97]

1/2

я 0 RT

F 2 Z-■ c к      (i)        7

где z i — заряд иона; c i — его концентрация; ε — относительная диэлектрическая проницаемость; ε 0 — электрическая постоянная; R — газовая постоянная; T — абсолютная температура; F — число Фарадея.

Очевидно, что величина κ , обратная величине параметра Дебая 3 : к = 1 / 3, — это хорошо известный из теории сильных электролитов Дебая – Хюккеля параметр (обратный радиус ионной атмосферы). Видно также, что рост ионной силы раствора приводит к уменьшению приведенной толщины, этот процесс называют сжатием диффузной части ДЭС. При увеличении концентрации индифферентных электролитов (в случае электрохимически обратимых коллоидов, примерами которых являются ионные кристаллы, заряд и потенциал поверхности остаются практически постоянными) сжатие ДЭС приводит к уменьшению абсолютных значений ψ ₁ и ζ -потенциалов (рис. 2).

Если рассчитать величины δ для (1:1)-заряд-ного электролита при 20 ^оС, то для растворов с концентрациями 0.0001, 0.001, 0.01 и 0.1 М они будут равны 30.4, 9.6, 3.04 и 0.96 нм соответственно. В реальных системах при высоких концентрациях электролита, когда ДЭС сжимается до плотного слоя, электрокинетический потенциал может быть равным нулю (изоэлектрическая точка) при любом поверхностном заряде и потенциале, и в этом случае электрокинетические явления наблюдаться не будут.

Поскольку при анализе результатов электроки-нетических измерений важен учет соотношения радиуса капилляра a и толщины диффузного ДЭС δ , то в литературе часто используют термин "элек-трокинетический радиус" — безразмерный параметр ак ( к = 1/ 3 ). Все классические уравнения электрокинетики получены для систем с очень большими электрокинетическими радиусами , когда можно считать, что в середине капилляра

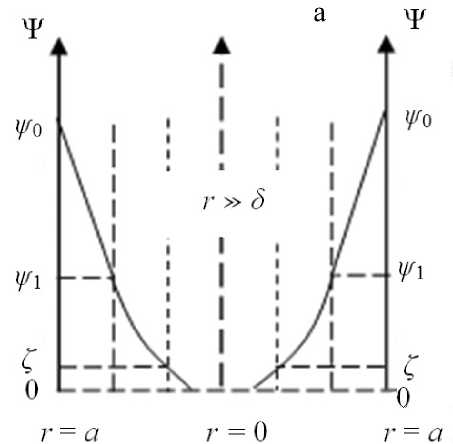
Неперекрытые ДЭС при больших a κ

Рис. 3. Структура ДЭС в капиллярах при различных электрокинетических радиусах

б

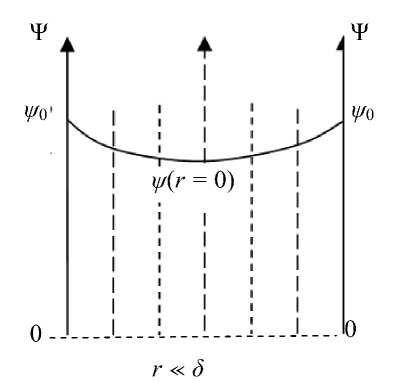
Перекрытые ДЭС при малых a κ

электрический потенциал практически равен нулю (например, если a = 10мкм, 5 = 10 нм, то а к = 1000). Если а к <  100, то говорят о перекрывании ДЭС в капиллярах, когда неравенство нулю электрического потенциала в центре поры начинает сказываться на измеряемых величинах элек-трокинетических параметров (рис. 3).

ОБОЗНАЧЕНИЯ ПРИ ФОРМАЛИЗАЦИИ ОПИСАНИЯ ФЕНОМЕНА

В работах, посвященных электрокинетическим явлениям вообще и потенциалу течения в частности, существует "разнобой" в системе обозначений. Это можно проследить при обращении к соответствующим разделам в работах [4–8]. Здесь будем следовать обозначениям, касающимся явления потенциала течения, принятым в классическом издании [10, с. 534, 535]. А именно: Ap — перепад давления на торцах капилляра; V — объем жидкости, протекающей через капилляр в единицу времени; I — сила тока в капилляре. Для потенциала течения в [10] принято обозначение Аф. Однако вследствие того что в электрокинетиче-ских явлениях электрические потенциалы принято обозначать символом ψ (см., например, [7, с. 10]), для потенциала течения здесь будет принято обозначение Ays. В качестве конкретного примера обозначений, приводящих к путанице, приведем обозначения, принятые, например, в [4, § 3.2]. Так, в формулах, описывающих потенциал течения, вместо акустического давления p фигурирует величина P = Ap /1, где 1 — длина капилляра, вместо потенциала течения Ays фигурирует величина ES.

Важное значение имеет отношение A y s / A p применительно к акустоэлектрическим преобразователям. В случае акустических полей величину A p можно трактовать как акустическое давление A p = p a , а разность потенциалов A y s равна электрическому напряжению U на электродах на обеих сторонах мембраны. В итоге справедливо ра-

Ay U венство ---=—. Величину U / pa принято

Ap   Га в акустике называть чувствительностью акусто-электрического преобразователя. Эта величина является важнейшей характеристикой акустоэлек-трического преобразователя: микрофона для атмосферных условий и гидрофона для жидкой среды. Она характеризует эффективность преобразования звуковой энергии в электрическую.

Далее будем придерживаться обозначений, принятых в [10], с учетом данного замечания.

АНАЛИТИКА ФЕНОМЕНА

На рис. 4, 5 представлены электрические схемы течения через капилляр.

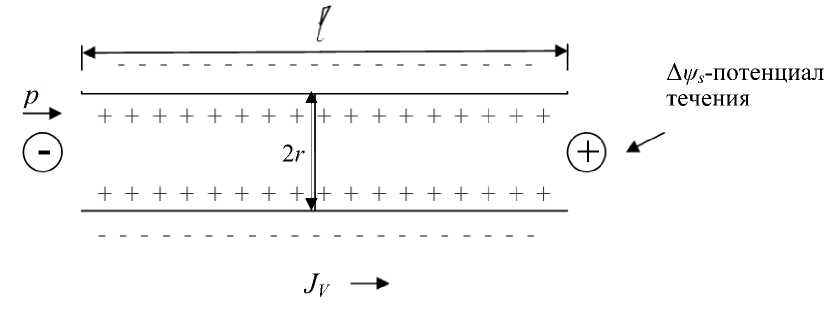
Рис. 4. Схема от рицате л ьно зар я ж е н н ог о капилляра в с т а ц ионарных ус л овиях п р и налож е ни и внешнего да в ления p .

J V — об ъ е мный пот о к жидкости

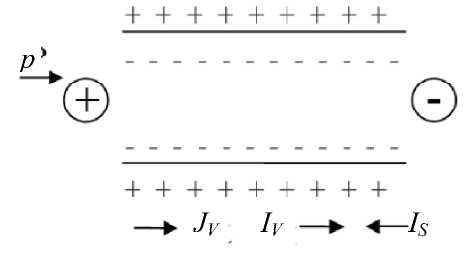
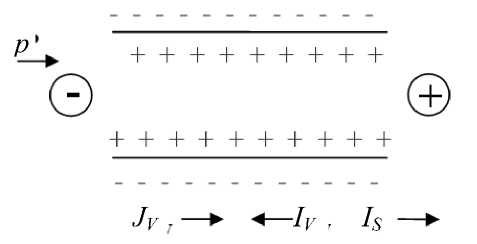
а

б

Рис. 5. Потенциал течен и я в п оложит е льно (а) и отрицательно (б) заряженном капилляре. С т ре лка м и по к азан ы напра в ле н ия потоков (пояснения в тексте)

При теоретичес к ом оп и с а ни и вели ч и н ы п оте нциала т ечени я A ^ s приняты с л е дую щ ие "договорен н ости":

• 1.    Потенциал те чения A ^ s считается положительным, есл и о н бо л ьше с о сторон ы б ол е е высокого д а вле н ия.

• 2.    Ток тече н ия I_s — электрическ и й ток, возникаю щ ий п ри д в и ж е н и и з аряж е н н ой жид к ости при на ло жении в нешнего д авлен и я, с чи та е тся положительным, е с ли он н а пра в лен в сторону низк ог о да в лени я. Нап ра в л е н ие любого э лек три ческог о тока, как об ы чн о п ри ня то в ф и зи к е, — это направлен и е дви ж е н ия катионов.

• 3.    Объемн ы й ток I_V — электромиграционный э л ектриче с кий ток, в озн икаю щ ий в электрическом поле п отенц и ала т ечени я A ^ S , положительным

• 4.    В стационарном состоянии I V + I s = 0 (с учетом знака).

• 5.    При более в ысок о м давлении с ле ва от к а пи лляра (как на рис. 5) V p < 0 (сторона П - сто ро н а Л).

объемн ы й ток та кж е с чи та е тся в том с л у ча е, когда он на п равлен в с то рону н и зкого давл е ния.

Для широких капилляров ( не п ере к рыты е ДЭ С ) выражение д л я ток а те ч ен и я в к ру говом цил и ндриче с ком ка п и л ляре мо жно пол у чить (см., например, [8, с. 184]):

££ 0 A ^z A p

I s =--Г’

ηl

где A — площ а дь, через которую течет ток , η — динамическая вязкость жидкости; A p — разность давлений на торцах капилляра.

Для кругового цилиндрического капилляра (2) приобретает простой вид:

I s = na ²           .                   (2а)

ηl

Объемный ток I_V , вызванный потенциалом течения, равен [8, с. 183]

^ V S

I V = ^Aa ^ ’                       (3)

где σ — удельная электропроводность раствора в капилляре.

Для положительно заряженного капилляра I V >  0, I s <  0, A v s >  0 и, как и должно быть, положительный знак потенциала течения совпадает с положительным знаком электрокинетического потенциала (положительные знаки потенциалов ДЭС для положительно заряженной поверхности следуют из решения уравнения Пуассона – Больцмана при стандартных граничных условиях, состоящих в том, что потенциал на границе раздела фаз это ψ ₀ , а на бесконечном удалении от поверхности потенциал равен 0). Соответственно, для отрицательно заряженного капилляра I s >  0, I V <  0, A v s <  0 и Z <  0.

Из уравнений (2), (3) и условия стационарности ( I s + I V = 0) обычно получают приводимое в литературе уравнение Гельмгольца – Смолуховского для потенциала течения (см. [4, с. 66]; [7, с. 10]; [8, с. 184] и др.):

^A V s = ее 0 ^Z A p    п^ "

Здесь σ — удельная электропроводность, состоящая из поверхностной проводимости, обусловленной наличием ДЭС, и объемной проводимости жидкости в капиллярной системе. Из последнего выражения получают выражение для электрокинетического потенциала:

Z = П^ ^A V s ее ₀ A p

.

В том случае, когда влиянием ионов ДЭС на электропроводность раствора в капилляре (поверхностной проводимостью) можно пренебречь, иногда записывают уравнение Гельмгольца – Смолуховского в следующем виде:

Z 0 = п^ у ^A V s ее ₀ А p

(5а)

где σ _V — удельная электропроводность свободного раствора, с которым капилляр находится в рав- 0

новесии, а ζ — электрокинетический потенциал, найденный без учета влияния поверхностной проводимости.

Причиной поверхностной проводимости является отличие состава электролита в заряженном капилляре от состава свободного раствора. Свободный раствор электролита электронейтрален, раствор в капилляре имеет суммарный заряд, равный по модулю суммарному заряду стенок капилляра, причем общее количество ионов в единице объема раствора в заряженном капилляре всегда больше, чем в свободном растворе. Если рассматривать простейший случай — индифферентный электролит, то взаимодействие ионов с заряженной поверхностью считается только кулоновским, и распределение ионов в ДЭС описывается обычным уравнением Больцмана [9, с. 95]:

с - ⁽ x ) = c 0, i exp( ^- zF v ( x ) / RT ).              (6)

Здесь с_i ( x ) — распределение концентрации ионов i -го типа; z_i — их валентность; F — число Фарадея; R — газовая постоянная; T — абсолютная температура; ψ ( x ) — распределение электрического потенциала (ось x нормальна поверхности границы твердого тела и раствора и направлена вглубь раствора).

Тогда для симметричного электролита при V(x) * 0 из (6) следует c+ (x) + c- (x) =

= c ₀[exp( - z ₊ Fv ( x ) / RT ) + exp( z - Fv( x ) / RT )] =

= 2 c ₀ ch( zFv ( x ) / RT ) >  2 c ₀.                      (7)

Удельная электропроводность свободного раствора может быть записана следующим образом:

^ v = E ^z 2 cu- ,                     ⁽⁸⁾

( i )

где u_i — подвижность иона (Ом^–1см²моль^–1).

Для раствора в порах можно записать (пренебрегая конвективным вкладом в электропроводность):

^ = E ^zi c^_t^ i ,                        ⁽⁹⁾

где E i , й, — средние по объему капилляра концентрации и подвижности ионов. Если средняя подвижность ионов в капилляре близка к таковой в свободном растворе, то электропроводность раствора в капилляре должна быть выше, чем в свободном растворе. Такой рост удельной

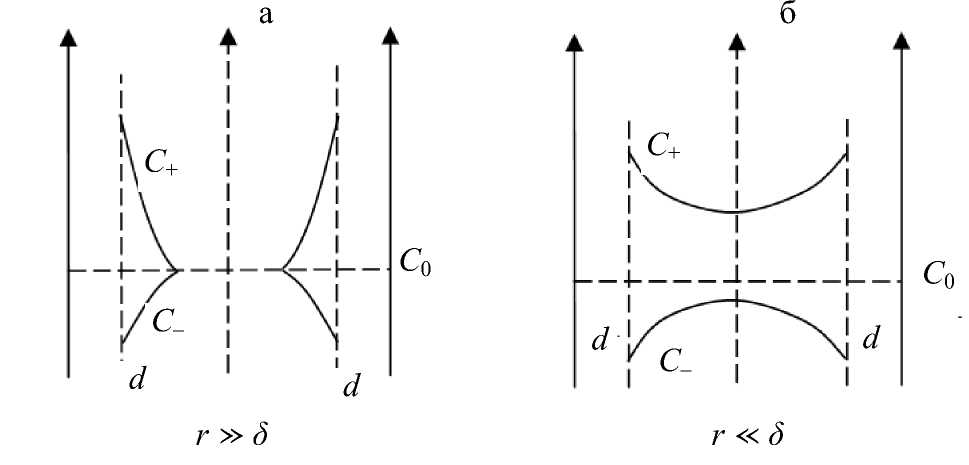
Рис. 6. Схема распределения концентраций противо- и коионов в отрицательно заряженном капилляре.

а — широкий капилляр, не перекрытые ДЭС; б — высокая степень перекрывания ДЭС

электропроводности за счет избыточных ионов ДЭС и называют поверхностной проводимостью.

Из схемы, приведенной на рис. 6, понятно, что чем шире капилляр по сравнению с толщиной диффузного слоя, тем меньше влияние ионов ДЭС на электропроводность и тем она ближе к величине электропроводности внешнего равновесного раствора. При теоретическом описании поверхностной проводимости используют два способа. Первый, предложенный в работах кафедры коллоидной химии ЛГУ [6, 11], предполагает использование следующего уравнения, пригодного для любой капиллярно-пористой системы:

о = о , + O s ,                (10)

где σ _s — поверхностная проводимость, усредненная по всему объему порового канала, которая будет зависеть от электрокинетического радиуса и, следовательно, при постоянной геометрии поры, от толщины диффузного слоя, т.е. от концентрации внешнего раствора электролита. Был также предложен параметр, равный соотношению электропроводностей раствора в капилляре и внешнего равновесного раствора, названный коэффициентом эффективности:

a = о I o _V,                 (11)

величина α стремится к 1 с увеличением размера пор и ростом концентрации электролита.

Второй способ описания поверхностной проводимости — с использованием понятия удельной поверхностной проводимости K_s (избыточная электропроводность ионов ДЭС над 1 см² заряженной поверхности) требует знания геометрии системы [4–7]. Так, например, для цилиндрического капилляра

Os " VOK      aa

Ks =       = °s^ = (a - 1)°V 3,

Aпбк       22

где V ок — объем капилляра, А пбк — площадь боковой поверхности капилляра.

В современной англоязычной литературе при описании влияния поверхностной проводимости на характеристики границы раздела фаз используют параметр Du , который представляет собой безразмерную величину, характеризующую вклад поверхностной проводимости в различные элек-трокинетические и электроакустические эффекты (назван в честь С.С. Духина) [5]:

Du = K_S I a o _V = ( a - 1)/2.         (13)

Если анализировать уравнения типа (5), которые связывают электрокинетический потенциал с измеряемыми величинами электрокинетических параметров, в нашем случае с величиной потенциала течения, или с величинами скорости электроосмоса, электрофоретической подвижности частиц и т.п., то создается впечатление, что элек-трокинетический потенциал зависит от соответствующего электрокинетического параметра. Но электрокинетический потенциал — это равновесная характеристика конкретной границы раздела фаз, зависящая только от их химического состава. Поэтому те электрокинетические параметры, которые мы измеряем (потенциалы и токи течения, скорость электроосмоса и т.д.), зависят от величины электрокинетического потенциала и других параметров системы, связанных с ее структурой, т.е. с поверхностной проводимостью и степенью перекрывания ДЭС. В этом смысле более строго записывать уравнение для потенциала течения в следующем виде:

Δψ           εε

^s = f ( a κ , ζ , β ^*) ⁰ ζ , Δ p           ησ

где f ( a κ , ζ , β ^*) ≤ 1 — функция, учитывающая влияние перекрывания ДЭС на величину потенциала течения, β ^* — параметр, включающий свойства конкретного электролита [5, 12].

Поскольку условием стационарности в режиме потенциала течения является равенство по абсолютной величине направленных в противоположные стороны поверхностного тока Is и объемного тока IV , то в конкретных условиях возникает такой потенциал течения, который обеспечивает это равенство. При высоких степенях перекрывания ДЭС концентрация коионов в поровом канале, от которой в первую очередь и зависят возникающие при наложении внешнего давления токи, может быть на несколько порядков меньше, чем концентрация противоионов (рис. 6), что приводит к уменьшению электрических токов и, следовательно, измеряемых величин Δψs . Эта ситуация в нанопористых слабозаряженных системах наблюдается при концентрациях С < 0.001 М и согласуется с результатами определения чисел переноса ионов в порах — число переноса противоиона становится практически равным единице. Снижение величин потенциалов течения в условиях перекрывания ДЭС и учитывается функцией f (aκ,ζ,β*), которая уменьшается при стремлении aκ к нулю [12].

Уравнение, которое обычно используют для расчета ζ- потенциала в общем случае, записывают, обращая уравнение (14):

ζ ₌ Δ ψ _s      ησ _.

Δ p f ( aκ , ζ , β ^*) εε ₀ ^.

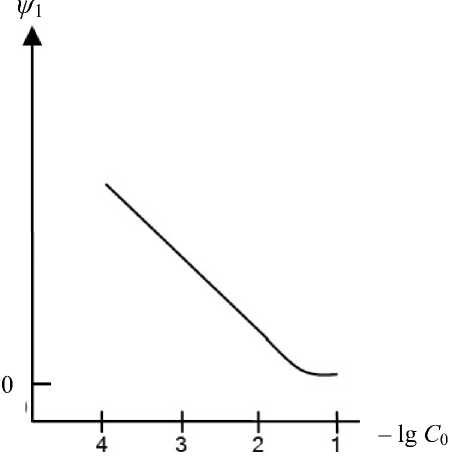
Рис. 7. Зависимость ψ 1 -потенциала от концентрации индифферентного электролита

Если для данной границы раздела фаз величина ζ- потенциала это конкретный численный параметр, то понятно, что, например, при сужении капилляра, которое приведет к росту поверхностной проводимости, т.е. величины α , измеряемая величина Δ ψ _s должна уменьшиться, чтобы электро-кинетический потенциал остался прежним. Чем больше степень перекрывания ДЭС (чем меньше электрокинетический радиус aκ ), тем меньше величина f ( a κ , ζ , β ^*), тем, следовательно, меньше измеряемая величина Δ ψ _s .

Если величины ζ- потенциала рассчитаны правильно, то характер их зависимости от концентрации индифферентного электролита должен быть таким же, какой предсказывается теориями ДЭС для концентрационной зависимости ψ ₁-потен-циалов (рис. 7) — линейная зависимость от log С при больших потенциалах, т.е. в области разбавленных растворов, и зависимость от С ^1/2 при малых потенциалах, т.е. в области растворов более концентрированных (для слабозаряженных систем обычно этот переход типа зависимостей в растворах 1:1 электролитов наблюдается при 0.01 М <  < С < 0.1 М).

На рис. 8 приведен пример расчета электроки-нетического потенциала из величин потенциалов

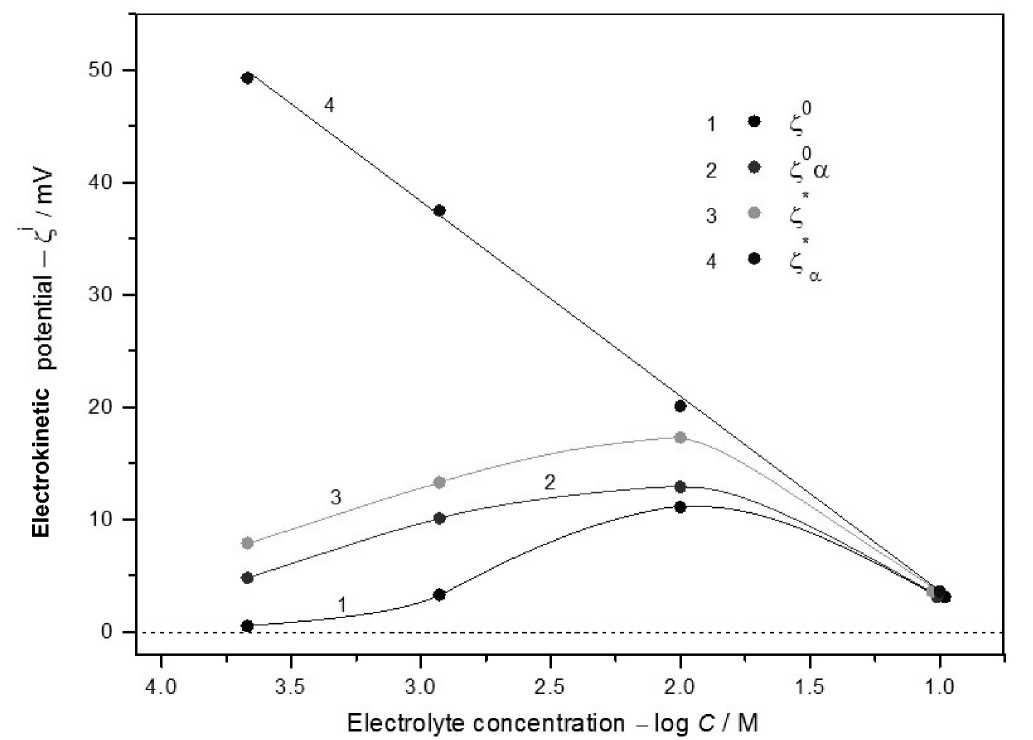
Рис. 8. И з [13]: зависим ос ти эл ектрок и не т иче с кого по т е нц и ала м е м б ран ы из порис т ого с т ек ла в ра с творах KNO 3 , ра с с чит ан н ые по различн ым урав не ни я м.

Расчет: 1 — по ура в н е ни ю (5а); 2 — по уравнению (5), с = o V a; 3 — п о ура в нению (15) , при расче т е фу н кции f и с польз ов ал и эле к тро п ровод нос ть объе м ного ра с твора σ _V ; 4 — п о урав н ен ию (15), при р асчете функции f и с пользов а ли электропровод нос ть ра ств о ра в п о рах σ

тече н ия для по ри стой сте к л ян н ой мем б ран ы , изготовле н ной из н а три е во б оро с или к атног о стекла, со сред н и м ра ди у сом пор 16 н м [13 , ри с. 15, с. 100]. В идн о , что тол ь к о у че т как п ов е рх н остной проводи мос ти, та к и пере к ры в ания Д ЭС п озв о л я ет получить с ог лас у ющу ю ся с те орие й зави с имос т ь Z ( log С ) .

Конечно, при переходе от нанодисперсных систем к микрофильтрам с размерами поровых каналов порядка 1 мкм проблемы, связанные с необходимостью учета перекрывания ДЭС, перестают быть актуальными, но, как правило, в разбавленных растворах необходимо проверять соотношение удельных электропроводностей порового и внешнего раствора. Кроме того, при проведении измерений на реальных промышленных образцах необходимо понимать, насколько изотропны мембраны, т.е. насколько структура мембраны остается постоянной по толщине.

ВЫВОДЫ

В работе приведены особенности протекания процессов, характеризуемых потенциалом течения в электролите, в аспекте реализации жидкостного акустоэлектрического преобразователя. Рассмотрена электрохимия потенциала течения в электролитах. Кроме того, отмечена особенность процесса в растворах электролитов, связанная с влиянием ионной силы электролита, и его зависимость от электрокинетического радиуса. Показано также, что при малых величинах электрокинетического радиуса возникает эффект перекрытия двойных электрических слоев, ведущий к резкому уменьшению абсолютных величин потенциала течения.

Работа выполнена в ИАП РАН в рамках Государственного задания 075-00761-22-00 Министерства науки и высшего образования.