Реализация алгоритма Гейла-Шепли для автоматизации приема абитуриентов в высшее учебное заведение

С введением приоритетов подачи абитуриентами заявлений на выбранные специальности появилось множество вопросов, связанных с размещением: как правильно выбрать последовательность действий для получения стабильного размещения; будет ли стабильное размещение уникальным; если нет, то чем оно отличается от других; можно ли производить зачисление сразу после подачи заявления абитуриентом.

Под стабильным размещением подразумевается ситуация, когда в результате работы алгоритма не найдется та-

ких сочетаний «специальность – абитуриент», которые не образовали пары, а при образовании пары окажутся в более выгодном положении (с точки зрения приоритетов), чем раньше. Другими словами, специальность для абитуриента более предпочтительна, как и абитуриент для специальности при оценке «удачности» сочетаний пар [1].

В качестве основы был выбран алгоритм Гейла-Шепли, поскольку он обеспечивает стабильные размещения, а также зарекомендовал себя в решении подобных задач (например, в системе распределения донорских орга-

нов между больными, модели работы двусторонних рынков и зачислении учащихся в школы [1–5]).

Стоит заметить, что данный алгоритм рассматривает варианты стабильных размещений, которые отличаются сторонами инициации и, следовательно, в результате работы получается набор из двух стабильных размещений, наиболее выгодных для инициирующих сторон [4].

Результаты исследования

Для моделирования работы алгоритма предположим, что:

– абитуриент имеет список приоритетов специальностей, на которые хочет поступить, а также перечень экзаменов и баллов по ним;

– университет имеет список специальностей, каждая из которых обладает квотой на зачисление абитуриентов, а также список экзаменов, необходимых для поступления;

– согласно Федеральному закону об образовании, абитуриенты с одинаковыми баллами зачисляются сверх квоты, если при отказе абитуриентам с наименьшим количеством баллов у специальности остались свободные места.

На рис. 1 представлена схема алгоритма с предлагающей стороной аби-

туриентов; на рис. 2 – с предлагающей стороной специальностей. Стоит заметить, что асимптотика данных алгоритмов будет следующей:

• 1)    с предлагающей стороной абитуриентов: n∙k, где n – количество абитуриентов; k – количество приоритетов у абитуриента;

• 2)    с предлагающей стороной специальностей: m∙p, где m – количество специальностей; p – количество приоритетов у специальности.

Заметим, что такая характеристика получается при условии, что вспомогательные операции (добавление или, удаление абитуриента из размещения и др.) выполняются за константное время.

Для анализа представленных алгоритмов был написан программный код, позволяющий генерировать различные данные о специальностях и абитуриентах, а также тестировать с этими данными предложенные алгоритмы и анализировать полученные результаты [6–10].

С помощью генератора был получен набор данных, который демонстрирует, что размещения различаются не только качественно, но и количественно; квота специальностей следующая: Spec_1 – 2; Spec_ 2 – 3; Spec_3 – 1 (табл. 1–5)

Т а б л и ц а 1

T a b l e 1

Предметы, необходимые для поступления на специальности

Items needed for admission to the specialty

Spec_1	Mathematics	Informatics
Spec_2	Physics	Language
Spec_3	Mathematics	Physics

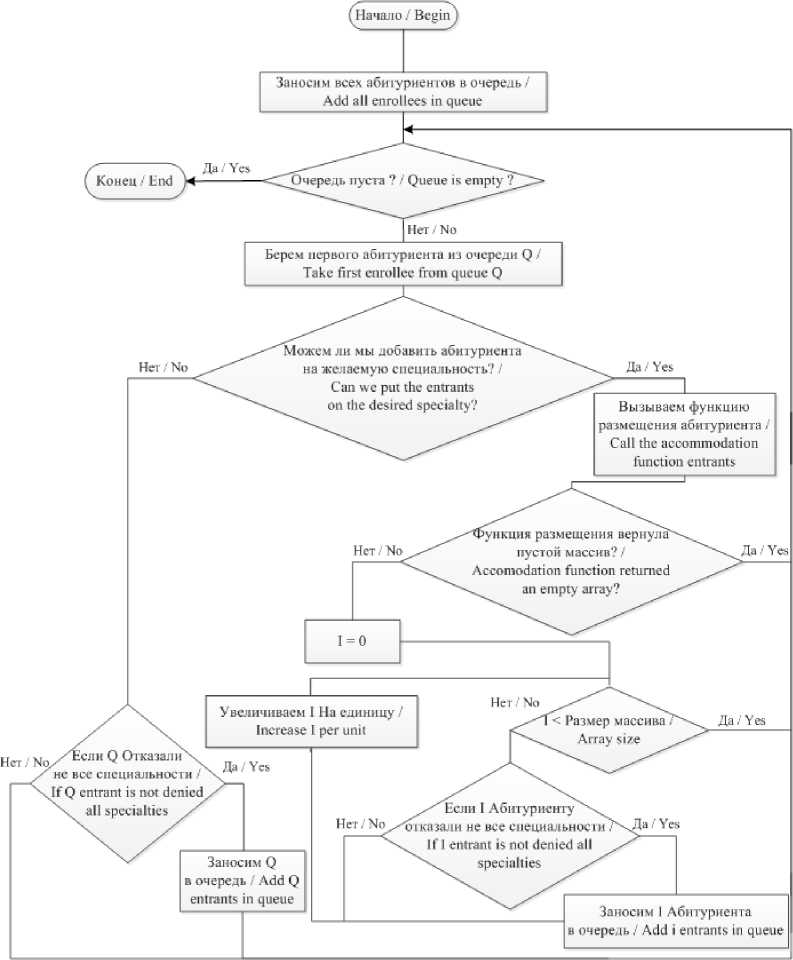
Р и с. 1. Алгоритм действий с предлагающей стороной абитуриентов

F i g. 1. Action algorithm with offering enrollees

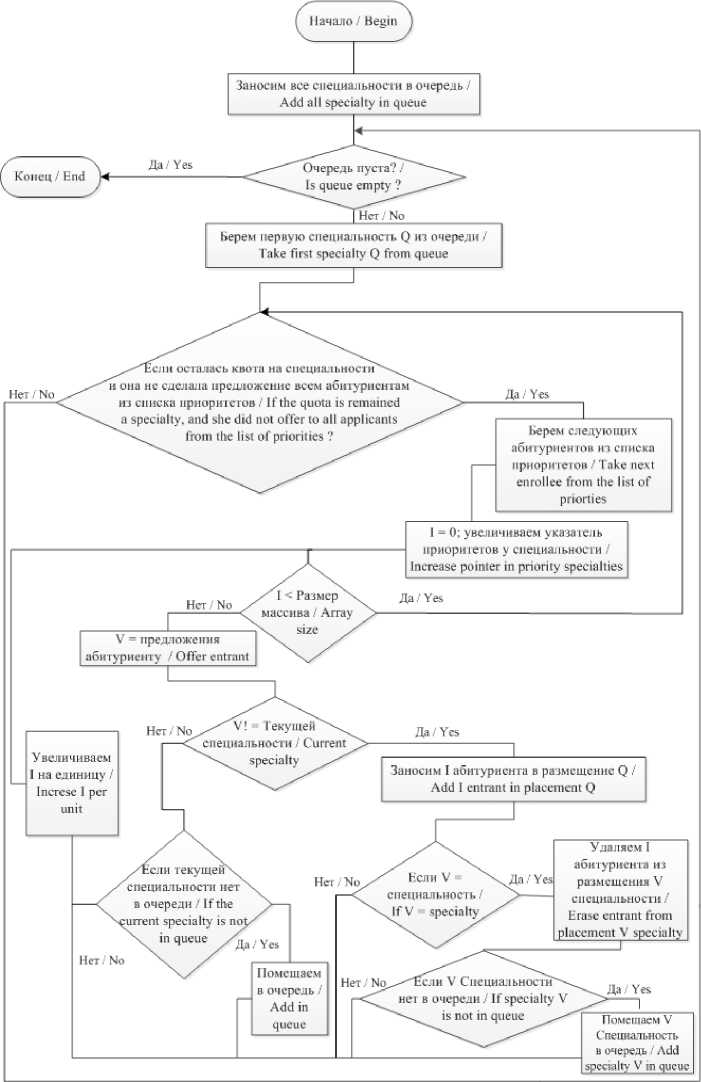
Р и с. 2. Алгоритм действий с предлагающей стороной специальностей

F i g. 2. Action algorithm with offering specialties

Т а б л и ц а 2

T a b l e 2

Экзамены, которые сдали абитуриенты The examinations which passed enrollees

Enrolle_1	Informatics 52	Language 22	Mathematics 7	Physics 3
Enrolle_2	Informatics 97	Language 10	Mathematics 9	Physics 75
Enrolle_3	Informatics 26	Language 86	Mathematics 33	Physics 57
Enrolle_4	Mathematics 53	Physics 42	–	–
Enrolle_5	Informatics 14	Language 3	Mathematics 46	–
Enrolle_6	Informatics 66	Language 11	Mathematics 66	Physics 70
Enrolle_7	Mathematics 72	Physics 100	–	–
Enrolle_8	Language 56	Physics 1	–	–
Enrolle_9	Mathematics 4	Physics 66	–	–
Enrolle_10	Language 50	Physics 36	–	–

Т а б л и ц а 3

T a b l e 3

Приоритеты абитуриентов

The priorities of enrollees

Spec_1	Spec_2	Spec_3
Enrolle_3 59	Enrolle_2 85	Enrolle_7 172
Enrolle_5 60	Enrolle_6 81	–
Enrolle_1 59	Enrolle_10 86	–

Т а б л и ц а 4

T a b l e 4

Распределение с предлагающей стороной абитуриентов

Distribution with offering enrollees

En1	En2	En3	En4	En5	En6	En7	En8	En9	En10
Spec2	Spec2	Spec1	Spec3	Spec1	Spec2	Spec3	Spec2	Spec3	Spec2
Spec1	Spec1	Spec3	–	Spec2	Spec1	–	–	–	–
–	–	Spec2	–	–	–	–	–	–	–

Т а б л и ц а 5

T a b l e 5

Распределение с предлагающей стороной специальностей Distribution with offering specialties

Spec_1	Spec_2	Spec_3
Enrolle_6 132	Enrolle_3 143	Enrolle_7 172
Enrolle_5 60	Enrolle_10 86	–
–	Enrolle_2 85	–

Количественное различие полученных размещений связано с тем, что минимум 2 абитуриента могут оказаться «равными» для одной специальности. Заметим, что если убрать из предложения абитуриента 1 , то размещения будут отличаться только качественно [11].

Качественное различие размещений обусловлено тем, что если для одного абитуриента специальность 1 находится на первом месте в списке приоритетов, это не означает, что для абитуриента 2 она также будет на первом месте. Это справедливо и для специальностей: если абитуриент 1 будет на первом месте в списке приоритетов у специальности 1, это не означает, что он также будет находиться на первом месте у специальности 2, что обусловлено различными критериями оценки абитуриентов для различных специальностей [12–15].

Рассмотрим среднее время работы алгоритма в зависимости от изменения следующих величин:

• 1)    квота на специальности;

• 2)    количество приоритетов у абитуриента;

• 3)    количество специальностей;

• 4)    количество абитуриентов.

• 1)    Среднее время исполнения алгоритмов в зависимости от изменения квоты на специальности (рис. 3–4).

  

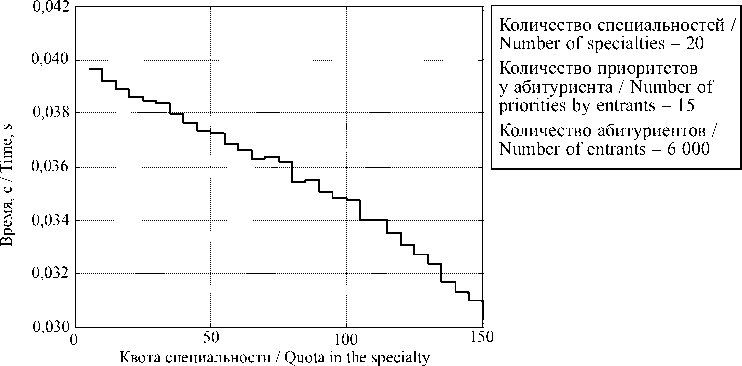
  Р и с. 3. Среднее время исполнения при предлагающей стороне абитуриентов

  F i g. 3. The average time of action when enrollees is offering

  468                                   Информатика, вычислительная техника и управление

  
  
  
  
  

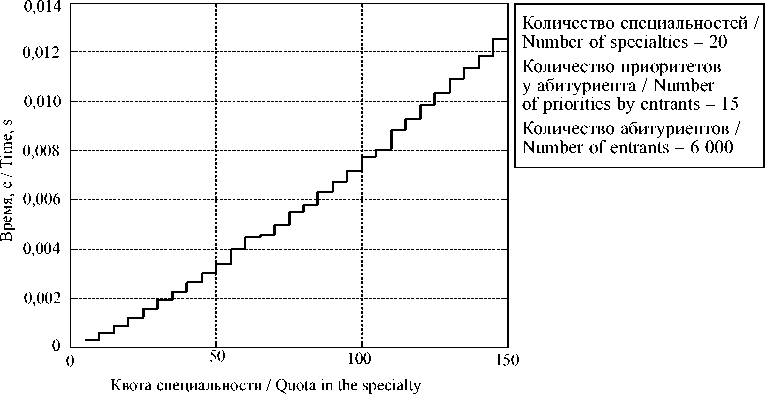
Р и с. 4. Среднее время исполнения при предлагающей стороне специальностей

F i g. 4. The average time of action when offer the specialty

На рис. 3 видно, что при увеличении квоты у специальности среднее время исполнения уменьшается, поскольку абитуриенты получают меньше «отказов». На рис. 4, среднее время увеличивается; это обусловлено тем, что специальности делают больше итераций предложений.

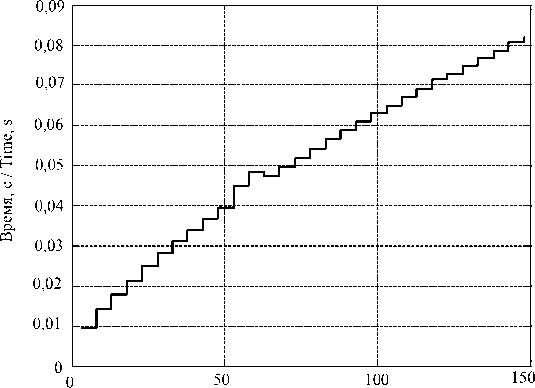
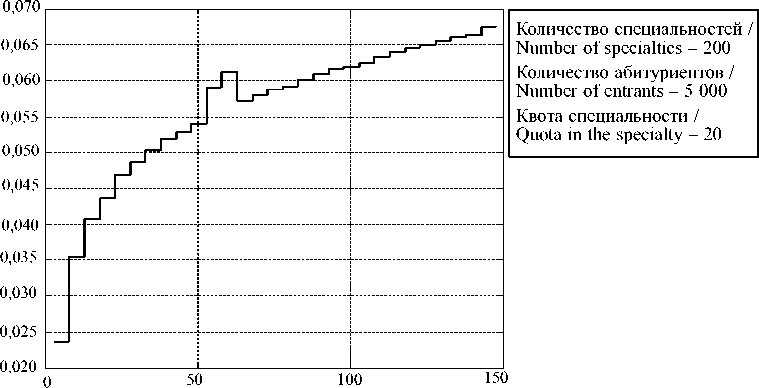
• 2)    Среднее время исполнения алгоритмов в зависимости от изменения количества приоритетов у абитуриента (рис. 5–6).

  

  Количество приоритетов у абитуриента / Number priorities by entrants

  
  

Количество специальностей /

Number of specialties – 200

Количество абитуриентов /

Number of entrants – 5 000

Квота специальности /

Quota in the specialty – 20

Р и с. 5. Среднее время исполнения при предлагающей стороне абитуриентов

F i g. 5. The average time of action when enrollees is offering

Сomputer science, computer engineering and management                                   469

Количество приоритетов у абитуриента / Number priorities by entrants

Р и с. 6. Среднее время исполнения при предлагающей стороне специальностей

F i g. 6. The average time of action when offer the specialty

На рис. 5 показано, что среднее время работы увеличивается, поскольку абитуриенты делают больше предложений. На рис. 6 видно, что время средней работы также увеличивается. Это связано с тем, что при росте количества приоритетов у абитуриента последний чаще получает более выгодные для себя – это увеличивает количество итераций предложения специальностей.

• 3)    Среднее время исполнения в зависимости от изменения количества специальностей (рис. 7–8).

  

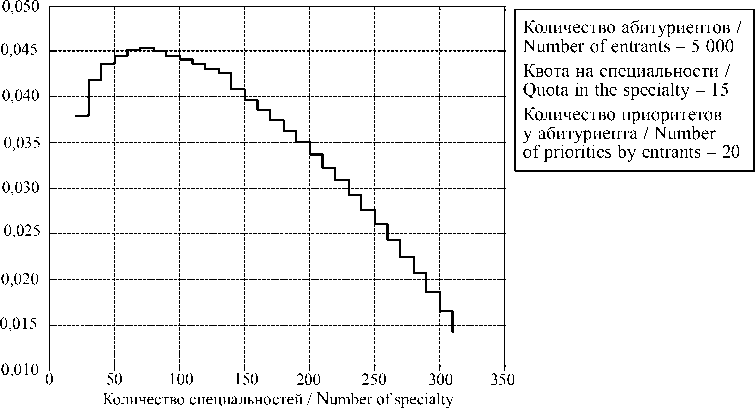
  Р и с. 7. Среднее время исполнения при предлагающей стороне абитуриентов

  F i g. 7. The average time of action when enrollees is offering

  470                                   Информатика, вычислительная техника и управление

  
  
  

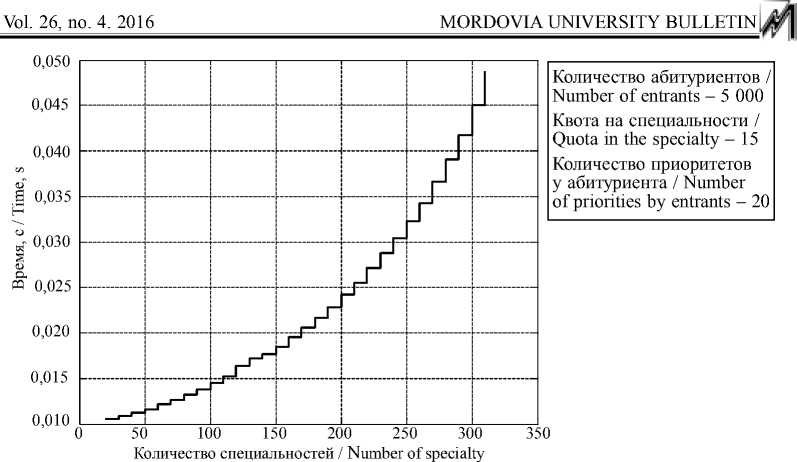
  Р и с. 8. Среднее время исполнения при предлагающей стороне специальностей

  F i g. 8. The average time of action when offer the specialty

  
  

Из рис. 7 видно, что при увеличении количества специальностей среднее время исполнения сначала увеличивается, а затем уменьшается. Увеличение связано с тем, что абитуриенты чаще делают предложения одинаковым специальностям и, следовательно, чаще получают отказ. Уменьшение также связано с тем, что количество специальностей увеличивается и, сле- довательно, абитуриенты чаще делают предложения разным специальностям. На рис. 8 показано, что среднее время исполнения увеличивается при увеличении количества специальностей из-за того, что больше специальностей делают итерации предложения.

• 4)    Среднее время исполнения в зависимости от изменения количества абитуриентов (рис. 9–10).

  

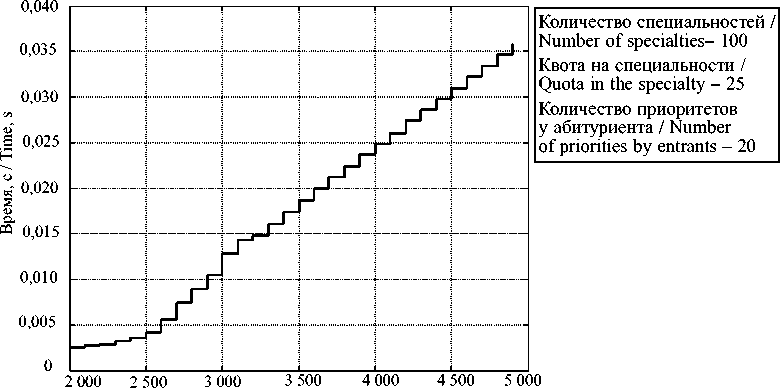
  Количество абитуриентов / Number of entrants

  Р и с. 9. Среднее время исполнения при предлагающей стороне абитуриентов

  F i g. 9. The average time of action when enrollees is offering

  Сomputer science, computer engineering and management                                   471

  
  
  

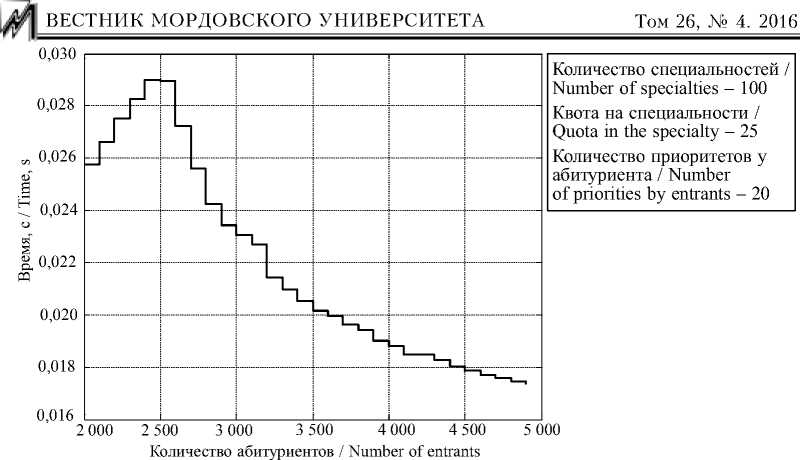
  Р и с. 10. Среднее время исполнения при предлагающей стороне специальностей

  F i g. 10. The average time of action when offer the specialty

  
  

На рис. 9 видно, что среднее время исполнения увеличивается по мере увеличения количества абитуриентов, поскольку количество итераций предложения абитуриентов также увеличивается. Медленный рост временной характеристики обусловлен тем, что на этом отрезке меньше абитуриентов получают «отказ» от специальности, а в дальнейшем – чаще, что увеличивает количество итераций предложения абитуриентов. На рис. 10 показано, что при росте количества абитуриентов сначала среднее время исполнения увеличивается, а затем уменьшается. Увеличение связано с тем, абитуриенты чаще получают более выгодные предложения специальностей, отказывая имеющимся, что увеличиваетколичество итераций предложения специальностями. Уменьшение – с тем, что при дальнейшем увеличении количества абитуриентов у специальностей расширяется «выбор» среди них, из-за чего абитуриенты реже отказывают имеющимся предложениям.

Обсуждение и заключения

В результате работы рассмотренных вариантов алгоритма обеспечивается стабильное зачисление абитуриентов в высшие учебные заведения. В алгоритме с инициирующей стороной «абитуриент» можно производить размещения непосредственно после подачи абитуриентом документов (при изменении или удалении данных придется запустить алгоритм с начала). Для снижения нагрузки на сервер,а также для поддержания актуальной информации о размещении можно запустить алгоритм в отдельном потоке. Данные операции актуальны также для алгоритма с инициирующей стороной «специальность».

Информацию об абитуриентах и размещениях можно хранить в таблицах, чтобы в случае необходимости дубляжа данные остались неизменными.

Поскольку при подаче заявки указывается тип поступления, то при реализации алгоритма можно создавать для каждой специальности несколько таблиц, относящихся к каждому типу поступления.

У приемной комиссии есть множество критериев оценивания одного абитуриента относительно другого, кроме набранных баллов, поэтому рекомендуется использовать функцию, приводящую результат сравнения в соответствие с критериями приема.