Реализация алгоритма нахождения резольвенты матрицы с использованием присоединенной матрицы и характеристического многочлена

Введение. При решении многих задач требуется вычислять резольвенту матрицы [1], не зная ее собственных значений. В частности, такая задача возникает при решении систем линейных алгебраических уравнений с малым параметром методом Ляпунова-Шмидта [2; 3].

В работе [1] приведен подход вычисления резольвенты матрицы с использованием присоединенной матрицы и характеристического многочлена матрицы. Для вычисления последних Д. К. Фаддеевым предложен метод одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы [1].

Изложим алгоритм вычисления резольвенты матрицы на основе подхода, изложенного в [1] и метода Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы.

Алгоритм вычисления резольвенты матрицы. Для вычисления резольвенты постоянной (т х т) —матрицы А

R (Л) = [ЛЕ —А]^-1

воспользуемся формулой [1, с. 112]

R W =

A min ^(/)

где С(Х) - приведенная присоединенная матрица для матрицы [ХЕ — А] (см. [1, с. 99]); Х т1п (А) - минимальный характеристический многочлен матрицы А.

Приведенную присоединенную матрицу С (X) и минимальный характеристический многочлен матрицы А будем вычислять по формулам [1, с. 99-100]

СО) = -^ b_aw

Х т1п^(Х) =

Д(Х) d(X)

где В_А(Х) - присоединенная матрица для матрицы А [1, с. 92], d(X) - наибольший общий делитель всех элементов матрицы В_А(Х),

△ ^(Х) = ^{Х п} - р !^{Х П-1 —} Р 2^{Х П-2}  ----Р п-1^{Х —} Р п >

- характеристический многочлен матрицы А.

Для нахождения присоединенной матрицы ВА(Х) воспользуемся формулой [1, с. 94]

Ва(Х) = В0Хп 1 + В1Хп 2 + В2Хп 3 + ••• + Вп-1, где В0 - единичная (т х т) —матрица, а (т х т) —матрицы Вк ,к = 1,...,п — 1, находятся методом Д. К. Фаддеева по формулам [1, с. 97]

А_к=АВ_к -1 ,

1 Р к = г Sp^, к

Вк = Ак— pkЕ, к = 1, ...,т.

Здесь Е₀ - единичная (т х т) —матрица.

Программная реализация алгоритм вычисления резольвенты матрицы. Приведем фрагменты алгоритма вычисления резольвенты матрицы А на языке Python с использованием пакета SymPy .

Фрагмент кода инициализации матрицы А с целыми случайными элементами а^ , i,j = = 1,^,m из отрезка [-10,10]:

max_aij = 10

Фрагмент кода реализации метода Д. К. Фаддеева одновременного вычисления характеристического многочлена А(Л) и присоединенной матрицы В_А(Л):

def fadeev_method(A):

m = len(A)

B = [0 for i in range(m +1)]

tmpA = [0 for i in range(m +1)]

p = [0 for i in range(m +1)]

for k in range(1, m +1):

tmpA[k] = A * B[k -1]

p[k] = 1 / k * matrix_trace(tmpA[k])

B[k] = tmpA[k] - p[k] * E deltaLambda = lyamda ** m for i in range(1, m +1):

deltaLambda -= p[i] * lyamda ** (m - i)

for k in range(m):

B_A += B[k] * lyamda ** (m - 1- k)

return B_A, deltaLambda

Фрагмент кода вычисления наибольшего общего делителя всех элементов присоединенной матрицы В_А (Л):

d = B_A[0,0]

for i in range(m):

for j in range(m):

Фрагмент кода вычисления приведенной присоединенной матрицы С (Л), минимального характеристического многочлена X min (Л) и резольвенты R (Л) матрицы А :

C = 1 / d * B_A x_min = deltaLambda.as_expr() / d

R = 1 / x_min * C

Вычислительный эксперимент. Вычисления проводились на ноутбуке с процессором 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz и операционной системой Windows 11 Pro.

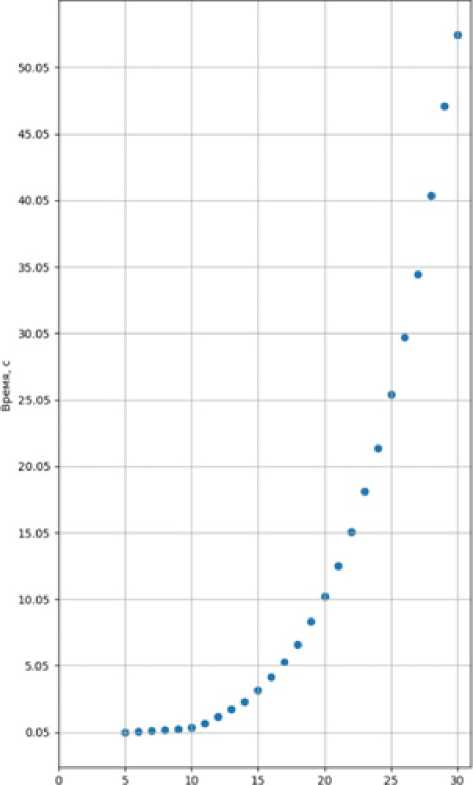
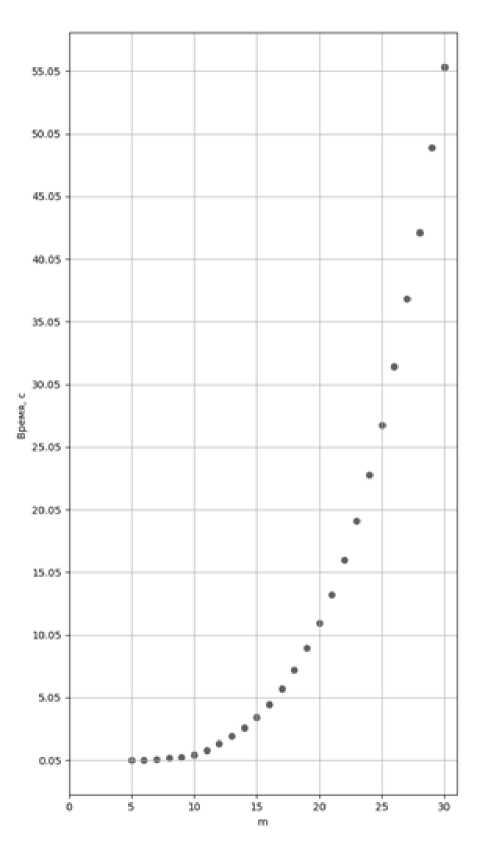
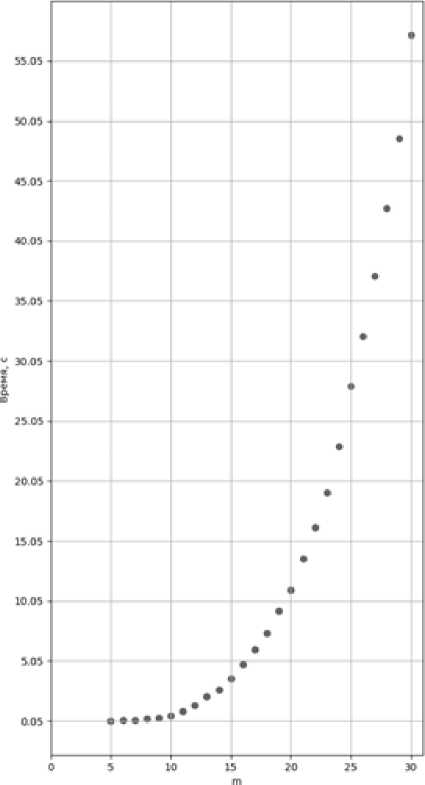
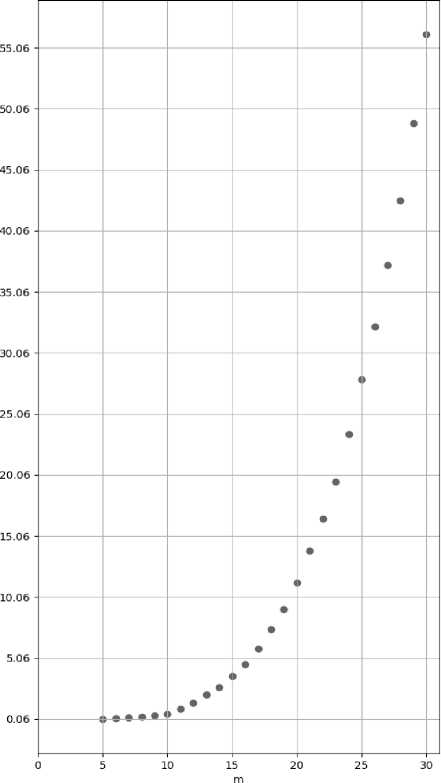
На графиках представлены зависимости скорости работы алгоритма вычисления резольвенты матрицы А с целыми случайными элементами при различных размерностях матрицы.

a )

b )

c )                                                     d )

Рисунок. Графики зависимостей скорости работы алгоритма от размерности матрицы А при условиях: a ) \a ij \ < 10, b ) \a ij \ < 10⁵, c ) \пц\ < 10⁶, d) |%'| < 10⁷, i,j = 1, ...,т

Из графиков видно, что при увеличении значений коэффициентов матрицы А по абсолютной величине скорость работы алгоритма увеличивается незначительно.

Для сравнительного анализа использовалась функция пакета Sympy нахождения обратной матрицы, зависящей от параметра. Вычисления показали, что при т = 30 и \^ ij \ < 10 эта функция уже затрачивает порядка 10 мин., что значительно превышает скорость работы разработанного алгоритма вычисления резольвенты матрицы с использованием приведенной присоединенной матрицы и минимального характеристического многочлена.