Реализация базовых операций для разреженных матриц в контексте решения обобщенной задачи на собственные значения в комплексе ACELAN-COMPOS

УДК 519.688/534–16                                                               Научная статья

Введение. Широкое использование пьезоматериалов в различных отраслях стимулирует изучение их физических характеристик и обусловливает актуальность таких изысканий. В рассматриваемом случае модальный анализ позволяет определить рабочую частоту и коэффициент электромеханической связи пьезоэлементов различных устройств. Эти индикаторы представляют серьезный теоретический и прикладной интерес. Цель исследования — разработка численных методов для решения задачи определения частот резонанса в системе упругих тел. Для достижения цели нужны новые подходы к дискретизации задачи на основе метода конечных элементов и выполнение программной реализации выбранного метода на языке С# на платформе .net. Актуальные решения созданы в контексте библиотеки классов комплекса ACELAN-COMPOS. Основанные на обращении матриц известные методы решения обобщенной задачи на собственные значения неприменимы к матрицам большой размерности. Для преодоления этого ограничения в представленной научной работе реализована логика построения матриц масс и созданы программные интерфейсы для обмена данными о задачах на собственные значения с модулями пре- и постпроцессинга.

Материалы и методы. Для реализации численных методов задействовали платформу .net и язык программирования C#. Валидация результатов исследования проводилась путем сравнения найденных значений с решениями, полученными в известных CAЕ-пакетах (англ. computer-aided engineering — компьютеризированная инженерия). Созданные подпрограммы оценивались с точки зрения производительности и применимости для задач большой размерности. Проводились численные эксперименты с целью валидации новых алгоритмов в задачах малой размерности, которые решаются известными методами в MATLAB. Далее подход тестировали на задачах с большим числом неизвестных и с учетом распараллеливания отдельных операций. Чтобы избежать нахождения обратной матрицы, программно реализовали модифицированный метод Ланцоша. Рассмотрели форматы хранения матриц в оперативной памяти: триплеты, CSR, СSC, SKyline. Для решения системы линейных алгебраических уравнений (СЛАУ) задействовали итерационный симметричный метод LQ, адаптированный к этим форматам хранения.

Результаты исследования . Разработаны новые расчетные модули, интегрированные в библиотеку классов комплекса ACELAN-COMPOS. Проведены расчеты для определения применимости различных форматов хранения разреженных матриц в оперативной памяти и различных методов реализации операций с разреженными матрицами. Графически визуализирована структура матриц жесткости, построенных для одной и той же задачи, но с различной перенумерацией узлов конечноэлементной сетки. Применительно к задаче теории электроупругости обобщены и представлены в виде таблицы данные о времени, необходимом на выполнение базовых операций с матрицами жесткости в различных форматах хранения. Установлено, что перенумерация узлов сетки дает существенный прирост производительности даже без изменения внутренней структуры матрицы в памяти. С учетом поставленных задач исследования названы преимущества и слабые стороны известных форматов хранения матриц. Так, CSR оптимален при умножении матрицы на вектор, SKS — при обращении матрицы. В задачах с числом неизвестных порядка 10³ выигрывают в скорости итерационные методы решения обобщенной задачи на собственные значения. Оценивалась производительность программной реализации метода Ланцоша. Измерялся вклад всех операций в общее время решения. Выяснилось, что операция решения СЛАУ

Механика

занимает до 95 % от общего времени работы алгоритма. При решении СЛАУ симметричным методом LQ наибольшие вычислительные затраты нужны для умножения матрицы на вектор. Для увеличения производительности алгоритма прибегли к распараллеливанию с общей памятью. При использовании восьми потоков производительность выросла на 40–50 %.

Обсуждение и заключение . Полученные в рамках научной работы программные модули были внедрены в пакет ACELAN-COMPOS. Оценена их производительность для модельных задач с квазирегулярными конечноэлементными сетками. С учетом особенностей структур матриц жесткости и масс, получаемых при решении обобщенной задачи на собственные значения для электроупругого тела, определены предпочтительные методы для их обработки.

Original article

Implementation of Basic Operations for Sparse Matrices when Solving a GeneralizedEigenvalue Problem in the ACELAN-COMPOS Complex

Pavel A. Oganesyan M, Olga O. Shtein

Southern Federal University, Rostov-on-Don, Russian Federation

Introduction. The widespread use of piezoelectric materials in various industries stimulates the study of their physical characteristics and determines the urgency of such research. In this case, modal analysis makes it possible to determine the operating frequency and the coefficient of electromechanical coupling of piezoelectric elements of various devices. These indicators are of serious theoretical and applied interest. The study was aimed at the development of numerical methods for solving the problem of determining resonance frequencies in a system of elastic bodies. To achieve this goal, we needed new approaches to the discretization of the problem based on the finite element method and the execution of the software implementation of the selected method in C# on the .net platform. Current solutions were created in the context of the ACELAN-COMPOS class library. The known methods of solving the generalized eigenvalue problem based on matrix inversion are not applicable to large-dimensional matrices. To overcome this limitation, the presented scientific work implemented the logic of constructing mass matrices and created software interfaces for exchanging data on eigenvalue problems with pre- and postprocessing modules.

Materials and Methods. A platform was used to implement numerical methods .net and the C# programming language. Validation of the research results was carried out through comparing the values found with solutions obtained in well-known SAE packages (computer-aided engineering). The created routines were evaluated in terms of performance and applicability for large-scale tasks. Numerical experiments were carried out to validate new algorithms in smalldimensional problems that were solved by known methods in MATLAB. Next, the approach was tested on tasks with a large number of unknowns and taking into account the parallelization of individual operations. To avoid finding the inverse matrix, a modified Lanczos method was programmatically implemented. We examined the formats for storing matrices in RAM: triplets, CSR, СSC, Skyline. To solve a system of linear algebraic equations (SLAE), an iterative symmetric LQ method adapted to these storage formats was used.

Results. New calculation modules integrated into the class library of the ACELAN-COMPOS complex were developed. Calculations were carried out to determine the applicability of various formats for storing sparse matrices in RAM and various methods for implementing operations with sparse matrices. The structure of stiffness matrices constructed for the same task, but with different renumbering of nodes of a finite element grid, was graphically visualized. In relation to the problem of the theory of electroelasticity, data on the time required to perform basic operations with stiffness matrices in various storage formats were summarized and presented in the form of a table. It has been established that the renumbering of grid nodes gives a significant increase in performance even without changing the internal structure of the matrix in memory. Taking into account the objectives of the study, the advantages and weaknesses of known matrix storage formats were named. Thus, CSR was optimal when multiplying a matrix by a vector, SKS was optimal when inverting a matrix. In problems with the number of unknowns of the order of 103, iterative methods for solving a generalized eigenvalue problem won in speed. The performance of the software implementation of the Lanczos method was evaluated. The contribution of all operations to the total solution time was measured. It has been found that the operation of solving SLAE takes up to 95% of the total time of the algorithm. When solving the SLAE by symmetric LQ method, the greatest computational costs were needed to multiply the matrix by a vector. To increase the performance of the algorithm, parallelization with shared memory was resorted to. When using eight threads, the performance gain increased by 40– 50%.

Discussion and Conclusion. The software modules obtained as part of the scientific work were implemented in the ACELAN-COMPOS package. Their performance for model problems with quasi-regular finite element grids was estimated. Taking into account the features of the structures of the stiffness and mass matrices obtained through solving the generalized eigenvalue problem for an electroelastic body, the preferred methods for their processing were determined.

Введение. Устройства из пьезоматериалов широко используются, давно активно изучаются и совершенствуются. Отдельно следует отметить медицинские ультразвуковые приборы (оборудование для диагностики, ультразвуковые скальпели) [1–4] и мобильные генераторы энергии [5]. Исследование [6] описывает комбинирование фото- и пьезоэлектрического эффектов для создания действенных компактных источников энергии. В науке и промышленности изучаются новые материалы, рассчитанные на эксплуатацию в специфических условиях. В [7] рассматривается создание бессвинцового пьезоактивного состава, подходящего для эксплуатации при различных температурах.

В исследовании пьезоэлементов важную роль играет этап модального анализа, позволяющий установить частоты резонанса и антирезонанса устройства. Эти данные:

– необходимы для выяснения рабочей частоты устройства;

– позволяют определить коэффициент электромеханической связи — важный индикатор эффективности устройства;

– являются входной информацией в численных экспериментах для задач на вынужденные колебания.

Цель исследования — создание численных методов решения задачи определения частот резонанса для системы упругих тел. Достижение заявленной цели требует решения двух задач. Первая: разработать методы дискретизации задачи на основе метода конечных элементов (МКЭ). Вторая: провести программную реализацию выбранного метода на языке С# на платформе .net. Все известные программы учитывают контекст библиотеки классов комплекса ACELAN-COMPOS [8]. При решении обобщенной задачи на собственные значения широко применяются методы, основанные на обращении матриц. Однако они неприменимы к матрицам большой размерности. В представленной научной работе это ограничение преодолевается следующим образом:

– дополнительно реализована логика построения матриц масс;

– созданы программные интерфейсы для обмена данными о задачах на собственные значения с модулями преи постпроцессинга.

Материалы и методы. В первую очередь предлагаемый подход призван решать статические задачи электроупругости при реализации метода осреднения [9], который задействуют для расчета эффективных свойств пьезокомпозитов. В связи с этим на этапе построения глобальных матриц МКЭ представлены только матрицы жесткости. В данном исследовании дополнительно реализовали логику построения матриц масс и разработали программные интерфейсы (application programming interface, API, англ. — интерфейс прикладного программирования) для обмена данными о задачах на собственные значения с модулями пре- и постпроцессинга. Разработанные подпрограммы оценивались с точки зрения производительности и применимости для задач

Механика

большой размерности. Проводились численные эксперименты с целью валидации созданных алгоритмов для таких задач малой размерности, которые позволяют получить решение общими методами в вычислительном пакете MATLAB. Далее выполнялось тестирование на задачах с большим числом неизвестных и с учетом распараллеливания отдельных операций.

Математическая модель решаемой задачи состоит из определяющих соотношений [9]:

Р™®2u + а8фрфitou-У-П = фф V-D = 0 ,(1)

,

Q = cE - (е + р5ф8) - eTj - E , D + g^D = ey - (e + gd8) + э/ - E,

8 = (Vu + VuT) / 2 ,E = -Vф.(3)

Здесь ст — тензор напряжений; p j — плотность тела; e — тензор деформаций; и — вектор перемещений; D — вектор электрической индукции; E — вектор напряженности электрического поля; f_j — вектор массовых сил; ф — электрический потенциал; a dj , в dj , S d — коэффициенты демпфирования; c E , e T , 3^s j — тензоры упругих констант, пьезомодулей и диэлектрических проницаемостей; индекс j — номер тела в модели.

Дискретизация выполняется заменой:

и (x, t ) = N T ( x ) - U(t) , ф ( x, t ) = N^T ( x ) - Ф ( t ) .

Здесь N u — матрица функций формы для поля перемещений; N ϕ — вектор функций формы для электрического потенциала; U ( t ) , Ф ( t ) — глобальные векторы соответствующих узловых степеней свободы.

В таком случае исходная задача (1–3) приобретает вид:

M - a + K - a = F .                                            (4)

Здесь матрицы M и K являются глобальными матрицами масс и жесткости соответственно, а вектор a представляет собой общий вектор неизвестных:

a = [ U , Ф].

В задаче теории электроупругости:

М = 1 Mu u  0| KKuu ^Ku u   ^{Ku ф} I

M ⁽ 0 о ) ,       ( k T ф   - к фф ) .                                        ⁽⁵⁾

Матрицы M_uu , K_uu и K _фф — симметричные. В случае гармонических колебаний на собственной частоте m i можно записать:

a = v i sin(to i t ), обозначив через v i соответствующий собственный вектор.

Рассмотрим свободные колебания если F = 0 . В этом случае задача (4) представляется в виде:

-to ? Mv i + K - V i = 0.                                               (6)

Таким образом, исходная задача сводится к обобщенной задаче на собственные значения (6). Для ненулевого v i неравенство (6) решается нахождением матрицы, обратной K . Однако при этом разреженная матрица становится заполненной, то есть метод непригоден для матриц больших размеров. Поэтому нужно использовать другие методы, не требующие нахождения обратной матрицы. Для решения этой задачи в данной работе программно реализован модифицированный метод Ланцоша [10]. Автор этой модификации — Т.С. Мартынова. Описание разработки в данной статье не приводится. Из используемых в методе операций наиболее затратной с точки зрения вычислительных ресурсов оказалось решение системы линейных алгебраических уравнений (СЛАУ), необходимое для выполнения спектральной трансформации.

Матрицы M и K — разреженные, с небольшим числом ненулевых элементов. Для хранения таких матриц в оперативной памяти используются несколько форматов:

– триплеты или координатный формат;

• –    CSR (англ. compressed sparse row — сжатый разреженный ряд);

• –    СSC (англ. compressed sparse column — сжатый разреженный столбец);

  – формат хранилища SKyline (англ. SKS — метод).

Координатный формат предполагает хранение троек (триплетов) значений (i, j, k), представляющих собой координаты (i, j) и значения (k) ненулевых элементов. CSR иногда называют CRS или Йельским форматом. Он предполагает хранение разреженной матрицы в виде трех массивов. Рассмотрим матрицу размера N с NZ ненулевыми элементами. Опишем возможную организацию ее хранения. Все ненулевые элементы нужно разместить в одном массиве размера NZ . Позиции этих элементов в столбцах разместить в другом массиве размера NZ , а третий массив размера N использовать для хранения индексов первых элементов строк. Аналогично реализуется хранение в формате CSC.

Формат SKS предполагает хранение ленты матрицы переменной ширины, включающей в себя все ненулевые элементы. В этом случае допускается хранение нулей. Эффективность этого формата зависит от перенумерации строк матрицы. Методы сокращения размера ленты описаны в [11], однако требует отдельного исследования их применимость к матрице жесткости, получаемой при решении трехмерной задачи с использованием МКЭ.

Для решения СЛАУ задействовали итерационный симметричный метод LQ (Symmetric LQ Method, SYMMLQ [12]), адаптированный к перечисленным выше форматам хранения.

Результаты исследования. В начале исследования выбрали оптимальный формат хранения для разреженных матриц. Координатный формат позволяет быстро добавлять и изменять элемент матрицы. Эти операции необходимы на этапе сборки глобальной матрицы и при учете граничных условий. Кроме того, для плохо обусловленных матриц, к которым относится K , часто применяют предварительное преобразование для нормирования. Его также удобно выполнять в координатном формате. Однако такой формат неэффективен, если речь идет об алгебраических операциях.

CSR плохо приспособлен для изменения структуры матрицы: добавляя ненулевой элемент, нужно выполнять вставку в два массива. При этом матрица умножается на вектор очень просто и эффективно.

SKS имеет аналогичные проблемы с добавлением ненулевых элементов и сильно зависит от перенумерации неизвестных в задаче. Остановимся на примере квазирегулярной сетки, которая используется в пакете ACELAN-COMPOS для работы с представительными объемами композитов. Ширина ленты, содержащей все ненулевые элементы, может быть определена заранее и зависит от числа узлов и типа конечного элемента. В общем случае произвольной конечноэлементной сетки сложно заранее оценить размер ленты.

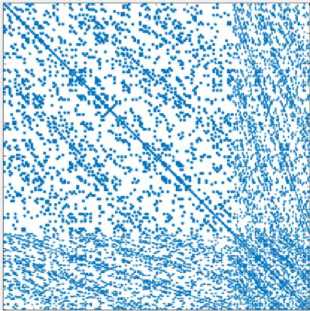
В численных экспериментах использовали четыре способа нумерации неизвестных. На рис. 1 представлена структура матриц жесткости, построенных для одной и той же задачи, но с различной перенумерацией узлов конечноэлементной сетки.

а )

б )

в )

г )

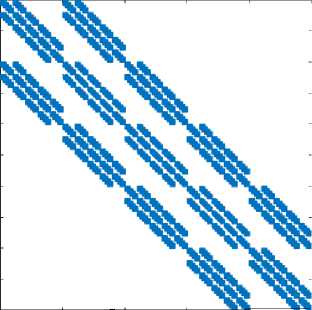
Рис. 1. Структура матриц жесткости при различных методах нумерации узлов: а — неизвестные упорядочены по узлам; б — сначала упорядочены по узлам перемещения, затем потенциалы; в — узлы отсортированы по слоям КЭ-сетки, а неизвестные — по узлам; б, г — узлы отсортированы по слоям КЭ-сетки, а неизвестные — как в примере

Механика

Итак, сетка представляла собой куб с регулярным разбиением восьмиузловыми конечными элементами. Для иллюстраций использовалась модельная матрица из 500 строк. Матрицы, представленные на рис. 1 а и 1 б , не подвергались дополнительной перенумерации узлов и отличаются только нумерацией степеней свободы. В 1 а :

a = [ u 1 x , u 1 y , u 1 z , ^фР'“, u Nx , u Ny , u Nz , ^ф N ] .

В 1 б неизвестные, отвечающие за распределение потенциала, собраны в конце вектора:

a = [ u 1 x ’ ^U 1 y ’ ^U 1 z ’■■; u Nx ’ u Ny ’ u Nz ’ Ф 1 ,"Ч Ф N ^{] .}

Неизвестные в матрицах 1 в и 1 г занумерованы аналогично, но узлы конечноэлементной сетки предварительно перенумерованы согласно их координатам путем поочередной сортировки всех узлов по каждой из координат. Такой прием широко используется для построения более эффективных модулей решения СЛАУ, так как позволяет работать с матрицей в специальном ленточном формате, удобном для распараллеливания. Для комплекса ACELAN-COMPOS реализованы подобные внешние модули [13–15], однако в данной работе использовались только форматы хранения разреженных матриц общего вида.

В таблице 1 сведены данные о времени, необходимом на выполнение базовых операций с матрицами в различных форматах.

Таблица 1

Время для выполнения базовых операций с матрицей жесткости в задаче теории электроупругости.

19 652 строки

Формат хранения	Операция	Затраченное время, мс
		1 а	1 б	1 в	1 г
CSR	Конвертация из координатного формата	123	132	97	117
CSR	Умножение на вектор, 100 операций	260	260	260	260
SKS	Конвертация из координатного формата	690	703	124	268
SKS	Умножение на вектор, 100 операций	60 558	61 450	7 616	22 113

Результаты экспериментов показали, что операция преобразования из координатного формата хранения в компактные занимает мало времени. При этом перенумерация узлов сетки для формирования блочно-ленточной матрицы позволяет получить заметный прирост производительности даже без изменения внутренней структуры матрицы в памяти. Формат CSR оказался оптимальным с точки зрения эффективности операции умножения матрицы на вектор. При обращении матрицы формат SKS более эффективен, однако для задач с числом неизвестных порядка 103 заметно быстрее работают итерационные методы решения обобщенной задачи на собственные значения.

Далее экспериментально оценили производительность программной реализации метода Ланцоша. Измерили вклад всех операций в общее время решения. В результате установили, что операция решения СЛАУ занимает до 95 % от общего времени работы алгоритма. В ходе работы алгоритма строится подпространство Крылова, и в зависимости от его размерности меняется число СЛАУ, которые необходимо решать. Отметим, что размерность подпространства Крылова выбиралась на основе эвристик относительно числа искомых собственных значений. При этом СЛАУ отличаются только правой частью, благодаря чему требования к выделяемой памяти остаются невысокими. Среди базовых операций, применяемых в ходе решения СЛАУ методом SYMMLQ, наибольшие вычислительные затраты нужны для умножения матрицы на вектор.

Для увеличения производительности алгоритма реализовано простейшее распараллеливание с общей памятью. Для формата CRS выделялись блоки строк. Они передавались в отдельные потоки, которые вычисляли соответствующие компоненты результирующего вектора. Прирост производительности составил 40–50 % при использовании 8 потоков. При этом для матриц порядка 103 элементов прирост был около 40 %, а для матриц порядка 104 — около 50 %.

Обсуждение и заключение. В рамках данной работы реализован метод решения обобщенной задачи на собственные значения для матриц, получаемых при моделировании электроупругих тел. Созданы программные модули на языке C# для построения матриц масс методом конечных элементов и выполнения вспомогательных операций в рамках метода Ланцоша (работа с векторами подпространства Крылова, переортогонализация, нахождение собственных векторов). Вычислительная сложность обусловлена в основном операциями умножения разреженных матриц на вектор. В связи с этим проводились численные эксперименты по определению оптимальных форматов хранения матриц, оптимальной структуры матрицы, получаемой в результате перенумерации узлов КЭ-сетки и степеней свободы в узлах. Разработана версия итерационного алгоритма SYMMLQ с использованием параллельных вычислений. Итоговая схема работы включает три пункта.

Во-первых, строятся глобальные матрицы в координатном формате с алгоритмом перенумерации (рис. 1 в ). Во-вторых, данные преобразуются в формат CRS. В-третьих, данные обрабатываются методом Ланцоша, который включает метод SYMMLQ для решения СЛАУ. Результаты работы включили в программный пакет ACELAN-COMPOS.