Реализация блочного шифра "кузнечик" с использованием векторных инструкций

«Кузнечик» представляет собой блочный шифр с размером блока. 128 бит. Обозначим множество всевозможных двоичных строк длины s как Ks. Алгоритм зашифрования сводится к последовательному применению следующих операций:

• •    Побитовая операция сложения по модулю 2: X [k](a) = к ф a, где к, a Е V128-

• •    Биективное нелинейное преобразование: S(a) = S (ai51|... || ao) = ^(ai5) ||... || ^(ao), где at Е V8, симв олом || обозначена операция конкатенации, ал : V ^ V8   некоторая

известная подстановка.

• •    Линейное преобразование: L : V128 ^ V128.

С учётом этих обозначений функции зашифрования Е (a) и расшифрования D(a) а Е V128, могут бвітв представленві в следующем виде:

Dki,...,k_to (a) = X [ ki ] S ^-1L^-1X к ] ...S ^-1L^-1X №-Ч^-1Х [ k_w ]( a ) ,           (2)

где к1, ... к1о — раундовые ключи. Эти ключи вырабатываются один раз в начале алгоритма, вычисляются также с помощью X-, S-, и L-преобразований и не оказывают существенного влияния на скорость работы шифра, поэтому в рамках статьи алгоритм развёртывания ключа не обсуждается. Здесь и далее раундовые ключи предполагаются уже вычисленными. Линейное преобразование L может быть осуществление с помощью 16 циклов работы РСЛОС (регистра сдвига с линейной обратной связью), показанного на рис. 1. Под умножением подразумевается умножение над полем Галуа по модулю неприводимого многочлена р(ж) = ж⁸ + ж⁷ + ж⁶ + ж + 1, под at подразумеваются байты одного блока.

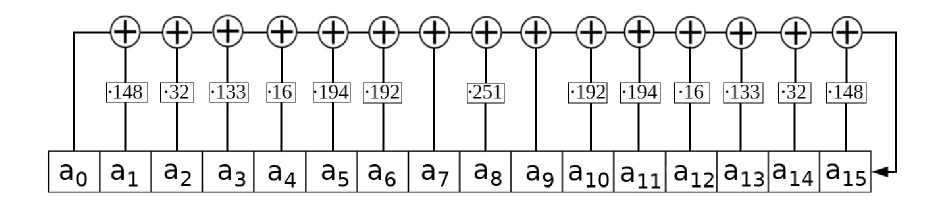
Рис. 1. РСЛОС, реализующий L-преобразоваиие

Такое решение является предпочтительным при аппаратной реализации шифра, однако при создании программной реализации удобнее представить L-преобразование в матричной форме. Результат работы одного такта РСЛОС можно записать в виде

V

ai-1\		/ Ci-1 Ci-2 Ci-3 ... С2   С1 Co \	k	/ ai-Д
ai-2		1   0   0  ... 000		ai-2
a*-3 i i	=	0   1   0  ... 000 •                     .                        .                     .                 .                 .                   •	·	ai-з •
i i a*		•                        •                        •                     •                 •                 •                • 0   0   0  ... 100		• a1
a* )	\ 0      0      0     ...    0    1   0 /		\ ao )

.

/ a^-Д    / С„-1  С„-2  С„-3  ...  С2   С1  Со \ a*-2            1      0      0    ...   0    0    0 a*i-3            0      1      0    ...   0    0    0 • /an-x\ ai-2 an-3 · • •  ••••••• al             0      0      0    ...   1    0    0 \ a0 /    \  0     0     0    ...   0   1   0 / • • a1 \ ao / где a* — новые компоненты вектора. Результат работы после к тактов:

Применение L-преобразования в такой форме существенно быстрее, чем при моделировании РСЛОС. Однако профилирование программы при помощи утилиты callgrind показало, что на L-преобразование приходится приблизительно 75% времени исполнения программы.

2.    Обзор существующих методов

Так как большую часть работы программы занимает L-преобразование, оптимизация операций зашифрования и расшифрования сводится к оптимизации умножения вектора на матрицу в конечном поле. Для ускорения этой операции общепринятым является использование таблиц предвычислений (LUT, Lookup Table).

2.1.    Построение LUT

Особенностям построения таких таблиц уделено должное внимание в [2]. Для полноты изложения кратко приведём рассуждения из указанной статьи. Вычисляется матрица уравнения (3) для случая к = 16. Определим для г-го столбца полученной матрицы отображение L{ (b) : V8 ^ V128 такое, что

Li ( 5 ) = ^Ci,15 • ^b II ^Ci,14 • ^b || . . . || Ci,0 • ^b, ^b E ^V8.

Тогда L-преобразование может быть представлено в виде

L(a) = Li5 ( ai5 ) ф Li4(ai4) ф ... ф Li ( ai ) ф Lo ( ao ) .

LUT имеет размер 16x256, каждый элемент таблицы является блоком данных из 16 байт и строится по следующему принципу: LUT [г][у] есть результат покомпонентого умножения j-го байта исходного вектора на г-й столбец матрицы L-преобразования. Таким образом, для осуществления LS-преобразования над блоком необходимо произвести сложения по модулю 2 всех 16 блоков из LUT.

2.2.    Объединение S- и L-преобразования

Определим теперь преобразование L_i : V8 ^ V128, г = 0 ,..., 15 как

Li ( b ) = Ci,i5 • л ( Ь )|| с і, і4 • л ( Ь )|| ... || с і, о • x(b), b E V8.

Тогда композицию L- и S-преобразований можно представить в виде

LS(а) = Li5(ai5) ф Li4(ai4) ф ... ф Lo(ао), то есть строится таблица предвычислений, по структуре аналогичная предыдущему пункту. Отличие заключается в том, что L- и S-преобразования объединены в одно. Теперь не составляет труда реализовать все три базовые преобразования из (1) как одно LSX-преобразование (enc_ls_table - это LUT):

Листинг 5.1. LSX-преобразование с использованием LUT void Grasshopper :: ApplyLSX ( Block& data, const Blockfe key) {

ApplyX( data , key ) ;

Block tmp{};

for (size_t 1 = 0; i < block_size ; 1ФФ) ApplyX (tmp , enc_ ls_ t able [ i ] [ dat a [ i ] ] ) ;

data = tmp ;

}

• 2.3.    LUT для L-^S -1

Особенности построения LUT для обратного преобразования связаны с тем, что в уравнении (2) преобразование L применяется перед S. Решение этой проблемы может быть найдено в [2]. А именно, преобразуем это уравнение:

D_ki,...,_kio (а) = X [ki]S^-1L^-1X M-S-1L-1X [k9]S^-1L^-1X [к*) =

= X [ki\S -1L-1X к ]...S -1L-1X [k9^S^-1L^-1X [kio\S^-1 S (а). (4)

С учётом линейности L-преобразования

L^-1X №^-1(а) = L^-1 (S^-1(а) Ф к») = L^-1(S^-1(a)) Ф L^-1(k) = L^-1S^-1(a) Ф L^-1 (к») = = X [L^-1 (k»)^L^-1S^-1(а). (5)

Применяя (5) к (4), получим

Dki,...,k_to (а) = X [ki\S^-1L^-1X [k2\...S ^-1L^-1X [k9^S^-1L^-1X [к_w]S^-1S(а) =

= X [k^S^-1(L^-1X[k2]S ^-1)... (L^-1X [kio]S—1)S(а) =

= X[ki]S^-1(X [L^-1(k2]L^-1S^-1) ... (X[L^-1(kio]L^-1S^-1)S (а). (6)

Таким образом, операция зашифрования также может бвітв сведена к объединённому L-1S ^--^-преобразованию, реализованному через LUT (в предположении, что значения L^-1(ki ) заданы). От операции зашифрования операция расшифрования отличается применением дополнительно подстановок S и S^-1, поэтому расшифрование в режимах ЕСВ и СВС будет заведомо медленнее.

2.4.    Использование векторных инструкций

Для дальнейшей оптимизации можно использовать 128-битные хшш регистры, размер которых совпадает с размером блока шифра. Однако дизассемблирование модифицированной таким образом программы показывает, что цикл, отвечающий за применение склеенного LSX-преобразования, содержит дополнительную инструкцию битового сдвига влево:

Листинг 5.2. Часть результата дизассемблирования цикла LSX-преобразования movzbl 0x3(%rsi),           %еах shl     $0x4 ,                    %rax xorps 0x3000 (%rdx ,% rax , 1) , %xmm0

Адрес А в памяти вычисляется по формуле А = В + I*S + D, где В — базовое смещение, I — индекс, S — масштаб (scale), D — смещение (displacement). В приведённом коде rdx содержит базовое смещение В, гах используется для вычисления смещения D. Так как в LUT 16-байтовые векторы хранятся друг за другом, приходится домножать смещение на 16, используя битовый сдвиг, и передавать результат как D. Это смещение нельзя задать, используя S, так как S Е {2,4, 8} (см. [5]). Ещё одна оптимизация заключается в пред-вычислении смещений в начале цикла с тем, чтобы не исполнять в дальнейшем операцию битового сдвига, а передавать в качестве memory operand готовое D. Для предвычисления смещений также используются регистры xmm. Из блока данных посредством операций И и И НЕ с помощью маски выделяются отдельно чётные и нечётные байты. К полученным после применения И и И НЕ блокам применяются операции битового сдвига на 4 вправо (srli) и влево (sill) соответственно (см. рис. 2) с тем, чтобы считывать двубайтные блоки с отступом в 4 байта от начала (то есть кратные шестнадцати значения).

В [1] приведено описание этой модификации. В частности, указано, что следует учитывать особенности планировшика. В [4] упоминается, что, к примеру, микроархитектура Intel Sandy Bridge имеет в своём распоряжении 2 исполнительных устройства для вычисления адреса (AGU - address generation unit), а также 3 ALU (arithmetic and logic unit), способные производить операции над векторными регистрами. Чтобы помочь планировщику выполнять загрузки блока из таблицы и суммирование по модулю 2 с результатом параллельно, можно использовать чередование регистров в этих командах (подробное описание использованных функций можно найти в [6]):

Листинг 5.3. LS-преобразование с использованием чередования регистров

ШІ28І vecl = mm load sil28 ( reinterpret castCconst m!28i*> ^^^^^^. ^^^^^^™                                                                                                 ^^^^^^™                        ^^^^^^™                           ^^^^^^™                                  '                                                                                                                                                                                   ^^^^^^™ ^^^^^^™

( t able+_mm_extract_epil6 (tmp2 , 0)+0x0000));

ml28i vec2 = mm load sil28 ( reinterpret casteconst m!28i*> ^^^^^^. ^^^^^^™                                                                                                 ^^^^^^™                        ^^^^^^™                           ^^^^^^™                                  '                                                                                                                                                                       ^^^^^^™ ^^^^^^™

( t able+_mm_extract_epil6 (tmpl , 0) + 0xl000));

vecl = _mm_xor_sil28 ( vecl , Cast Block ( t ab 1 e+_mm_extract _epil6 (tmp2 , l)+0x2000)); vec2 = _mm_xor_sil28 ( vec2 , CastBlock ( t able+_mm_extract_epil6 (tmpl , l)+0x3000));

vecl = _mm_xor_sil28 ( vecl , Cast Block ( t ab 1 e+_mm_extract _epil6 (tmp2 , 2)+0x4000 ) );

vec2 = _mm_xor_sil28 ( vec2 , Cast Block ( t ab 1 e+_mm_extract _epil6 (tmpl , 2)+0x5000 ) );

vecl = _mm_xor_sil28 ( vecl , Cast Block ( t ab 1 e+_mm_extract _epil6 (tmp2 , 7)+0xE000 ) );

vec2 = _mm_xor_sil28 ( vec2 , Cast Block ( t ab 1 e+_mm_extract _epil6 (tmpl , 7)+0xF000 ) );

data = _mm_xor_sil28 ( vecl , vec2 );

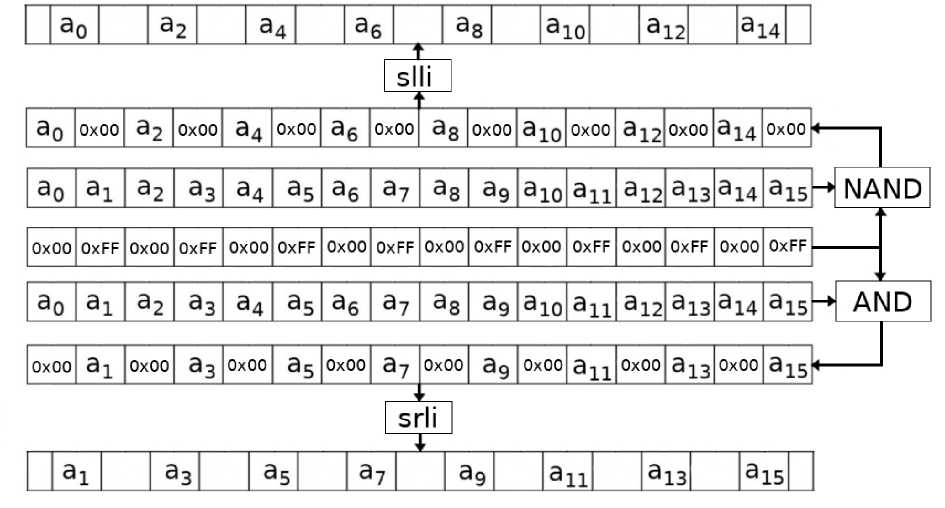
Рис. 2. Предвычислепие смещений

Предвычисление инструкций, которое было описано на рис. 2:

Листинг 5.4. Результат дизассемблирования предвычислепия смещений movdqa (% г s i ), %xmml movdqa %xmml,%xmm0

psrlq $0x4,%xmm0

psllq $0x4,%xmml movdqa 0x1876(%rip ) ,%xmm2

p a n d   %xmm2, % xmmO pextrw $0x0 ,%xmm0,%eax pand %xmm2,%xmml

0xl000(%rdx ,%rax , 1) ,%xmm2

Эти предварительные вычисления позволяют вычислять хог за две операции вместо трёх, что особенно важно, учитывая, что каждое применение LSX-преобразования представляет собой 16 итераций:

Листинг 5.5. Операция хог для случая с предвычислепием pextrw $0x0 ,%xmml,%еах xorps (%rdx ,%rax , 1) ,%xmm2

pextrw $0x1 ,%xmml,% eax xorps 0x2000(%rdx ,%rax , 1) ,%xmm2

pextrw $0x1 ,%xmm0,% eax xorps 0x3000(%rdx ,%rax , 1) ,%xmm2 •      •      •

В статье [1] авторы пришли к заключению, что скорость работы «Кузнечика» в реализации с использованием xmm регистров достигла своего предела. Хороший сравнительный анализ многочисленных вариантов реализации шифра с использованием LUT различных размеров дан в [3]. Из этого анализа следует, что наибольшая скорость работы достигается именно с использованием xmm регистров и LUT размером 64 кВ, описанной в этой статье. Примечательно, что реализация с использованием 256-битных регистров ymm и тем же LUT в 64 кВ по результатам этого анализа существенно проигрывает реализации на xmm регистрах.

3.    Использование AVX2 в режимах ЕСВ и СРВ

И всё-таки в отдельных случаях можно получить ускорение за счёт использования больших по размеру регистров. Мы предлагаем обрабатывать сразу два блока данных в некоторых режимах шифрования, используя расширенные до 256 бит векторные регистры (расширение набора инструкций AVX2, поддерживаемое с Intel Haswell и AMD Excavator). Это возможно в тех случаях, когда шифрование (или расшифрование) текущего блока возможно производить независимо от предыдущего. В этой работе были реализованы следующие режимы работы шифра:

• •    ЕСВ (Electronic Codebook)

е СВС (Cipher Block Chaining)

• •    CEB (Cipher Feedback)

• •    OFB (Output Feedback)

Данная оптимизация была осуществлена для шифрования и расшифрования в режиме ЕСВ и для расшифрования в режиме СЕВ. Попытка использовать ymm регистры непосредственно внутри LSX-преобразования не приводит к желаемому ускорению, так как загрузка 128-битных блоков в половинки регистра ymm занимает слишком много времени. Поэтому успешно использовать AVX2 для всех режимов не удаётся. Предлагается следующая модификация для режима ЕСВ: в половины 256-битного ymm регистра загружается по блоку открытого текста, применяется объединённое LSX-преобразование, аналогичное описанному в разделе 2.4. Различие заключается в том, что одним применением LSX- преобразования обрабатывается сразу два блока. Используются аналогичные предвычис-ления смещений с 256-битной маской (см. рис. 3), основанные на операциях И и НЕ И и битовых сдвигах на четыре бита.

Синим цветом показаны байты, относящиеся к смещению второго блока, srli и slli обозначают побитовый сдвиг на 4 бита вправо и влево соответственно. Два ymm регистра инициализируются в начале цикла и накапливают результат исполнения хог один для чётных, другой для нечётных байт. Ещё два ymm регистра необходимы, чтобы загружать в них данные на каждой итерации, выполнять хог с накапливающими регистрами и сохранять в эти регистры промежуточный результат:

Листинг 5.6. Использование AVX2 в режиме ЕСВ

data =  mm256 ________ ^^^^^^™ insertil28 _si256 (data, table + _mm256_extract_epil6 (tmp2 , 0) + 0x0000 , 0) data =  mm256 ________ ^^^^^^™ insertil28 _si256 (data, table + _mm256_extract_epil6 (tmp2 , 8) + 0x0000 , 1) vec2 =  mm256 ________ ^^^^^^™ insertil28 _si256 (vec2, table + _mm256_extract_epil6 (tmp2 , l) + 0x2000 , 0) vec2 =  mm256 ________ ^^^^^^™ insertil28 _si256 (vec2, table + _mm256_extract_epil6 (tmp2 , 9) + 0x2000 , 1) vecl =  mm256 ________ ^^^^^^™ insertil28 _si256 (vecl, table + _mm256_extract_epil6 (tmpl , 0) + 0xl000 , 0) vecl =  mm256 ________ ^^^^^^™ insertil28 _si256 (vecl, table + _mm256_extract_epil6 (tmpl , 8) + 0xl000 , 1) vec3 =  mm256 ________ ^^^^^^™ insertil28 _si256 (vec3, table + _mm256_extract_epil6 (tmpl , l) + 0x3000 , 0) vec3 =  mm256 ________ ^^^^^^™ insertil28 _si256 (vec3, table + _mm256_extract_epil6 (tmpl , 9) + 0x3000 , 1) data = _mm256_xor_si256 ( data , vec2 ) ;

vecl = _mm256_xor_si256( vecl , vec3 ) ;

В данном случае data и vecl выступают в качестве накапливающих регистров для хог чётных и нечётных байт соответсвенно. Такая схема позволяет учитывать особенности планировщика так же, как и в пункте 2.4. Однако Тб'Х-преобразование ускорится заведомо меньше, чем в два раза, из-за расходов на загрузку блоков в утш регистры и из-за ограниченного количества AGU (не более 3 штук). Аналогичным образом ускоряется расшифрование. Такую же идею можно применить для расшифрования в режиме СЕВ.

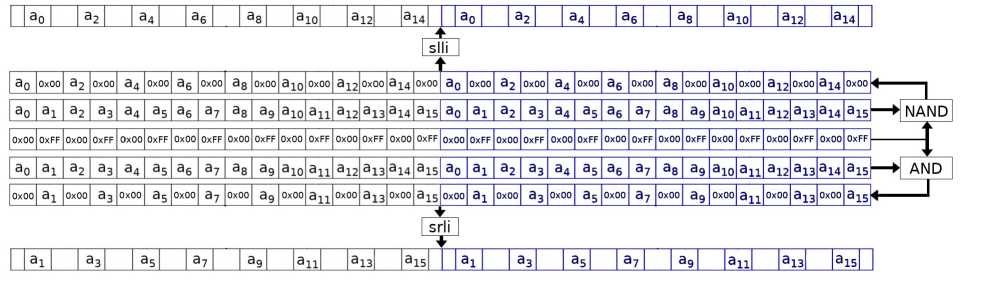
Рис. 3. Предвычисление смещений для модификации с AVX2

4.    Сравнительный анализ

В заключение приведём результаты для различных степеней оптимизации и различных процессоров (табл. 1, 2). Под baseline подразумевается реализация с Т-преобразованием через сдвиговый регистр; with LUT — реализация, в которой Т-преобразование выполнено при помощи LUT, но без использования xmm-регистров; LUT, хог — аналогично, но пред-вычисляется уже .^-преобразование, LSX объединено в одну функцию, для хог используется векторная инструкция; offset — использование xmm регистров и предвычисления смещений; AVX2 — описанная в пункте 3 модификация.

Таблица!

Скорость шифрования в режиме ЕСВ, Мб/с

	i3-4030u	i5-5200u	i5-7200u	i5-8250u
Baseline	6	8,8	10,2	П,4
With LUT	53	77	99	107
LUT, хог	69	99	131	139
Offset	79	113	135	142
AVX2	84	121	150	159

Т а б л и ц а 2

Скорость расшифрования в режиме CFB, Мб/с

	i3-4030u	i5-5200u	i5-7200u	i5-8250u
Baseline	5,2	8,7	10,2	9,4
With LUT	50	73	94	103
LUT, xor	73	105	131	145
Offset	80	118	135	150
AVX2	82	120	145	159

Более того, выбор компилятора тоже немаловажен. В работе [3] сравнивались результаты, полученные при комплияции с помощью Visual C++, Intel C++ и gcc. Нами было установлено, что наибольшая скорость достигается при компиляции clang (см. рис. 4).

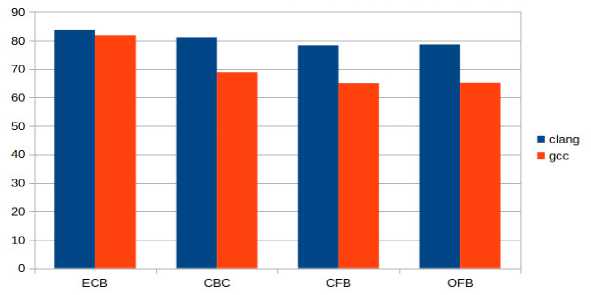
Рис. 4. Сравнение скорости работы (МБ/с) при компиляции clang и gcc (13-4030)

5.    Заключение

В данной статье подробно описаны известные на текущий момент методы оптимизации программной реализации блочного шифра «Кузнечик». Предложена модификация реализации для режимов ЕСВ и OFB, использующая расширение набора инструкций AVX2. Данная модификация даёт заметный прирост. Дальнейшее ускорение скорости работы шифра напрямую связано только с увеличением производительности процессоров и не может быть достигнуто программными методами (за исключением распараллеливания). Методы, описанные в этой статье и в [3], представляют собой программные модификации, ведущие к максимальному приросту скорости зашифрования и расшифрования. Исходный код реализации доступен по ссылке [7]