Реализация быстрого алгоритма преобразования Кирхгофа на примере бесселевых пучков

Решение задачи дифракции при непараксиальном распространении света в свободном пространстве остается актуальной проблемой. Основная сложность связана с большой вычислительной трудоемкостью реализации интегральных преобразований в оптике, вытекающей из быстроосциллирую-щего характера ядра этих преобразований. Известны алгоритмы, использующие быстрое преобразование Фурье (БПФ), однако при этом теряется информация о реальном масштабе получаемых распределений. К тому же, в некоторых случаях БПФ применить невозможно, например, при реализации интеграла Кирхгофа.

В данной работе рассмотрены свойства симметрии ядра интеграла Кирхгофа и разработан алгоритм вычисления, значительно сокращающий время расчета по сравнению с реализацией численного интегрирования «в лоб». Эффективность разработанного алгоритма исследована на примере бесселевых пучков.

представляет собой несколько более точную форму интеграла Кирхгофа.

Для программной реализации (2) «в лоб» можно воспользоваться численным интегрированием по методу трапеций:

I = [[ F ( 5 ’ П )d ^ ^d n =

1 NN                            ,      (4)

д ^S d У у ^^ ^{[ F} n - 1, m - 1 ^{+ F} n - 1, m ^{+ F} n , m - 1 ^{+ F} n , m ]

⁴     n = 2 m = 2

где S d - элементарная площадь области между отчетами плоскости интегрирования.

Чтобы использовать (4) для реализации алгоритмов вычисления оператора (2), исходное U ( 5 , п ) и выходное U ( x , y,z ) поле разбивают по отчетам [2], реальные координаты которых вычисляются по сетке:

5 = DIN ( n - N/ 2 ) ;

n m = D/N ( m - N 2 ) ,

x = D'/N ( i - N 2 ) ;   (5)

y j = D'/ N ( j - N / 2) , ⁽⁾

1. Описание алгоритма

Метод Кирхгофа решения дифракционных задач состоит в использовании интегральной теоремы, согласно которой значение функции U ( x , y,z ) на выходе, являющейся решением скалярного уравнения Гельмгольца:

где N x N - размер входной и выходной картины по отчетам; D x D - реальный размер входной и D' x D ‘ - выходной картин.

Воспользуемся формулой численного интегрирования (4) и разбиением входных и выходных массивов сеткой (5) для выражений (2) и (3):

д2 U (x, y, z) + д2 U (x, y, z) + дx2           ду2

■     '+к, и (x, y,z)=о дz

ikr

= U ( 5 , n m ) — | ik - -I , r У r )

можно выразить через значение функции U ( 5 , п , 0) на входе [1]:

где ^r = V⁽ x ^- 5 ^{) 2 + (} y j ^- n m ^{) 2 +} z ²;

л z D2

U (x,, y,, z) =---xx i j 2п 4 N2

ikr

U ( x , У , z ) = -у;- ff u ( 5 , П ) — | ik — | d 5 d n ,   (2)

2 п *V         r у     r )

N N x£Z[ Fn-1,m-1

n = 2 m = 2

+ F

+ F

^{+ 1} n , m - 1

^{+ F} n , m ] .

где r = 4(x - 5)2 +(У - n)2 + z2,

к = 2 п / А - волновое число, а X - длина волны светового пучка. Выражение (2) получатся через разложение светового поля по сферическим волнам и

Система (6) является простейшей реализацией непараксиального оператора распространения света на расстояние z от источника. Основным недостатком является большая ресурсозатратность алгоритма. Вызвано это тем, что подынтегральная функция - ikr из-за большого значения волнового числа к является быстроосциллирующей и приходиться выбирать очень мелкий шаг интегрирования.

В работе [3] была произведена оценка шага интегрирования, переписывая ее для рассматриваемого случая, получаем:

hR ^

7rd+z2 х

R D    N h

/= NM^{1 k - (} M ^{+ 1)/2} ) ; . у ^; = NM l ^{- (} M ^{+ 1)/2} ) .

Теперь не трудно переписать (6) используя (8),

где R D = D /2+ D '/2, N h - количество разбиений одного периода осцилляций T min (для алгоритма (6) предполагалось N h =10, см. рис. 1).

Выделим ядро интегрального преобразования (2):

(10), (11):

MM ikr

G n , m =    EE eV I ik - ¹ l где

^,     m ² k - !ы r ² I r J

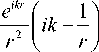
r = 7(x- + xk - ^n )2 + (У, + y'l- nm)2 +z2;

. F n , m = U( ^ n , n m ) G n , m ;                             (12)

и будем использовать для него шаг разбиения не крупнее, чем (7).

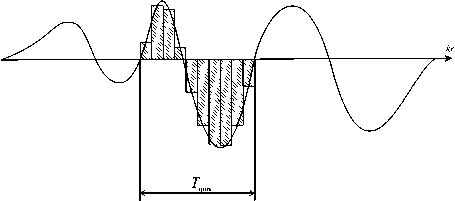
Рис. 1. Разбиение быстроосциллирующей функции Gr на области интегрирования, исходя из минимального периода биений Tmin

U ⁽ X, У_Р^z ) = ^-x ££ [ F n -„- , n = 2 m = 2

z D 2

---—г x

2 n 4 N ²

+ F . + F , + F  "I

n - 1, m      n , m - 1       n , m _

Необходимое число отсчетов не трудно вывести из (7):

M >

1 R d N h NJR^ ^х

При расчете выходного изображения легко заметить, что функция G_r периодически повторяется, поэтому можно сократить время выполнения алгоритма (12) при помощи табуляции G_n , _m . Действительно, из рис. 3 видно, что матрица табуляции значений G_r имеет размерность 2N-1 , что значительно сокращает время вычисления. Матрица G полностью покрывает все значения матрицы F , необходимые для подсчета любого U ( x i ,y i ,z ). На рис. 3 показано вычисление центрального значения U ( 0,0,z ), когда суммируются произведения соответствующих элементов заштрихованной области. Для вычисления произвольных значений U ( x i ,y_Dz ) соответственно матрица F перемещается по всей области матрицы G . Таким образом, вместо N 4 получаем 4N² операций.

Выражение (9) показывает, какое число разбиений функции G r является достаточным в области одного отчета входной функции для ее правильного «прописывания». На рис. 2 представлены дополнительные разбиения функции G r в области отсчета входной функции.

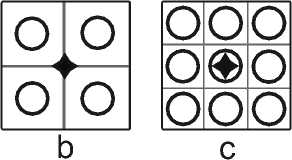
Рис. 2. Разбиение матрицы G на дополнительные отсчеты: (a) соответствует отсутствию разбиения (M=1), (b) двойному разбиению (M=2), (c) тройному (M=3)

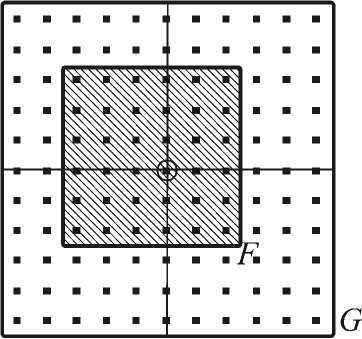
Рис. 3. Вычисление выходных значений при помощи перемножения соответствующих значений подынтегральной функции F на значения табулированной функции G

Используя разбиение на дополнительные отчеты (см. рис. 2) для (8) имеем:

^r = 7⁽ X ⁺ x' k- ^ n ^{) 2 + (} У, ⁺ У ’ ^- П _т ^{) 2 + z 2} ,      ^{(1 0)}

где

Далее можно еще больше ускорить вычисление функции (8), воспользовавшись свойством радиальной симметрии Gr. На рис. 4 в заштрихованной области показаны элементы Gn,m, которые не повторяются в матрице G, это составляет 1/8 всей матрицы. Далее ис- пользуется алгоритм радиальной развертки. В результате получаем оптимизацию вычисления в 8 раз.

различие с помощью среднеквадратического отклонения:

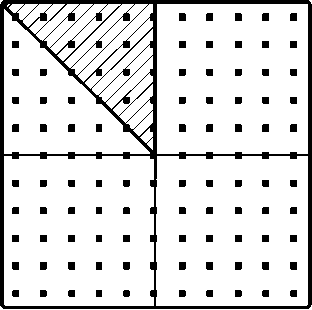
Рис. 4 Радиальная развертка матрицы G

∫∫ ( U ₀ ( x , y , z ) - U ( x , y , z ) ) ² d x d y Σ

∫∫ U ₀ ( x , y , z ) ² d x d y

Σ где U0(x,y,z) - комплексная амплитуда поля, вычисленная обычным алгоритмом численного интегрирования; U(x,y,z) - комплексная амплитуда поля, полученная оптимизированным методом. Для z=70 мм по формуле (14) получаем δ=10-11, при этом на одной и той же машине оптимизированный без развертки алгоритм рассчитывается в 845 раз быстрее обычного, а с разверткой в 1440 раз быстрее. Причем погрешность между результатами, полученными двумя последними алгоритмами равна машинному нулю.

Далее произведем расчет погрешности вычислений по формуле:

• 2.    Исследование алгоритма

Рассмотрим теперь результаты работы алгоритма полученного на основе выражения (12), но реализованного различными способами – через пересчет всех значений (обычный) и с табуляцией. В качестве входной функции U ( ξ , η ) возьмем одномодовый бес-селевый пучок:

U ( r , ϕ ) = C_{m , α} J_m ( α r ) exp( im ϕ ) ,              (13)

сформированный ДОЭ размером 5 × 5 мм , с параметрами моды m= 1, α = 7, C m, α = 1 (амплитудно-фазовая картина входного распределения показана на рис. 5).

• (а)                               (б)

Рис. 5. Амплитуда (а) и фаза (б) моды Бесселя с параметрами: m=1, α =7, C_{m, α}=1 во входной плоскости

Длину волны монохроматического лазерного пучка освещающего ДОЭ примем равной λ =633 нм . В первую очередь нас будут интересовать результаты в непараксиальной области - на расстояниях, не превышающих z= 70 мм от плоскости ДОЭ. Выберем количество отчетов входных/выходных изображений N= 100. Исходя из (9) примем нижний предел числа внутренних разбиений экспоненциальной функции M= 23. Для заданного z получим две выходные функции U₀ ( x,y,z ) и U ( x,y,z ), представленные на рис.6. Одна соответствует алгоритму с пересчетом всех значений (верхняя строка), другая алгоритму с табуляцией (нижняя строка). Визуально они ни чем не отличаются, однако мы можем оценить их

δ M

∫∫ ( U _{2 M} ( x , y , z ) - U _M ( x , y , z ) ) ² d x d y Σ

∫∫ U _{2 M} ( x , y , z ) ² d x d y

Σ

, (15)

где U_M ( x, y,z ) - комплексная амплитуда поля, полученная с числом дополнительного разбиения M , U_2M ( x,y,z ) - комплексная амплитуда поля с удвоенным числом разбиений. Для z =70 мм значение (15) получилось равным δ _M =0 ,05%.

На рис. 6 и в таблице 1 представлены результаты численных экспериментов по распространению бес-селевого пучка, показанного на рис. 5. Они демонстрируют практическое совпадение результатов, полученных обоими алгоритмами на всей непараксиальной области. При этом с уменьшением расстояния от входной плоскости оптимизированный алгоритм демонстрирует все большую эффективность в экономии машинного времени, что наглядно показано в таблице 1.

На рис. 7 показаны аналогичные результаты, но для параксиальных областей, полученные теми же алгоритмами (в связи с отсутствием визуальных различий приведены изображения только для одного алгоритма). В этом случае выигрыш по времени менее существенный, однако даже для дальней зоны ( z >2000 мм) обеспечивается ускорение в 4 раза при различии, равном машинному нулю (см. таблицу 1).

Из таблицы 1 видно, что погрешность отлична от нуля там, где число дополнительных разбиений M> 1, т.е. операция развертывания матрицы G вносит некоторое (несущественное) отличие в результаты. Таким образом, алгоритм с табуляцией позволяет вычислять интеграл Кирхгофа с той же точностью что и при использовании обычного алгоритма (если не использовать радиальную развертку) с ускорением не менее, чем в 4 раза. При использовании же дополнительных разбиений точность вычислений повышается.

с табуляцией            обычный

Рис. 6. Комплексное распределение моды Бесселя с параметрами: m=1, α =7, C_{m, α}=1 на различных расстояниях от экрана при использовании обычного алгоритма (верхняя строка) и с табуляцией (нижняя строка)

Таблица 1. Сравнение параксиальных и непараксиальных операторов

Расстояние от ДОЭ z, мм	Число отсчетов входной и выходной функции , N	Число разбиений экспоненциальной функции , M	Время выполнения обычного алгоритма ( час:мин:сек )	Время выполнения оптимизированного алгоритма ( час:мин:сек )	СКО между амплитудами обычного и оптимизированного алгоритма δ , %	Ускорение в K раз
1000	100	2	00:08:13	00:00:38	10-14	13
70	100	23	16:11:19	00:01:03	10-11	845
70	100	23	16:11:19	00:00:40*	10-11	1440
10	100	112	308:53:46	00:01:50	10-8	6836
1	100	152	-	00:02:59	-	-
1000	100	2	00:08:15	00:00:38	10-14	13
700	100	3	00:18:19	00:00:38	10-14	29
500	100	4	00:30:44	00:00:40	10-14	46
1000	130	2	00:23:18	00:01:48	10-14	13
2000	130	1	00:07:13	00:01:47	0	4
3000	130	1	00:07:26	00:01:51	0	4
4000	130	1	00:07:12	00:01:45	0	4
* - помечаются то время, которое получается при использовании радиальной развертки

z = 0 мм          z = 1000 мм        z = 2000 мм        z = 3000 мм        z = 4000 мм

Рис. 7. Комплексное распределение моды Бесселя с параметрами: m=2, α =7, C_{m, α}=1 на различных расстояниях от экрана

Заключение

В данной работе разработан быстрый алгоритм вычисления непараксиального интегрального оператора распространения лазерных полей в свободном пространстве. Алгоритм основан на использовании радиальной симметрии ядра интегрального преобразования и табулировании его значений. При этом повышение точности вычисления интеграла не за счет увеличения числа отчетов входной функции, а разбиении их на дополнительные отчеты для более детального представления быстро осциллирующего ядра преобразования, что существенно снижает вычислительную нагрузку.

При реализации всех предложенных способов оптимизации алгоритма удалось получить значительное ускорение его работы, благодаря чему для отдельно взятой задачи результат можно получить не за неделю работы программы, а за считанные минуты (см. табл. 1) притом, что по- грешность будет близка к погрешности машинных вычислений.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (CRDF Project SA-014-02), гранта РФФИ 05-01-96505, а также гранта INTAS 04-77-7198.