Реализация дискретного вейвлет-преобразования в системе остаточных классов специального вида

Обработка сигналов при помощи вейвлетов (от англ. wavelet – волна) в настоящее время является весьма перспективным направлением, которое является серьезной альтернативой традиционному преобразованию Фурье. Основная причина этого явления заключается в способности вейвлетов к быстрому получению как частотных, так и локальных особенностей обрабатываемого сигнала. Возможность быстро и качественно получать частотно-временную информацию об объекте привела к тому, что в настоящее время вейвлеты используются в обработке изображений, речи, видео, очистке от шума и сжатии информации [1-4]. Основным методом вейвлетной обработки сигнала является применение дискретного вейвлет-преобразования (ДВП) по схеме Малла [5]. Основой ДВП является применение фильтров с конечной импульсной характеристикой (КИХ-фильтров), которые могут быть весьма эффективно реализованы в системе остаточных классов (СОК).

СОК обладает большим потенциалом для увеличения производительности цифровых устройств благодаря замене операций сложения, вычитания и умножения чисел большой длины на параллельную обработку остатков гораздо меньшей разрядности [6]. Кроме того, СОК позволяет весьма эффективно проектировать и реализовывать различные цифровые устройства на программируемых логических интегральных схемах (FPGA) и интегральных схемах специального назначения (ASIC) [7]. Принципиальным недостатком СОК является сложность выполнения операции восстановления числа по его остаткам. В настоящей статье предлагается метод проектирования вейвлетных фильтров в СОК специального вида                    так как в таких

СОК можно в значительной степени уменьшить данный недостаток [8].

Система остаточных классов

В СОК числа представляются в базисе взаимнопростых чисел, называемых модулями для

Произведение всех модулей СОК          на зывается динамическим диапазоном системы. Любое целое число          может быть един ственным образом представлено в СОК в виде вектора                где                       [9].

Динамический диапазон СОК обычно делится на две примерно равные части таким образом, чтобы примерно половина диапазона представляла положительные числа, а остальная часть диапазона – отрицательные.

Таким образом, любое целое число, удовлетворяющее одному из двух соотношений: для нечетных и                    для четных , может быть представлено в СОК. Операции сложения, вычитания и умножения в СОК определяются формулами

Равенства (1)-(2) показывают параллельную природу СОК, свободную от поразрядных переносов. Восстановление числа по остаткам основано на Китайской теореме об остатках

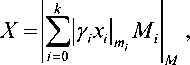
где              элемент           – мульти пликативный обратный для по модулю .

Другим методом преобразования числа из СОК в позиционную форму является переход к обобщенной позиционной системе счисления [10]. Число          имеет вид в обобщенной позиционной системе счисления, если:

A-l где

цифры числа в обобщенной

позиционной системе счисления, и x{ = x, тоски]; x2 = (x2 - Xj)c12 mod/7z2;

^xk = (-(k “XK -^ht ---^х'к-^_к-1,_к^тойтк.

Константы являются мультипликативными обратными элементами для   по модулю для всех            то есть                  для и могут быть вычислены, например, с помощью алгоритма Евклида.

Таким образом, можно выделить два основных преимущества модулярной арифметики.

• 1.    Арифметические операции сложения, вычитания и умножения выполняются без переносов, в отличие от позиционного представления чисел.

• 2.    Для каждого значения модуля арифметические операции выполняются с парой соответствующих вычетов параллельно, при этом вычеты имеют гораздо меньшую разрядность, чем исходные операнды X и Y .

Основной проблемой СОК является сложность выполнения операции деления и сравнения двух чисел. Однако несмотря на указанные недостатки, модулярная арифметика может быть эффективно реализована в приложениях, где основная доля вычислений приходится на операции умножения в сочетании со сложением и вычитанием [11]. Как будет видно далее, фильтрация сигналов является именно таким приложением.

Дискретное вейвлет-преобразование в системе остаточных классов

ДВП определяется последовательностью вложенных, закрытых подпространств, где           – про странство последовательностей, суммируемых с квадратом. Подпространства удовлетворяют следующему свойству полноты,

.

Допустим, что любой элемент из     мо жет быть единственным образом представлен в виде суммы двух элементов из            где

Для ортогональных вейвлетов определяется как ортогональное дополнение           Существует последовательность такая, что            является бази сом в Это означает, что последовательность может быть построена так, что будет базисом в . Применив такой метод разложения J раз, можем получить следующее разложение для :

Одномерное ДВП -го порядка последовательности определяется рекуррентными равенствами

Х-1

^'? = ^Skat-k ,i = \2-J-,

^=0

t/^ = "y.Mln-k ’ а^ = Хп ’ к=0

где          – аппроксимирующие и детализирующие последовательности i-го уровня;     и hk (^ = 0;1...7V-l) описывают коэффициенты соответственно низкочастотного и высокочастотного фильтров. Исходный сигнал   может быть точно восстановлен из коэффициентов кратномасштабного разложения по формуле

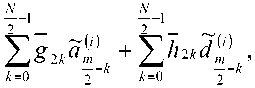
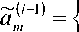
т -четное число;

Т§2к^^1 , ⁺ H^h^^d^ ' к=0          ₂^к к=0          2 ^к

т- нечетное число, где gk и hk являются коэффициентами низкочастотного и высокочастотного синтезирующих фильтров соответственно.

Как можно видеть, в (8) используются операции сложения и умножения. Использование только этих операций для вычисления ДВП позволяет наиболее полно использовать возможности модулярной арифметики для повышения быстродействия систем цифровой обработки сигналов по сравнению с системами, функционирующими в традиционных позиционных системах счисления.

Построение вейвлетных наборов фильтров при помощи СОК обладает рядом преимуществ. Если коэффициенты вейвлетного фильтра зафиксированы априори, то использование умножителей на основе LUT-таблиц будет весьма эффек- тивным решением, обеспечивающим высокую скорость вычислений и эффективность с аппаратной точки зрения [12].

Приведем формулы, по которым осуществляется прямое и обратное дискретное вейвлет-преобразование в СОК. Каждая из формул задает преобразование для отдельно взятого модуля, число модулей берется таким, чтобы покрыть требуемый диапазон вычислений; формулы для каждого из модулей аналогичны приведенным:

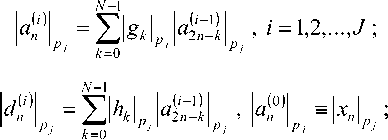
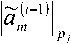
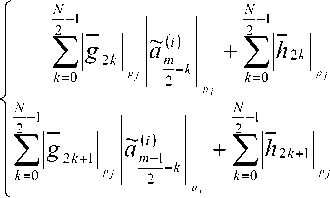
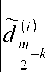
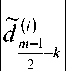
, m-четное число;

m-нечетное число.

Проектирование вейвлетного фильтра в системе остаточных классов

Для моделирования вейвлетного фильтра в СОК был выбран вейвлет Добеши Db4, так как семейство вейвлетов Добеши обладает весьма важным во многих приложениях свойством ортогональности образуемого базиса [13-14]. ДВП можно реализовать при помощи комбинации КИХ-фильтров так, как это показано на рис. 1.

Коэффициенты высокочастотного анализирующего КИХ-фильтра Н , соответствующего рассмотренному вейвлету Db4, приведены в таблице 1. Коэффициенты остальных фильтров ^D ’ Н_R и Lr для данного вейвлета могут быть легко получены из коэффициентов н _D путем перестановки коэффициентов и смен знака, так как схема, изображенная на рис. 1, является набором фильтров со свойством точного восстановления сигнала [15].

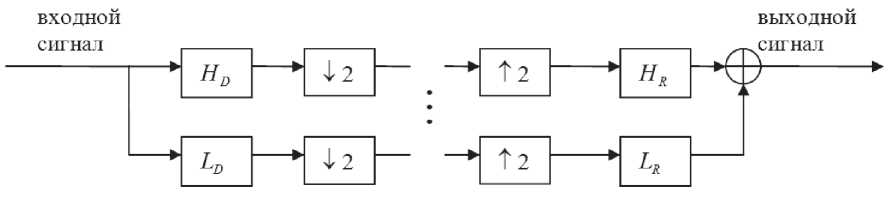
Рис. 1. Дискретное вейвлет-преобразование сигнала.

Целочисленное значение коэффициентов фильтра Db4 в таблице 1 было получено преобразованием чисел двойной точности в числа шириной 10 бит, из которых 1 бит отведен для знака, а остальные 9 являются информационными. Описанный переход осуществлялся путем умножения исходных коэффициентов на 2⁹ = 5 12 с последующим округлением результата. Полученное целочисленное значение было переведено в СОК вида {2^й-1, 2",2"+1}, при и = 7, то есть {127,128,129}. Выбор такой СОК обусловлен тем, что для таких наборов модулей разработаны эффективные алгоритмы выполнения проблемной операции обратного преобразования числа из СОК в ПСС [8].

Выбранная СОК задает диапазон равный log2 (127-128-129)» 20,999912 бит, в то время как максимальный отклик фильтра равен У|6, =675, что соответствует «9,398744 битам. Таким образом, данный фильтр можно использовать для обработки [20,999912-9,398744] = 11-битных последовательностей входных данных, не опасаясь переполнения динамического диапазона системы.

Magnitude Response (dB)

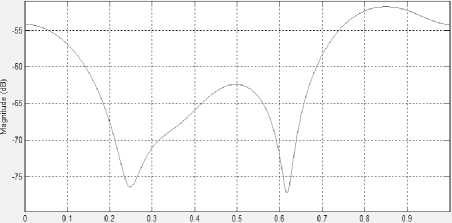
Normalized Frequency (xi rad/sample)

Рис. 2. АЧХ ошибки округления фильтра Db4

Основной характеристикой любого КИХ-филь-тра, в частности вейвлетного фильтра Db4, является его импульсная характеристика. Импульсной характеристикой цифровой системы называется отклик, выдаваемый при подаче на вход системы единичного сигнала <5(77) . В рассматриваемом нами случае при преобразовании числа в целочисленную форму единичный сигнал должен быть умножен на 29 =512, так как указанное преобразование выполнялось путем сдвига двоичного числа на 9 разрядов влево:

/ a [512, £>(») = ]

[0, n = 0, 77 * 0.

Таблица 1. Коэффициенты фильтра Db4 в ПСС и СОК

Db4, позиционная форма	Целочис ленное значение	Db4 в СОК {127,128,129}
0,162901714025649	83	{83, 83, 83}
0,505472857545915	259	{5,3,1}
0,446100069123380	228	{101, 100, 99}
-0,019787513117822	-10	{117,118,119}
-0,132253583684520	-68	{59, 60,61}
0,021808150237089	11	{11,11,11}
0,023251800535491	12	{12, 12, 12}
-0,007493494665181	-4	{123,124,125}

Разумеется, перевод коэффициентов фильтра в целочисленную форму 10-битного представления приводит к ошибкам округления. На рис. 2 показана амплитудно-частотная характеристика (АЧХ) этой ошибки для фильтра Db4. Видно, что максимальное значение ошибки не превосходит –50 Дб, что на практике является достаточно хорошим результатом, не приводящим к сколько-нибудь значимым искажениям обрабатываемого сигнала [16].

При переходе к СОК {127, 128, 129} имеем

J{4,0,125},       /2 = 0,

{0,0,0}, 77^0.

На рис. 3 изображены импульсные характеристики каждого из модулярных фильтров.

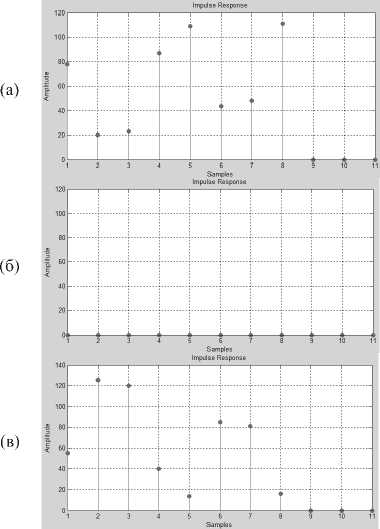
Рис. 3. Импульсные характеристики фильтра Db4 в модулярной форме: а) m_x =127, б) 772, =128, в) m₃ =129

На рис. 4 представлена ошибка импульсной характеристики, полученная в результате перевода коэффициентов фильтра в СОК, с округлением. Максимальное значение ошибки по модулю не превосходит амплитуды подаваемого на вход фильтра импульса, что составляет менее 0,1% обрабатываемого сигнала. Таким образом, предложенная архитектура вейвлетного фильтра в СОК может быть использована в большинстве практических случаев за исключением тех, при которых требуется особая точность обработки.

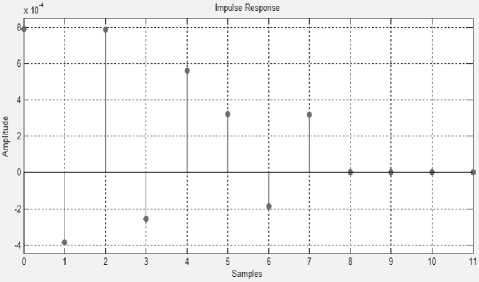
Рис. 4. Ошибка импульсной характеристики фильтра Db4 в модулярной форме

Заключение

В статье предложен метод проектирования вейвлетных фильтров в СОК. Показано, что СОК обладает большим потенциалом для увеличения производительности фильтров, так как в рассматриваемой задаче требуется выполнение только операций сложения и умножения, которые можно очень быстро вычислять в модулярной форме.

На примере фильтра Добеши Db4 показано, как можно преобразовать коэффициенты из позиционной системы счисления в СОК. Результаты моделирования показали, что ошибка округления, неизбежно возникающая при таком переходе, не вызывает значимых отклонений в работе фильтра.

Построенный метод может быть успешно применен для реализации устройств цифровой обработки сигналов на программируемых логических интегральных схемах, а также в проблемно-ориентированных аппаратно-программных решениях для обработки видеоизображений,