Реализация гибридных алгоритмов контроля и диагностики газотурбинного двигателя с использованием современных бортовых вычислительных устройств

применяется метод допускового контроля, который заключается в том, что отслеживается нахождение измеряемых величин и их производных по времени в заданных пределах, при выходе за которые делается заключение об отказе. При обнаружении отказа измерительного канала для восстановления потерянной информации используется последнее достоверное значение измеряемого параметра. Эффективность такого метода в случае постепенного или плавающего отказа низка, а также невысока точность восстановленной информации, в особенности при работе двигателя на переходных режимах. Для решения данной проблемы возникает необходимость дополнять классические методы контроля и диагностики ГТД интеллектуальными методами, имеющими более высокую эффективность на любых режимах [3]. Из вышеуказанных методов, помимо нейронных сетей и алгоритмов нечеткой логики, представляют интерес гибридные интеллектуальные алгоритмы, реализованные на основе комбинации различных интеллектуальных методов. Так, для решения указанной задачи может быть использована интеллектуальная система, в основе которой лежит нейросетевая математическая модель и нейро-нечеткий классификатор [2]. Такая система позволяет обнаруживать и классифицировать нештатные режимы работы ГТД, измерительных каналов и исполнительных механизмов в бортовых условиях (рис. 1).

Математическая модель ГТД. Математическая модель ГТД играет роль эталонной модели в составе бортовой системы контроля и диагностики. Сравнение расчетных данных математической модели с данными измерительных каналов позволяет отследить изменения в контролируемом объекте.

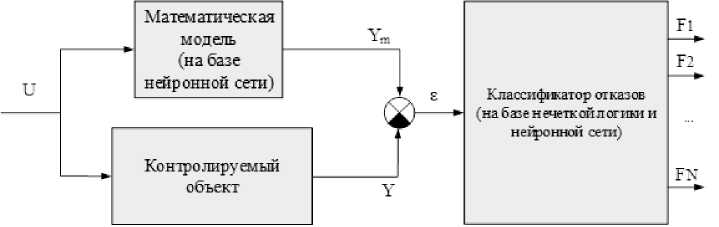
Рис. 1. Структура системы контроля и диагностики

Кроме того, данная модель может быть применена для восстановления данных в отказавшем измерительном канале. Математическая модель должна обладать рядом качеств, важнейшими из которых являются следующие [6]: - модель описывает нестационарность рабочих процессов ГТД (таким образом, необходимо использование динамической модели);

• -    структура математической модели ГТД обеспечивает практическую возможность ее функционирования в комплексе с математическими моделями других элементов летательного аппарата.

  

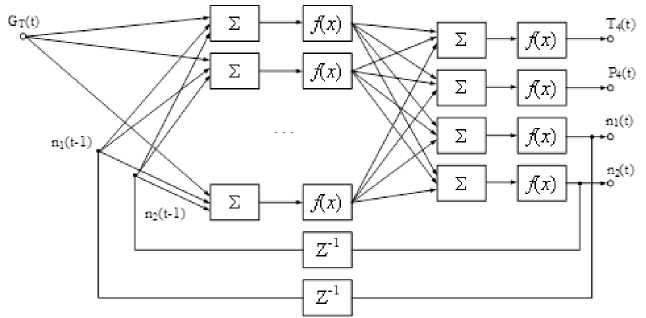
  Рис. 2. Структура нейросетевой модели ГТД

  
  

Одним из перспективных направлений в данной области является создание математической модели на основе нейронных сетей, которые отличаются способностью к обучению и обобщению накопленных знаний, что дает возможность подстраивать параметры модели под свойства конкретного экземпляра двигателя на основе данных, полученных в результате стендовых и полетных испытаний. Вышеуказанным требованиям к математической модели отвечают рекуррентные нейронные сети, такие как сети Элмана и многослойные персептроны с общей обратной связью (NARX) [5].

Создание и настройка математической модели ГТД осуществляется с использованием Neural Network Toolbox – пакета расширения среды MATLAB. На рис. 2 показана структура нейросетевой модели ГТД, построенной на основе многослойного рекуррентного персептрона (NARX). Количество нейронов в скрытом слое выбирается исходя из минимальной среднеквадратической ошибки обучения нейронной сети

(рис. 3). Выборка экспериментальных данных для обучения модели приведена в табл. 1.

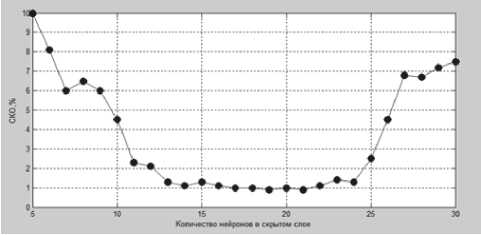
Рис. 3. Ошибка нейронной сети в зависимости от количества нейронов скрытого слоя

Классификатор отказов ГТД и его систем. Классификатор состояния двигателя и его систем построен на основе нейро-нечеткой сети. Принцип его работы заключается в следующем: вектор расчетных данных модели Ym (рис. 4) сравнивается поэлементно с вектором измеренных данных Y, затем полученный вектор ошибок ɛ подается на вход нейро-нечеткого классификатора, который на основании значения ошибок и их производных по времени выдает заключение об исправности двигателя или его систем.

Таблица 1. Обучающая выборка математической модели

G t	n 1	n 2	T 4	P k
116.125	9.664	20.867	833.375	1.125
125.750	10.000	21.758	817.125	1.093
131.125	10.477	22.249	843.437	1.121
132.875	10.820	22.813	860.250	1.144
136.000	11.266	23.414	879.438	1.174
138.375	11.711	24.047	902.250	1.181
139.125	12.305	24.930	933.813	1.202
143.875	12.836	25.758	955.250	1.215
145.750	13.461	26.742	974.687	1.229
208.000	36.742	61.336	616.688	3.196
243.375	43.273	65.945	640.125	3.902
319.500	54.047	71.695	635.688	5.267
425.000	67.203	77.258	637.063	7.135
481.250	72.883	79.461	639.500	8.122
524.250	75.492	80.695	647.625	8.732
582.875	78.594	82.008	663.313	9.404
624.875	80.797	82.906	677.063	9.958

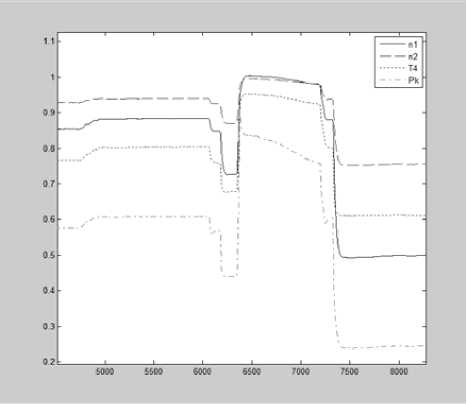
Рис. 4. Расчетные данные нейросетевой модели ГТД

Выходными     сигналами     такого классификатора являются следующие состояния двигателя и систем: - исправное состояние - отказы измерительных каналов - отказы исполнительных механизмов - отказы ГТД - отказы системы автоматического управления

Моделирование нейро-нечеткого классификатора производится с использованием набора инструментов ANFIS editor математического пакета MATLAB на основе данных полученных в ходе полетных испытаний ГТД, а также результатов моделирования отказов ГТД и его систем с использованием полной поэлементной математической модели ГТД [7].

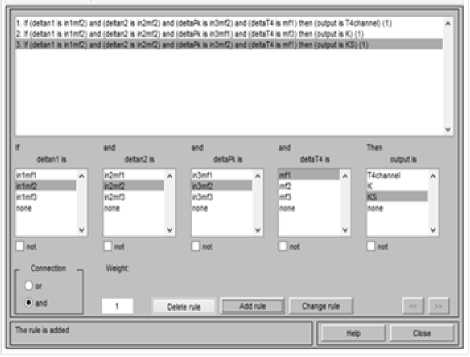
Рис. 5. Правила нечеткого вывода классификатора отказов

Процесс проектирования классификатора отказов состоит из следующих основных этапов [4]:

• -    формулировка набора правил нечеткого вывода на основании сведений о соответствии ОТКлонения измеренных данных от расчетных той или иной неисправности;

• -    построение нейронной сети, являющейся основой системы нечеткого вывода;

• -    обучение нейронной сети с использованием эталонной выборки входных и выходных данных, представляющих собой массивы экспериментальных данных измерительных каналов ГТД;

• -    подстройка параметров входных функций принадлежности.

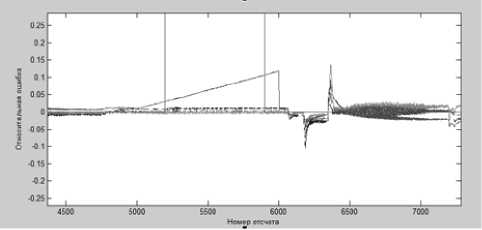
Рис. 6. График выборки обучения классификатора отказов

На рис. 5 показан пример задания правил нечеткого вывода данного классификатора в процессе его отладки в ANFIS-редакторе. Для обучения классификатора были скомпонованы обучающие выборки – входные измеренные и расчетные данные каналов n1, n2, Pk, T4, включающие отклонения, полученные путем моделирования отказов двигателя и датчиков, а также выходные эталонные данные, представляющие собой сигнал о соответствующем отказе. На рис. 6 изображен график выборки обучающих данных, в которых моделируется постепенный отказ датчика температуры газов. Сравнительный анализ точности классического и нейро-нечеткого методов классификации отказов приведен в табл. 2. В ней отображены вероятности ошибок 1 и 2 рода при классификации отказа измерительного канала температуры газов за турбиной, дефектов компрессора и камеры сгорания. Данные, приведенные в табл. 2, доказывают, что интеллектуальные методы более эффективно и качественно осуществляют процесс идентификации отказов в узлах и агрегатах ГТД.

Таблица 2. Сравнительный анализ методо в

Метод классификации отказов	Вероятность ошибки определения отказа, %
	отказ измерительного канала t4		дефект компрессора низкого давления		дефект камеры сгорания
	ошибка 1 рода	ошибка 2 рода	ошибка 1 рода	ошибка 2 рода	ошибка 1 рода	ошибка 2 рода
допусковый контроль	1,21	0,75	1,72	1,17	2,41	1,93
интеллектуальный метод	0,47	0,27	0,56	0,41	0,77	0,55

Аппаратная реализация гибридных алгоритмов в бортовых условиях. Выполнение нейросетевого алгоритма заключается в вычислении выходных сигналов нейронов на основе входных сигналов и весовых коэффициентов от начального до конечного слоя. Математическая модель нейрона следующая:

n y=f IE wx + b I

V i =1              J •

;

где wi – вес синапса, i = 1…n, n – число входов нейрона, b –значение смещения, xi – входной сигнал, y – выходной сигнал, f – функция активации. Для повышения быстродействия нейросетевого алгоритма целесообразно использование в качестве функции активации нейронов скрыто- го слоя

функции f ^{( 5} )   a _|_|_s|

(рациональная сиг-

моида), требующей малого объема вычислений по сравнению с экспоненциальной функцией или функцией гиперболического тангенса. Нейроны выходного слоя имеют линейную функ- цию активации.

В настоящее время рассматривается реализация нейросетевого алгоритма на базе 16-разрядного микроконтроллера ST10F269 фирмы STMicroelectronics[8]. Микроконтроллеры этой серии получили широкое распространение в современных цифровых системах автоматического управления, в том числе и в бортовых вычислительных устройствах. Наличие в составе ядра данного контроллера модуля умножителя-накопителя (MAC) позволяет увеличить скорость вычисления алгоритма за счет совмещения операций умножения и сложения при взвешенном суммировании в сумматоре нейрона.

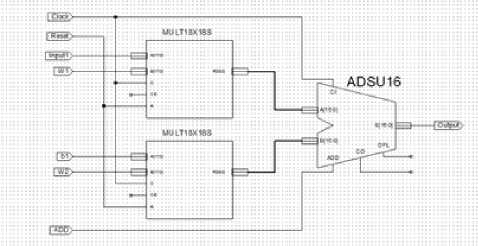
Рис. 7. Структурная схема искусственного нейрона

При необходимости повышения точности алгоритмов и усложнения их структуры, что приведет к увеличению числа искусственных нейронов, и, соответственно, увеличению количества выполняемых вычислительных операций, может быть целесообразной реализация данных алгоритмов на базе более скоростных вычислительных устройств по сравнению со штатным микроконтроллером. Такие устройства могут быть реализованы на основе цифровых сигнальных процессоров, программируемых логических интегральных схем (ПЛИС) либо специализированных процессоров. Так как нейросеть является параллельной вычислительной структурой, существенным фактором при выборе элементной базы для вышеуказанного устройства является возможность реализации параллельных вычислений. В данном случае применение ПЛИС наиболее оправдано по следующим причинам: архитектура вычислительного устройства на ПЛИС может быть оптимизирована под любую структуру алгоритма, количество параллельных процессов ограничивается только количеством логических ячеек в микросхеме, имеется выбор термостойких и радиационно-стойких микросхем ПЛИС, пригодных для применения в бортовых условиях. Распараллеливание вычислений позволяет реализовать нейросетевой алгоритм за единицы тактов, что при тактовой частоте ~ 100 МГц составит десятки наносекунд. Для реализации нейросетевых алгоритмов с высоким быстродействием была выбрана серия ПЛИС Xilinx Virtex [9]. Для разработки и отладки конфигурации используется среда разработки Xilinx ISE. Для ускорения разработки искусственный нейрон реализован в виде блока конфигурации (рис.7), на основе которого может быть создана нейронная сеть любой сложности.

Выводы:

В ходе работы были установлены следующие преимущества использования нейросетевых и нейро-нечетких алгоритмов для решения вышеуказанных задач: повышение эффективности диагностики плавающих отказов; простота обучения и дообучения применяемых моделей; точность вычислений в условиях «не-факторов». Был описан процесс реализации данных алго-ритов на бортовых вычислительных устройствах, и показаны преимущества ПЛИС как элементной базы для таких устройств.