Реализация искусственных нейронных сетей в непозиционной системе счисления для автоматизированных систем управления

Одним из методов реализации механизма автоматизированных систем управления в современных условиях является использование нейронных сетей.

Для представления и обработки данных в искусственных нейронных сетях (ИНС) могут быть использованы позиционные и непозиционные системы счисления. Позиционные системы традиционны, и для согласования их с ИНС используются искусственные приемы, которые снижают положительные свойства искусственных нейронных сетей, связанные с параллельными вычислениями. Непозиционные системы счисления, в частности система остаточных классов (СОК), – это параллельные системы, они обеспечивают параллелизм на уровне выполнения элементарных операций, т.е. система остаточных классов выступает естественной основой представления данных в ИНС, служащих их новыми свойствами и возможностями. Этот симбиоз жизненно необходим для исследования ИНС, являющихся базой разработки нейрокомпьютеров, функционирующих в системе остаточных классов. Система в остаточных классах – естественная система счисления для кодирования информации в ИНС, так как математические модели системы остаточных классов и искусственных нейронных сетей являются адекватными моделями [5].

ИНС в СОК – это параллельные взаимосвязанные сети простых элементов, которые предназначены для взаимодействия с объектами реального мира таким же образом, как взаимодействуют биологические нервные системы. Такие сети могут выполнять не только задачи, обладающие естественным параллелизмом, но и некоторые сложные и творческие задачи, реализация которых традиционными методами неэффективна. Для повышения эффективности решения задач возникает необходимость использования ИНС, обладающих свойствами, сходными со свойствами человеческого мозга. При сравнении человеческого мозга с современными компьютерами фон Неймана в плане обработки информации можно заметить, что время переключения искусственных нейронов (несколько миллисекунд) примерно в миллион раз медленнее, чем время переключения элементов современного компьютера, но они имеют в тысячи раз большую соединяемость, чем современный компьютер.

Если входы ИНС сетей с их синаптическими весами отожествить с разрядами чисел, представленных в системе остаточных классов, то ИНС станет натуральным представлением СОК. Соединение естественного параллелизма ИНС и системы остаточных классов создает предпосылки для разработки вычислительных средств с массовым параллелизмом. Кроме того, сочетание свойств ИНС и системы остаточных классов не только реализует массовый параллелизм, но и позволяет с новых позиций разрабатывать отказоустойчивые вычислительные средства. Параллельные вычислительные структуры являются идеальной основой для построения устойчивых к отказам нейрокомпьютерных средств сверхвысокой производительности.

Большинство нейронных алгоритмов включает в себя прежде всего повторяющиеся и регулярные операции. Их можно эффективно отобразить в параллельных структурах.

В ИНС все нейроны работают конкурентно, а на вычисление непосредственно влияет знание, зашифрованное в соединениях сети [1, 4, 5]. Искусственные нейроны объединяются – 44 – в слои. Слой представляет собой совокупность ИН с единым входным сигналом, не имеющих связей между собой. Соотношение, связывающее вход и выход ИН в слое, записывается в следующем виде:

N y = f (У a х x + b ),     m = 1, M,                              (1)

ym     m mn mn m ,               , , n=1

где М - число ИН в слое; x = ( x 1, x ₂,..., x_N ) - входной сигнал слоя ИН; b = ( b 1 ,b ₂,..., b_N ) - вектор смещения, матрица весовых коэффициентов слоя ИН; f_m ( ° ) - функция активации т -го ИН

_ m = 1, M

A = (amn )        в слое; Ут - выходной сигнал т-го ИН в слое. Слои ИН могут объединяться в n = 1, N нейронную сеть. Соотношение вход-выход m-го ИН j-го слоя сети таково:

Nj yj, = fj (Z j x xj + bjj), m, = 1, M,, j = 1, J,                      (2)

n = 1

остальные символы имеют те же значения, что и в соотношении (1), и относятся к j -му слою. Между слоями могут быть установлены связи различного вида. В общем случае выход слоя с номером j подается на вход слоя j+s (рис. 1). Связи называют: последовательными, если s = 1; перекрестными, если 5 > 1 обратными, если 5 < 1.

,,

Если искусственный нейрон (ИН) каждого слоя имеет единую функцию активации f j_i = f ^j ( o ) V j , такую ИНС называют однородной [1, 5]. ^j

Вычисления в искусственных нейронных сетях существенно отличаются от традиционных. В силу высокой распараллеленности их можно рассматривать как коллективное явление. В нейронных сетях нет локальных областей, в которых запоминается конкретная информация. Запоминание информации происходит распределенным образом по всей сети путем модификации весов и порогов. Следствием этого служит то, что ИНС практически индифферентна к потере части вычислительных элементов (нейронов) в процессе работы [5].

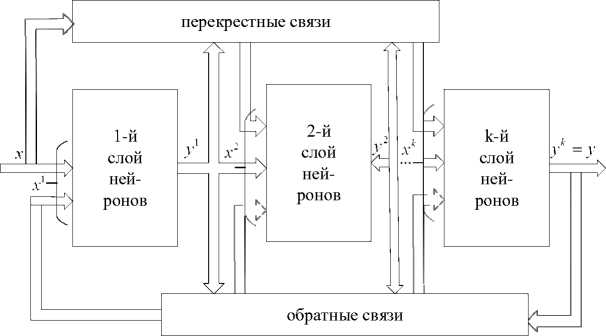
Рис. 1. Многослойная нейронная сеть с перекрестными связями

Fig. 1. Multilayer neural network with cross links

В СОК число X кодируется набором остатков ( а. , а₂ ,..., а „) от деления X на заданные ¹²

(ai = |Х|р ,(i = 1,n)), модули pi,p2,...,Pn — основания системы |X|p, символом обозначается элемент множества р ={0,1,..., p -1} сравнимый с величиной X по модулю р,. Если основания СОК попарно просты ((P-,Pj) = 1, i, j = 1,n, i * J) то согласно китайской теореме об остатках модулярному коду (ava2,...,an) (ai е р р , i = 1,n) соответствует класс вычетов по модулю P, задаваемый сравнением               i nn

X = Z a.B.(modP ) = Z a B- Г х Р ,                              (3)

n                               i = 1

где P = П p i , B i - ортогональные базисы СОК; r_X - ранг числа X, показывающий, сколько раз i = 1

диапазон системы P был превзойден при переходе от представления числа в СОК к его позиционному представлению через систему ортогональных базисов, которые являются константами для заданной системы оснований. Так как сравнения по одному и тому же модулю можно почленно складывать, вычитать и перемножать, то арифметические операции в кольце вычетов по модулю P сводятся к соответствующим операциям над одноименными цифрами модулярного кода операндов по модулям р i , р 2 ,^, р_т т.е. выполняется по правилу

|A o B P = (| « 1 o Р 1\p , ^ 2 о Р 2\р_г ,..., k o в.. . ),                                      (4)

где А и В имеют соответственно модульные коды ( а 1 , а ₂,..., а_п ) и ( Д , Р 2 ,..., p n ), o е { + , - , х } .

По принципу построения СОК каждый остаток ai е o , (i = 1, k) несет информацию обо Pi всем исходном объекте G, описываемом информационном кодом л,(/ = 1,P) а диапазон представляемых кодовых комбинаций (чисел X ) определяется как (0, Р-1).

l

Нейронные вычисления - это проблема для любого уровня последовательных и параллельных ЭВМ. Для каждого вида вычислительной системы нейронные вычисления - проблема супервычислений, проблема достижения большей производительности при тех же ресурсах.

Для эффективных нейровычислений необходимо как можно быстрее выполнять операции перемножения с суммированием результатов, что и обуславливает целесообразность применения СОК в нейросетевых алгоритмах.

С одной стороны, появляется необходимость использования модульных кодовых конструкций в нейрокомпьютерных вычислительных средствах для повышения их отказоустойчивости и ускорения нейрообработки. С другой стороны, в полной мере эффективная реализация СОК может быть достигнута за счет использования адаптивных свойств самих нейронных сетей [2, 3, 5].

Предпосылкой к созданию нейрокомпьютерных вычислительных средств на основе аппарата системы остаточных классов является семантическое сходство математических моделей нейронных сетей и системы остаточных классов:

• 1.    Математической модели СОК и формального нейрона

• 2.    Математической модели СОК и перцептронов (простейших многослойных ИНС)

nnN

X = Е ^a i^Bi (mod ^P ) = Е ^a i^Bi ^- r x P ^ y = f ( T, x n ^x a n ⁺ b ).            (⁵)

i = 1                                i = 1                                          n = 1

nn     Nj jjjjj

X Z^ ^ i B i (mod P ) / , ^ai B i r X P ^ y mj f mj ( ^ x j ^X a mn j + b m j ) i = 1                               i = 1                                                n j = 1

Таким образом, реализация искусственных нейронных сетей в непозиционной системе счисления для автоматизированных систем управления заключается в реализации арифметики СОК в нейросетевом логическом базисе. Структура алгоритма обработки данных, представленных в системе остаточных классов, как и структура ИНС, обладает естественным параллелизмом, что позволяет использовать ИНС в качестве формального аппарата описания алгоритмов. Кроме того, алгоритмы с ярко выраженным естественным параллелизмом, например обработка сигналов, не используют режима обучения, вместе с тем органически вписываются в нейросетевой логический базис [1]. С этой точки зрения алгоритмы модулярных вычислений соответствуют алгоритмам вычислений с помощью базовых процессорных элементов (искусственных нейронов). По этой причине схемы в СОК адекватны схемам на основе нейросетевого базиса. Искусственные нейронные сети и основные модулярные структуры представляют собой коннекционные устройства, полученные последовательным соединением между собой базовых элементов. Нейронные и модулярные образования будут послойно определены, если задан алгоритм соединения базовых элементов. Аппаратная реализация ИНС, функционирующих в СОК, характерна и для нейроподобных образований, которые обладают максимальным естественным распараллеливанием и служат базой для разработки нового класса вычислительных структур.