Реализация метод а экономного кодирования Хаффмана в информационно-телеметрических системах

Вводные замечания

Необходимость в контроле все более сложных технических средств, объединение их в системы, функционирование которых обеспечивается за счет обмена внутрисистемной информацией, все больше актуализирует вопросы телеметрического обеспечения. В той или иной постановке требуют решения вопросы увеличения количества и частоты опроса телеметрируемых параметров, миниатюризации телеметрических средств, минимизации удельного расхода энергии на единицу информации, увеличения скорости передачи информации [7].

Качественный рост современной электронной базы в той или иной мере способствует решению данных вопросов, однако часто решение задачи «в лоб» только за счет повышения скорости выполнения операций и увеличения доступных объемов памяти не является оптимальным, а иногда и вовсе не позволяет достичь желаемых результатов. В связи

Реализация метода экономного кодирования Хаффмана ...

с---------------------------------------------------------------------------------------------------------------\

Артюшкин Андрей Борисович кандидат технических наук, доцент, доцент кафедры телеметрических систем, комплексной обработки и защиты информации Военно-космической академии им. А.Ф. Можайского. Сфера научных интересов: системы цифровой связи, кодирование данных. Автор более 30 опубликованных научных работ.

с этим наряду с использованием все более совершенных электронных компонентов в составе устройств обработки информации активно ведется совершенствование алгоритмов преобразования и обработки данных.

В частности, для повышения скорости передачи данных при доступной операционной частоте могут использоваться методы экономного кодирования. Данные методы позволяют сокращать передаваемый объем данных исходя из соображения, что более часто встречающиеся в сообщении информационные единицы должны передаваться кодовыми последовательностями меньшей длины, нежели единицы с меньшей частотой или вероятностью появления. В результате такого кодирования длина выходной кодовой последовательности становится короче относительно исходной [3, 10].

Однако использование таких методов перекодирования данных связано с необходимостью применения сложных алгоритмов обработки информации и большого количества вычислительных операций. В частности, один из наиболее эффективных методов – метод Хаффмана – предусматривает большой объем сортировок элементов массивов данных в процессе построения кодового дерева. Алгоритм Хаффмана математически гарантированно создает наименьший по размеру код для каждого из символов исходных данных и относится к классу алгоритмов оптимального префиксного кодирования. Классический алгоритм Хаффмана является статическим двухпроходным алгоритмом (первый цикл – накопление массива данных, вычисление вероятности или частоты появления каждого символа в массиве и сортировка данных, второй – построение кодового дерева и получение сокращенных кодов для каждого символа) [2, 4, 9]. С ростом количества элементов, входящих в обрабатываемый массив данных, в зависимости от используемого алгоритма сортировки время решения задачи растет с той или иной степенью нелинейности и в кон-

Методы обработки данных це концов становится неприемлемо большим для удовлетворительного решения задачи информационного обеспечения.

Таким образом, существует противоречие между возможностью использования метода Хаффмана для сокращения объемов передаваемых данных и ростом сложности его реализации при увеличении их разнообразия.

То есть задачей разработчика кодирующего устройства, реализующего преобразование данных методом Хаффмана (как и с помощью любого другого подобного метода экономного кодирования), является его модернизация с целью снижения влияния алгоритмов сортировки на время решения задачи при заданном количестве сортируемых элементов.

Постановка задачи модификации алгоритма реализации кодирования данных методом Хаффмана с целью сокращения количества выполняемых машинных операций

Метод Хаффмана относится к статистическим методам сжатия данных без потерь [4].

Подавляющий объем операций при реализации данного метода приходится на алгоритмы сортировки данных, которые, исходя из уровня сложности, можно разделить на два вида.

Первый вид – предварительная сортировка элементов исходного алфавита A { a_j } на начальном этапе реализации метода Хаффмана. Для удобства назовем ее « Сортировка 1 » . Она выполняется один раз, являясь при этом наиболее сложной и длительной по времени выполнения совокупностью операций, так как затрагивает все элементы множества A { a_j }. Ее задачей является расстановка элементов a_j в порядке возрастания их значений.

Вторая группа – сортировки, выполняемые в процессе построения кодового дерева и формирования таблицы соответствия. Задачей таких сортировок является определение позиции вновь полученного элемента a_j в текущем множестве A_M { a_j }. Это более быстрый вид сортировок, так как изначально все ^r элементы множества, кр ^r ом ^r е вновь полученного, уже упорядочены, решается задача поиска первого элемента, не превышающего заданный. Однако количество таких сортировок велико и имеет значение N – 1, где N – мощности исходного множества A { a_j }. Данный вид сортировок назовем «Сортировка 2».

Сложность алгоритма характеризуется двумя количественными показателями – емкостной и временной сложностью. Первый говорит о том, какой объем памяти, а второй – сколько времени необходимо для его выполнения [1, 8].

Говоря о емкостной сложности, имеют в виду количество памяти, необходимой для размещения всех данных, участвующих в вычислительном процессе: входные и выходные данные, промежуточные результаты. В большинстве случаев современная электронная база предоставляет разработчикам возможности, позволяющие считать память некритическим ресурсом, поэтому чаще всего под анализом сложности алгоритма понимают исследование его временнóй сложности.

Ясно, что одна и та же программа при одинаковых входных данных на разных вычислительных средствах будет в общем случае выполняться в течение разного времени [1, 8].

Поэтому под сравнительным анализом сложности алгоритмов будем понимать исследование того, как соотносится изменение времени работы программ при увеличении объема входных данных на гипотетическом вычислительном средстве с постоянными вычислительными характеристиками.

Реализация метода экономного кодирования Хаффмана ...

Временнýю сложность алгоритма выражают функцией Т ( n ) зависимости времени работы от размера входа. В задачах обработки одномерных массивов, коими являются задачи сортировки в нашем случае, под размером входа принято считать количество элементов в массиве.

Особенностью метода Хаффмана является то, что его временная сложность определяется не столько объемом входных данных n , сколько их разнообразием, то есть N количеством букв, составляющих алфавит входного массива, и необходимостью их сортировки. Поэтому в дальнейшем условимся использовать обозначение n , если речь идет о размерах входа алгоритма «в общем», и N , если говорится об алгоритме сортировки данных.

Таким образом, время выполнения алгоритма кодирования данных по методу Хаффмана можно представить как Т ( n , N ). Оно определяется суммой времени выполнения «Сортировки 1» – T ( N ), времени, необходимого на N – 1 сортировку вида «Сортировка 2» – ( N – 1) – T ( N ), времени, затрачиваемого на выполнение операций сложения при формировании узлов кодового дерева ( N –1) – T ( N ) – и времени T ( n ), затрачиваемого на представление исходного массива данных кодовыми последовательностями экономного кода:

T _алгор( n,N ) = T _Сорт1( N ) + ( N – 1) T _Сорт2( N ) + ( N – 1) T _сумм( N ) + T _кодир( n ). (1)

При этом T _кодир( n ) зависит от объема начальных данных n , представленных в равномерном коде, и для фиксированного объема n _фикс не зависит от методов, непосредственно используемых для решения задачи экономного кодирования. Соответственно, сократить Т _алгор( n , N ) при n _фикс = const возможно только за счет уменьшения величины остальных элементов выражения (1).

Так как мы определили, что сравнительный анализ алгоритмов выполняется на одном и том же оборудовании, время выполнения можно измерять в обычных единицах, кратных секунде. Однако в общем случае физическое время выполнения алгоритма – это величина τ∙ f , где f – число элементарных операций, реализованных в ходе выполнения алгоритма, а τ – среднее время выполнения одного элементарного действия. Число элементарных операций определяется структурой алгоритма, языком программирования и листингом программы и не зависит от схемной реализации ЭВМ, а среднее время выполнения – от скорости обработки сигналов компьютером. То есть алгоритм выполняется за конкретное количество действий – шагов. Поэтому объективной математической характеристикой временнóй сложности алгоритма является число элементарных действий, выполняемых в ходе работы алгоритма [1, 8].

Скорость выполнения алгоритма может существенно зависеть от содержания набора входных данных: время работы алгоритма в худшем и в лучшем случаях может сильно отличаться. Например, быстрая «в среднем» программа способна давать сбои в отдельных «плохих» случаях.

Оценка временной сложности алгоритма выполняется с использованием символа «О» (О большое). Формально O( f ( n )) означает, что время работы алгоритма растет в зависимости от объема входных данных не быстрее, чем некоторая константа, умноженная на f ( n ) – функцию, дающую верхнюю границу максимального числа основных операций, используемых алгоритмом при размере входных данных равном n .

Методы обработки данных

На рисунке 1 показаны графики роста О большого с увеличением количества информационных элементов на входе алгоритма в зависимости от вида функциональной зависимости О от n .

Ml о Sitz                    M2 ° sitact

	Si	s2	S3	s4
Oi		0,3		0,7
О2	0,2	0,5	0,3
Оз				1
04	0,1		0,9

	S1	S2	8з	S4
О1		0,3		0,7
02	0,2	0,5	0,3
Оз	0,2			0,8
04	0,1		0,9

Результирующая матрица М = М1*М2

I I ё< I ri I I ri I

Рис. 1 . Зависимость временной сложности алгоритмов от вида алгоритма сортировки данных

Известно достаточно большое количество методов сортировки. В таблице 1 приведены асимптотические оценки некоторых наиболее эффективных из них.

Таблица 1

Асимптотические оценки некоторых методов сортировки

Алгоритм	Временная сложность
	Лучшее	В среднем	В худшем
Быстрая сортировка	O( N log( N ))	O( N log( N ))	O( N 2 )
Сортировка слиянием	O( N log( N ))	O( N log( N ))	O( N log( N ))
Пирамидальная сортировка	O( N log( N ))	O( N log( N ))	O( N log( N ))
Блочная сортировка	O( Nk )	O( Nk )	O( N 2 )
Поразрядная сортировка	O( Nk )	O( Nk )	O( Nk )

Из таблицы следует, что наилучшими временными характеристиками располагает поразрядная сортировка. То есть верхняя граница максимального числа основных операций, реализуемых алгоритмом при размере входных данных, равном N , для данной сортировки не должна превышать Nk , где k – константа, характеризующая конкретный алгоритм.

Зависимость количества операций от N для поразрядной сортировки описывается законом, графическое представление которого на рисунке 1 имеет вид прямого луча. Константа k на рисунке является коэффициентом, определяющим угол наклона графика относительно оси N . Ее значение для конкретного алгоритма определяется количеством и разнообразием используемых в нем видов элементарных операций, а также структурой алгоритма.

При реализации в одних и тех же условиях двух алгоритмов с разными значениями k (одинаковые массивы входных данных, одинаковая схемная реализация ЭВМ) алгоритм с меньшим k дает выигрыш в количестве необходимых для его реализации элементарных операций (см. рис. 1, а ):

Реализация метода экономного кодирования Хаффмана ...

k ₁<  k ₂,

O₁( Nk ) < O₂( Nk ),                               (2)

n = соnst.

При этом с увеличением размера массива входных данных N выигрыш ∆O( Nk ) = = О_ПР( Nk ) – O₁( Nk ) линейно нарастает.

Для любого электронного вычислительного средства существует ОПР – максимальное количество элементарных операций, выполняемых данным средством в единицу времени.

На рисунке 1, б показано, что данному граничному значению для каждого выполняемого алгоритма соответствует свое предельное значение объема массива входных данных N _ПР, при этом с уменьшением характеризующего алгоритм значения k значение N _ПР возрастает. Иными словами, при одном и том же О_ПР предельное значение массива входных данных больше для алгоритма с меньшим значением k :

k ₁<  k ₂, N ПР1 >  N ПР2 , O = O_ПР.

Ясно, что если для решения какой-то задачи обработки данных необходимо использовать входной массив размером Nтребуемое, который окажется больше NПР, используемого для этого алгоритма, получить полный выходной массив данных за заданный промежуток времени не удастся.

Кроме того, известно [6], что если в классическом алгоритме Хаффмана сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм в целом будет работать за время O(NklogN). Вероятно, такую асимптотику можно улучшить до O(Nk), используя усовершенствованные методы сортировки.

Таким образом, сформулируем задачи, решаемые в данной работе.

• 1.    С целью повышения эффективности обработки данных в электронных вычислитель-

• ных средствах, в частности для уменьшения времени выполнения сортировок потока данных при реализации кодирования методом Хаффмана, предложить алгоритм сортировки c характеристикой временной сложности вида О(Nk) и коэффициентом kA алгоритма, меньшим чем kПС алгоритма поразрядной сортировки:

• 2.    Предложить механизм реализации метода Хаффмана, позволяющий снизить его временную сложность с вида O( Nk log N ) до вида O( Nk ).

J k _A<  k _ПС, I O < O_ПС.

Способ реализации экономного кодирования методом Хаффмана с использованием модифицированных алгоритмов сортировки данных

Основным недостатком всех алгоритмов сортировки, включая поразрядную сортировку, является необходимость в выполнении большого количества операций сравнения элементов обрабатываемого числового массива, а также операций смещения подмножеств элементов между ячейками памяти при освобождении выделенной под отсортированный элемент позиции. Минимизировав количество таких операций, можно получить алгоритм, свойства которого описывает система условий (4).

Методы обработки данных

В отличие от существующих алгоритмов сортировки предлагаемый алгоритм использует операции сравнения лишь в некоторых возникающих при особых условиях ситуациях. Кроме того, в нем минимизировано количество операций сдвига.

Идея сортировки, реализуемая данным алгоритмом, заключается в однопроходной последовательной замене элементами исходного массива элементов переходного массива, находящихся на позициях, соответствующих численному значению очередного выбранного элемента исходного массива с дальнейшим уплотнением переходного массива по- средством удаления оставшихся незамещенными элементов.

Реализация экономного кодирования методом Хаффмана включает в себя следующие шаги.

Шаг 1. Накопление информации в течение интервала наблюдения Т Н с целью получения статистик элементов U . , из которых формируется входной неупорядоченный массив данных M { m r } (рис. 4, а ).

Шаг 2. Формир > ование алфавита А { а . } конечной мощности N , каждому элементу а которого соответствует единственное значение U .

Шаг 3. «Сортировка 1» – упорядочивание элементов алфавита в порядке возрастания.

Шаг 4. Построение кодового дерева и формирование таблицы соответствия исходного и экономного двоичного кода алфавита.

M m } _Тн

Шаг 5. Представление элементов массива с помощью экономного кода.

Рассмотрим более подробно реализацию шага 3, предполагающую выполнение

«Сортировки 1», – упорядочивание элементов полученного алфавита в порядке возра- стания их значений. На данном этапе возможно значительное сокращение времени пе- рекодирования за счет отказа от использования традиционных алгоритмов сортировки данных.

Вместо реализации того или иного порядка последовательного взаимного сравнения элементов сортируемого массива предлагается алгоритм упорядочивания данных посредством занесения информации об анализируемых элементах в ячейки памяти, адреса которых соответствуют их абсолютной величине (рис. 2, а ). Назовем его модифицированным алгоритмом сортировки исходного массива.

При этом предполагается выполнение следующих этапов.

• 1.    Среди элементов А { a i } определяются значения с максимальной и минимальной частотой появления на Т Н - A max и A min , которые задают размер промежуточного массива:

  
  
  

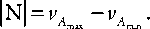
• 2.    В памяти вычислительного устройства резервируется последовательно адресуемый ряд ячеек, при этом адреса первой и последней ячеек данного ряда имеют, соответственно, значения и v_A + А № и v_A + А № , где А № - смещение относительно адресов ячеек, имеющих значения v_A и v_A .

• 3.    На завершающем этапе выполняется проход по элементам промежуточного массива Ν ^′{ν _j }. При этом формируется новый, конечный, массив данных Ν_K {ν _i }:

Последовательно от V 1 до v _N выполняется следующий проход по массиву N {v . }. При этом, так как все значения v . лежат внутри интервала [ v_A , v_A ], данные величины можно рассматривать как адреса ячеек выделенного участка памяти вычислительного устройства. То есть при наличии определенного числа в массиве N {v . } в соответствующую ячейку заносится «1». Если данное число встречается в массиве в нескольких позициях, то при

Реализация метода экономного кодирования Хаффмана ...

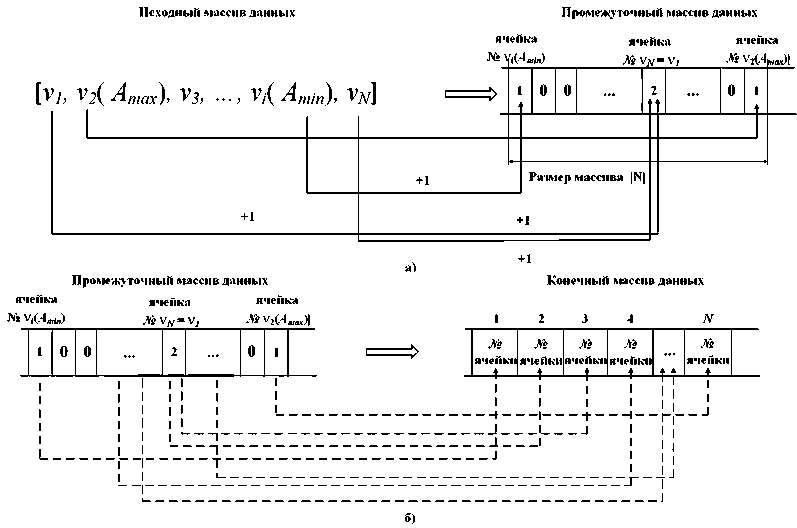
Рис. 2. Шаг 3: упорядочение исходного массива данных прохождении каждой такой позиции значение величины, хранящейся по заданному адресу, увеличивается на единицу. Таким образом формируется промежуточный массив данных Ν′{νj}, содержащий в определенных позициях информацию о количестве элементов массива Ν{νi} того или иного вида:

Ν {ν _i } → Ν ^′{ν _j }.

При этом возможна ситуация, когда часть ячеек останется незаполненной в связи с отсутствием в Ν {ν _i } элементов с соответствующим значением.

Ν ^′{ν _j } → Ν_K {ν _i }.

Формирование Ν_K {ν _i } происходит согласно следующему правилу (рис. 2, б ).

Просмотр элементов массива Ν ^′{ν _j } – ячеек выделенной памяти – выполняется от значения ячейки с адресом v_{A min} и далее – в сторону ячейки с адресом v_A . При этом в качестве очередного элемента Ν_K {ν _i } принимается значение адреса ячейки памяти, к которой выполняется обращение (с учетом смещения ∆№), при условии, что значение числа, хранящегося там, не равно нулю. Такие адреса игнорируются. Если содержимое ячейки превосходит по величине единицу, значение ее адреса последовательно заносится в Ν_K {ν _i } количество раз, равное значению содержимого данной ячейки. Таким образом, после опроса всех ячеек памяти, соответствующих Ν ^′{ν _j }, будет окончательно сформирован массив Ν_K {ν _i } мощностью N , идентичный по составу входящих в него элементов массиву

Методы обработки данных

Ν_K {ν _i }, но при этом структурно представляющий собою их неубывающую по величине последовательность.

Таким образом, для сортировки данных с помощью предложенного алгоритма достаточно выполнить три полных прохода по последовательности элементов сортируемого массива.

Шаг 4 включает построение кодового дерева и формирование таблицы соответствия исходного и экономного двоичного кода алфавита. При этом переход к нему возможен сразу после формирования промежуточного массива Ν ^′{ν _j }, так как дальнейшая часть общего алгоритма предполагает работу с входными данными именно такого формата. То есть количество проходов массива при выполнении «Сортировки 1» возможно уменьшить до двух.

Шаг 4 предполагает наличие «Сортировок 2». При этом вместо бинарного поиска предлагается использовать модернизированный алгоритм, позволяющий уменьшить количество элементарных операций, приходящихся на данный шаг.

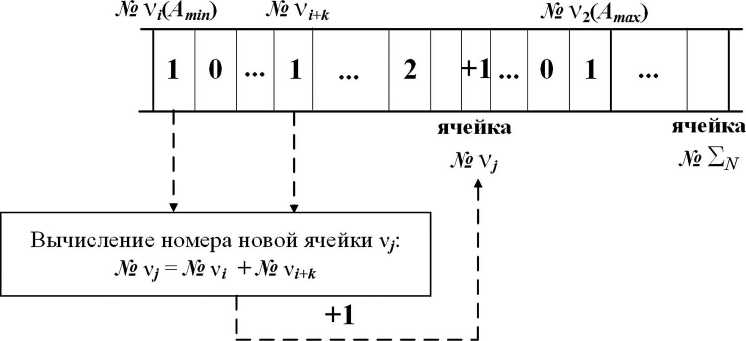
Как и в классическом методе Хаффмана, построение узлов кодового дерева начинается с суммирования частот первых двух элементов массива. Для этого в Ν ^′{ν _j } определяется значение числа, находящегося в первой позиции, – ячейке с адресом ν _i ( A _min), так как данная ячейка всегда заполнена. Если данное значение равно единице, то ищется следующая ячейка – ν _i+k , в которой содержится величина, отличная от нуля (рис. 3, а ). На основе суммы значений адресов данных ячеек формируется новый адрес ячейки, содержимое которой необходимо увеличить на единицу:

ν _j = ν _i + ν

i+k .

Это будет означать, что в новом массиве, который назовем трансформируемым массивом Ν ^′{ν _j }, вновь сформированный элемент помещается в соответствующей его частоте ν _i позиции. Верхняя граница данного массива ограничивается положением ячейки, адрес которой равен сумме значений всех входящих в него элементов Σ _N .

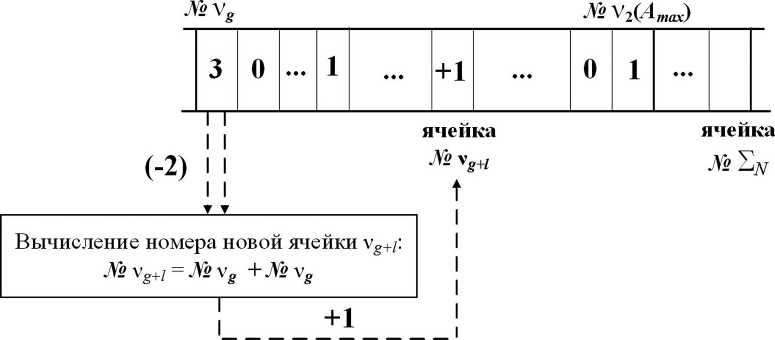
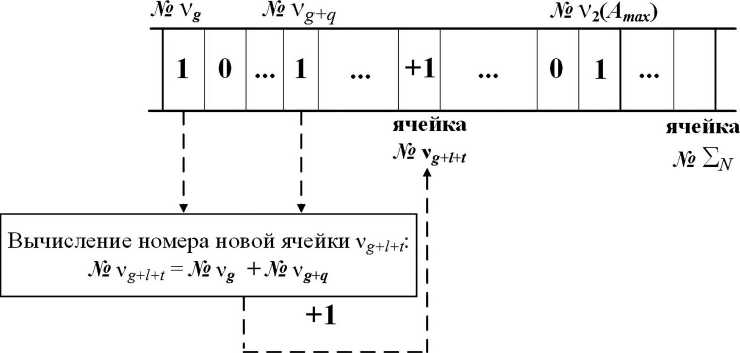
Случай, когда ячейка содержит число, значение которого превышает единицу, эквивалентен наличию соответствующего количества одинаковых членов ряда. При этом построение очередного узла дерева выполняется суммированием двух значений адреса данной ячейки с уменьшением хранящегося в ней числа на две единицы (рис. 3, б, в):

ν _g+l = ν _g + ν _g .

Процесс построения узлов кодового дерева сопровождается построением двоичных кодовых последовательностей для участвующих в нем элементов исходного массива Ν ^′ _T {ν _j }с последующим формированием таблицы соответствия кодовых алфавитов.

На последнем этапе кодирования данных (шаг 5) выполняется представление элементов массива M { m r } с помощью полученных двоичных последовательностей экономного кода и формирование выходного информационного потока.

Реализация метода экономного кодирования Хаффмана ...

Промежуточный массив данных ячейка ячейка                 ячейка

а)

Трансформируемый массив данных ячейка                            ячейка

б^

Трансформируемый массив данных ячейка ячейка                  ячейка

в)

Рис. 3. Шаг 4: построение кодового дерева

Методы обработки данных

Оценка эффективности модифицированных алгоритмов сортировки данных

Реализация метода Хаффмана состоит из нескольких этапов, содержащих сортировки вида «Сортировка 1» и «Сортировка 2». При этом наиболее подходящим известным алгоритмом для реализации первого из них является поразрядная сортировка, обеспечивающая наибольшую эффективность при практической реализации метода, для второго – бинарный поиск.

Анализ временной сложности предложенного алгоритма реализации этапа «Сортировка 1» и алгоритма поразрядной сортировки показывает, что оба они выполняются за линейное время и имеют нотацию О большое вида O( Nk ). Понятно, что относительная сложность алгоритмов определяется соотношением соответствующих значений k .

В основе поразрядной сортировки лежит принцип разделения чисел упорядочиваемого ряда на массивы, содержащие числа с одинаковыми значениями в разрядах с совпадающими весами [5]. Обычно сортировку начинают с проверки крайних – младших или старших – разрядов и движутся затем, соответственно, в направлении возрастания или уменьшения их номеров. При этом на упорядочивание ряда по текущему разряду достаточно одного цикла-прохода по его элементам – они распределяются по группам, в которые входят числа с одинаковыми значениями в рассматриваемом в данном цикле разряде. Соответственно, для полной сортировки необходимое количество циклов совпадает с разрядностью сортируемых чисел p : ряд, состоящий из одноразрядных чисел, будет разделен на соответствующие подмножества за один проход, состоящий из двухразрядных – за два, и так далее. При этом значение O( Nk ) растет как с увеличением N , так и пропорционально росту количества разрядов p . То есть по сути в данном случае p = k .

Модифицированный алгоритм сортировки исходного массива выполняется за три прохода независимо от того, числа какой разрядности сортируются, а при реализации метода Хаффмана с использованием модернизированного алгоритма поиска, как было показано, необходимость в третьем цикле вообще отпадает. Уже при пороговом значении k _ПС = 3 предлагаемый алгоритм начинает выигрывать у алгоритма поразрядной сортировки в количестве необходимых элементарных операций, и с ростом p эта разница приобретает кратные значения (рис. 4 и табл. 2).

Таблица 2

Кратность значений с ростом p

p	1	2	3	8	16
k ПС / k A	1/3(2)	2/3(2)	3/3(2)	8/3(2)	16/3(2)

Данные о времени, затрачиваемом предлагаемым алгоритмом на решение задачи сортировки в зависимости от объема сортируемого массива, приведены в таблице 3 и на рисунке 5. Видно, что связь между количеством элементов в массиве и временем вычислений практически линейна (нелинейность графику придает необходимость сокращения длины горизонтальной оси), а его наклон имеет незначительный угол, что указывает на малую скорость нарастания времени обработки с ростом объема сортируемых данных.

Реализация метода экономного кодирования Хаффмана ...

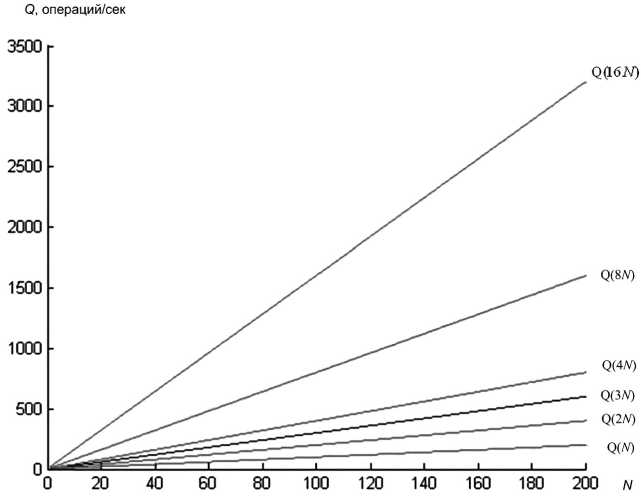
Рис. 4. Зависимость количества элементарных операций от N и p , необходимых для реализации алгоритмов сортировки

Таблица 3

Решение задачи сортировки в зависимости от объема материала

Кол-во элементов в массиве	500	1000	2000	4000	8000	16000	32000
Время вычисления, с	0,0195	0,51	0,57	0,61	0,75	1,09	2,06

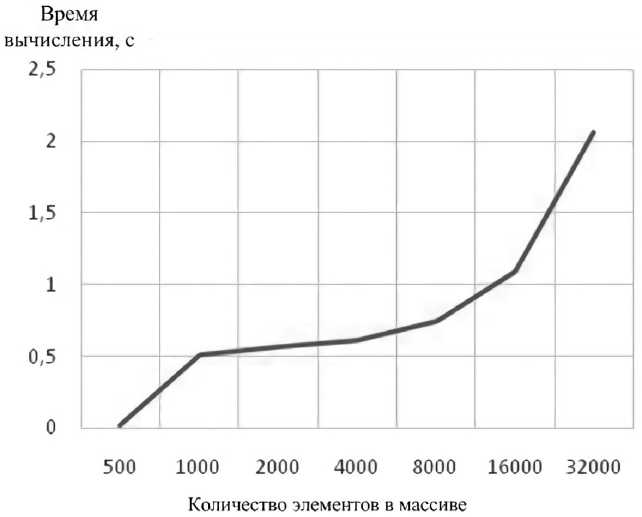
Рис. 5. Зависимость времени выполнения сортировки от объема массива

Для сравнения в таблице 4 приведены результаты моделирования для метода сортировки «пузырьками».

Методы обработки данных

Таблица 4

Метод сортировки «пузырьками»

Кол-во элементов в массиве	10	50	100	150	200	250	350	500	1000	2000
Время вычисления, с	0,0033	0,044	0,277	0,765	1,69	3,20	8,24	22,9	172,0	1348,2

В данном случае количество элементов массива менялось внутри небольшого диапазона – от 10 до 2000 чисел, что связано с экспоненциальным характером анализируемой зависимости: если при минимальном количестве элементов А время вычисления составляло тысячные доли секунды, то при 200 элементах на вычисление затрачивалось в среднем около полутора секунд, при 2000 элементах на упорядочивание массива требовалось более 22 минут.

Результаты работы алгоритма ускоренной сортировки отличаются от вышеприведенных кардинально: при объеме входных данных в 500 элементов они сравнимы с результатами выполнения сортировки «пузырьками» лишь для 50 входных значений, а с ростом размера входного массива относительный рост эффективности предлагаемого метода только увеличивается. Так, 2000 элементов с его помощью обрабатываются в среднем за 0,57–0,6 секунды (для метода «пузырьков» этому объему соответствует значение в 22 минуты), а на 32000 элементов необходимо всего 2 секунды.

Таким образом, эффективность алгоритма ускоренной сортировки можно было бы считать доказанной, однако разработанный алгоритм имеет некоторые особенности, ограничивающие его применение при определенных условиях.

В таблице 5 и на рисунке 6 приведены результаты эксперимента, в котором исследовалась зависимость t _вычисл( А ) с учетом значений абсолютной величины m наибольшего члена входного массива.

Величина наибольшего мента в массиве

Рис. 6. Зависимость времени выполнения сортировки от объема массива и значения его наибольшего элемента

Таблица 5

Результаты эксперимента

Кол-во элементов в массиве		500	1000	2000	4000
Величина наибольшего элемента в массиве / время вычисления, с	6000	0,0282	0,037	0,062	0,123
	10000	0,053	0,065	0,089	0,145
	20000	0,174	0,182	0,215	0,295
	30000	0,425	0,43	0,475	0,531

Реализация метода экономного кодирования Хаффмана ...

Очевидно, что с ростом m время выполнения сортировки растет, причем динамика процесса незначительно отличается от линейной. Это связано с тем, что с ростом m растет диапазон просматриваемой алгоритмом памяти, ограниченный значениями максимального и минимального элементов А , несмотря на независимость количества прохождений по массиву при сортировке от значений A и m .

В заключение отметим особенности реализации этапа «Сортировка 2». При использовании бинарного поиска, сложность которого имеет вид О(log N ), часть алгоритма Хаффмана, реализующая построение кодового дерева, имеет сложность О( N log N ). В то же время модернизированный алгоритм поиска позволяет решить задачу кодирования всего лишь за один проход, то есть имеет сложность О( N ).

Заключение

Таким образом, предложенный подход к решению задачи кодирования позволяет значительно снизить уровень противоречий между эффективностью метода Хаффмана по сокращению больших объемов данных и ростом сложности его реализации при увеличении их разнообразия, снижая влияние алгоритмов сортировки и поиска на время решения задачи при заданном количестве сортируемых элементов. При этом временная сложность модифицированного алгоритмом сортировки исходного массива составляет O(3 N ), что при количестве разрядов в сортируемых числах более четырех позволяет считать его наиболее быстрым из известных алгоритмов сортировки. При совместном его использовании с модифицированным алгоритмом поиска в кодере Хаффмана его временная сложность составит O(2 N ). При этом временную сложность алгоритма самого метода Хаффмана удается снизить с вида O( Nk log N ) до вида O( Nk ) .