Реализация метода Рунге - Кутты для решения оду с разрывной правой частью

Вводные замечания

Специалистами, занимающимися разрывными системами, было предложено трактовать дифференциальные уравнения (ДУ) с разрывной правой частью как уравнения с многозначной правой частью или дифференциальные включения [7]. В настоящее время такой подход к определению решений разрывных систем является наиболее употребительным, и не удивительно, почему начало интенсивного развития теории дифференциальных включений, теории ДУ с разрывной правой частью и теории автоматического регулирования совпадают по времени.

Одно из направлений исследования систем ДУ с разрывной правой частью обосновано в работах М.А. Айзермана и Е.С. Пятницкого [2]. Это направление условно назвали физическим в отличие от математического направления, развитого, в частности, в работах А.Ф. Филиппова [6].

Из анализа работ, посвященных различным методам исследования качественного поведения разрывных систем, следует отметить еще один содержательный и общий метод эквивалентного управления, получивший развитие в работах В.И. Уткина [7].

Численное решение дифференциальных уравнений

Киричевский Ростислав Викторович кандидат технических наук, доцент, доцент кафедры пожарной безопасности Института гражданской защиты Луганского государственного университета имени Владимира Даля. Сфера научных интересов: математическое моделирование, численные методы, программные комплексы, САПР в механике эластомеров. Автор 70 опубликованных научных работ.

Начало систематического изучения разрывных систем относится к 60-м гг. XX в. в связи с возникновением и развитием теории автоматического регулирования. В настоящее время существуют такие системы релейного действия, в которых хотя бы в одном звене при непрерывном изменении входной величины в некоторых точках процесса выходная величина изменяется скачкообразно. Такое звено называется релейным, где статическая характеристика имеет точки разрыва. Для определения этих характеристик используется ДУ с разрывной правой частью.

Дадим обзор некоторых подходов к решению таких уравнений. По теореме Пеано, задача Коши y' = f(x, y), y(x0) = x0                                    (1)

локально разрешима в случае непрерывной функции f(x , y ). Иначе утверждение теоремы Пеано в общем случае неверно [3]. Если функция f(x , y ) удовлетворяет определенным условиям – имеет разрыв по у или является кусочно-непрерывной по х – подходы к решению ОДУ предлагаются в научной литературе [7, 9]. Иногда используют известные численные методы, меняя сетку разбиения при подходе к точке разрыва, значение функции в этой точке доопределяют по А.Ф. Филиппову [6]. Однако общего алгоритма для построения сетки не предложено.

Для устранения разрыва 1-го рода по х Л. Лопесом и Н. Буоно предложен подход, который заключается в решении уравнения [9]

k -1

У.+1( oh) = y. + h E Yj (°)A 7 f - j •                                 , j=0

где σ ∈ (0; 1), γ_j ( σ ) – коэффициенты, взятые из метода Адамса – Башфорта, h – шаг, Δ f_{i -1} = f_t – f_{i –1} , Δ ² f_{i– 2} = f_i – 2 f_{i– 1} + f_{i– 2} ,... - конечные разности. Для 4-го порядка точности имеем:

Реализация метода Рунге-Кутты для решения ОДУ с разрывной правой частью

У+J '-) = y. + h I A0f л + A1f,-1 ^- + A2f,-2I    +^- | + к                2 v 64

x

)

+A3 f     +—+   + A4 f      + — ++ —

3 к 24   6   6 )        к 120  16   728

Однако для решения ОДУ с разрывом 2-го рода такой подход не работает.

А.Ф. Филипповым разработаны мощные инструменты для анализа существования решений ОДУ и систем ДУ с разрывом. Однако подходы к численному решению ОДУ, если f(x , y ) имеет разрыв 2-го рода по х , не представлены в открытом доступе.

Предложим подход к решению ОДУ с разрывной правой частью по х методом Рунге – Кутты со специально подобранным шагом в окрестности точки разрыва.

Описание предложенного подхода

Для численного решения (1) применим метод Рунге – Кутты в случаях, когда f(x , y ) имеет вид дробно-рациональной, -иррациональной, -обратной тригонометрической функции, то есть имеет разрыв 2-го рода по х . В качестве расчетных формул применим [2]:

yi +1= yi + Δyi где

A y _t = 1( k ( ¹ ) + 2 k 2 ' ) + 2 k 3 ' ) + k 4 ) ), 6

^k 1 i ) = ^hf ( xi > yi ),

k ⁽ i ) = hf f x- + ~, У- +    ^,

• 2 J(i 2X 2 у

• (i)    / h k(i))

k 3 =hf ^ xi+2, yi+у, k 4 i) = hf (Xi + h, yi + k(i)), хi = х0 + ih, yi = у(хi) (i = 0,1,2,...), h – шаг.

Отметим, что для явных методов Рунге – Кутты 4-го порядка радиус области абсолютной устойчивости, если правая часть ОДУ удовлетворяет условию Липшица, определяется равенством

2      3      4

R ( z ) = 1 + z + — + — + — + O ( z ⁵), 2!   3!   4!

которое следует из того, что e^λу является точным решением задачи у' = λf ( х , у ), у ₀ = 1, и из равенств у_{п +1} = R(λh)у_п , e^z – R ( z ) = O ( z ⁵). Выбор параметров выражения (4) можно проводить не только из условия минимальной локальной погрешности, но и из расширения области устойчивости (для ОДУ с разрывом 2-го рода в правой части, исключая точки разрыва).

Численное решение дифференциальных уравнений

Проверим различные варианты при подходе к точке разрыва: за один шаг интервал разбиения уменьшим на 20, 50 и 80%. Затем после «перескока» точки разрыва пересчет осуществим уже с обычным шагом. В случае поиска решения при наличии одной точки разрыва наилучшие решения в сравнении с точными решениями (абсолютные погрешности минимальны) дал вариант: к точке x_{i –1} , предшествующей точке разрыва x_i , добавим 0,2 h , при этом в формулах (4) для точек x_{i –1} , x_i , x_{i +1} шаг остается 0,2 h . В точке разрыва решение доопределим значением, следующим сразу за точкой разрыва.

Применение предложенного подхода, когда нет точного решения, предлагаем с использованием правила Рунге: формулы для оценки погрешности решения ОДУ методом Рунге – Кутты

I y 2 i ⁽ h ) - y, ⁽² h )|

2 p - 1

< £ ,

где р – порядок метода Рунге –Кутты, в нашем случае p = 4, ε – заданная точность. То есть для обеспечения требуемой точности применим выбор шага методом двойного просчета, чтобы для каждой точки численного решения значения отличались на величину, не превышающую заданной погрешности.

Нетрудно показать, что погрешность этого метода на каждом шаге есть величина порядка h ⁵ в предложении, что f(x , у ) ∈ C ₅ ( G ), где G – область, на которой отыскивается решение задачи Коши.

Ниже приведено несколько примеров, иллюстрирующих точность, предложенного подхода.

Численный пример 1

Рассмотрим решение задачи Коши

У' =-1-, y(0)=0,

1 — 2 x на отрезке [0;3], приняв шаг h = 0,05 и h = 0,025 [1–8].

Задача (6) представляет собой ОДУ с разделяющимися переменными. Его решение y = –0,5ln 1 – 2x легко получается интегрированием правой части. Правая часть (6) f (x y ) =—— имеет разрыв 2-го рода в точке x = 0,5, не является кусочно-непрерывной и 1 - 2 x удовлетворяет условиям Каратеодори [7]: 1) f (х, у) непрерывна почти ∀ x, 2) множество точек разрыва правой части имеет нулевую меру Лебега, 3) существует локально суммируемая функция m : R → R такая, что при каждом фиксированном у почти ∀ x выполняется неравенство f(х, у) ≤ т(х).

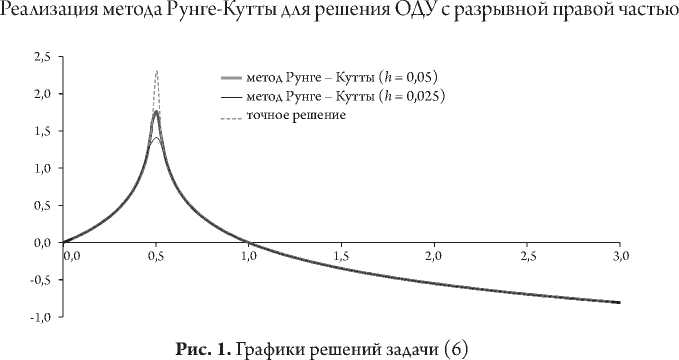
Кривые решений задачи (6) представлены на рисунке 1: точного, с шагом 0,025 и 0,05 методом Рунге – Кутты. Решения методом Рунге – Кутты, полученные при уменьшении сетки разбиения в два раза, дали абсолютные погрешности вычислений минимум в 3,9 раза меньше, кроме точки, ближайшей к разрыву, хотя на рисунке 1

этого не заметно.

Численный пример 2

Рассмотрим решение задачи Коши у'П—, у(0) D0 ,                            (7)

x 1

на отрезке [0;3], приняв шаг h = 0,05 и h = 0,025.

ДУ задачи (7) аналогично (6). Его численное решение также можно сравнить с точным. Различие заключается в выпуклости решения. Кривые решений задачи (7) представлены на рисунке 2: точного, с шагом 0,025 и 0,05 методом Рунге – Кутты. Решение методом Рунге – Кутты, полученное при уменьшении сетки разбиения в два раза, даже на графике (рис. 2) заметно ближе к точному. Максимальная абсолютная погрешность после точки разрыва с шагом 0,025 составила 0,03939.

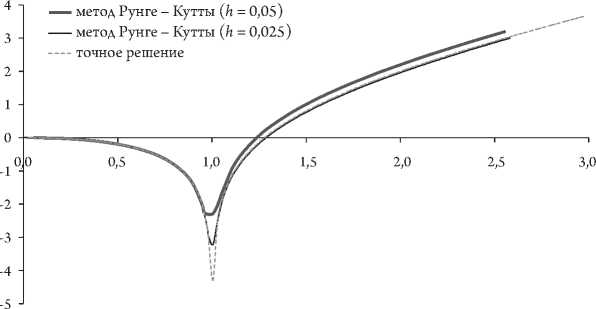
Рис. 2. Графики решений задачи (7)

Численный пример 3

Рассмотрим решение задачи Коши

У* = _П-----x ------, У (0) = 0,                             (8)

--arcsin(2 x ) 4

на отрезке [0;0,5], приняв шаг h = 0,005 и h = 0,01.

Численное решение дифференциальных уравнений

Задача представляет собой ОДУ с разделяющимися переменными. Правая часть (8) 2

имеет разрыв 2-го рода в точке x =---® 0,353553, не является кусочно-непрерывной, удовлетворяет условиям Каратеодори. Точного решения нет, поскольку интеграл от пра-

вой части не выражается через элементарные функции, но представляет собой при под-

становке sin x =

e

it

—

e

— it

2 i

интегральную экспоненту.

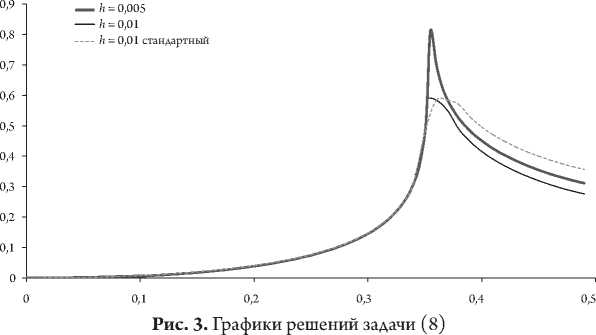
На рисунке 3 представлены решения задачи (8) при h = 0,01 стандартным методом

Рунге – Кутты и по предложенному подходу с измененной сеткой разбиения при h = 0,01 и h = 0,005 методом Рунге – Кутты. К концу интервала абсолютная погрешность между

решением с шагом 0,005 и решениями с шагом 0,01 увеличилась на 0,0714 при применении стандартного метода Рунге – Кутты.

Заключение

В работе проанализированы решения задачи Коши на примерах ОДУ первого порядка с разрывом 2-го рода в правой части на предмет сходимости численного решения в окрестности точки разрыва и после нее: использование метода Рунге – Кутты с измененной сеткой и коэффициентами в окрестности точки разрыва целесообразно. При этом в формулах (4) для точек x_{i –1} , x_i , x_{i +1} шаг равен 0,2 h , поскольку он дал наилучшие решения в сравнении с точными решениями (абсолютные погрешности минимальны), в точке разрыва решение доопределяется значением, следующим сразу за точкой разрыва. Предложенная схема изменения шага сетки представлена на рисунке 4.

x x x точка x x i -2 i -1 i                      i +1 i +2

разрыва

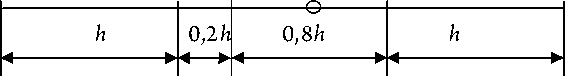
Рис. 4. Схема изменения шага

Реализация метода Рунге-Кутты для решения ОДУ с разрывной правой частью