Реализация параллельных вычислений при разностном решении уравнений математической физики

Решение разностных уравнений требует больших временных затрат, которые иногда становятся неприемлемыми в силу срочности задачи или ограниченности доступа к вычислительной технике. Поэтому актуальна проблема построения алгоритмов, обеспечивающих поддержку параллельных вычислений и тем самым позволяющих ускорить вычисления .

В ИСОИ РАН установлен кластер, составленный из четырех двухпроцессорных компьютеров Pentium 2, с оперативной памятью 512 Мб каждый и тактовой частотой 400 МГц и 450 МГц (по два компьютера соответственно), соединенных сетью со скоростью 100Мбит. При данной конфигурации целесообразно нагружать один процессор не более, чем одним процессом и пользоваться разделенной памятью, когда процессу соответствует область памяти, которой никакой другой процесс пользоваться не может. Взаимодействие между процессами осуществляется пересылкой данных.

Разностные схемы, применяемые для решения временных задач математической физики, по способу определения искомой функции на некотором временном слое делятся на явные [1] (функция определяется через значения на предыдущем временном слое) и неявные (функция определяется через значения на текущем временном слое). Также авторы рассматривают явно-неявные схемы для решения систем дифференциаль ных уравнений, когда значение одной из искомых функций определяется через значения других искомых функций как явно, так и неявно.

Распараллеливание явной схемы

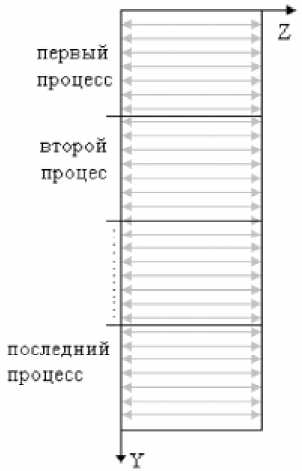
В качестве примера распараллеливания явной схемы рассмотрим схему, составленную для решения уравнения теплопроводности [1], записанного в одномерной декартовой системе координат. В качестве характеристик такой схемы можно отметить явность, одномерность, отсутствие времени ожидания процессами результатов работы других процессов и малые вычислительные затраты. При распараллеливании авторы использовали очевидный метод распределения сеточной области по процессам (рис.1), при котором каждому процессу отводится своя часть сетки по направлению оси Z.

Нахождение очередной строки сетки (временной слой) происходит в два этапа: сначала процессы обмениваются значениями в крайних узлах своей области сетки (рис.1) с соседними процессами, а затем вычисляют значения в узлах следующей строки.

В примере использовалась область с первый        второй процесс         процесс последний

процесс

Z

Вычисление значений температуры на временном шаге T+A t

Рис. 1. Реализация явной схемы.

Т - текущее время, DDt - шаг по времени

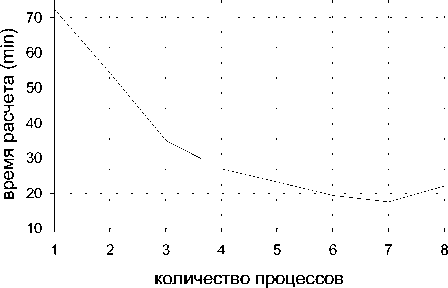
Рис. 2. Зависимость времени работы программы от числа процессов для явной разностной схемы

где T1- время работы программы без распараллеливания (один процесс), TN- время работы параллельной программы с числом процессов равным N.

Некоторые авторы вводят эффективность как [3]

n=t— вычислений

t вычислений

+      + t обмена простоя

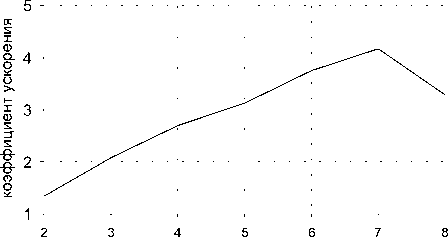
количество параллельных процессов

Рис. 3. Зависимость ускорения программы от числа процессов для явной разностной схемы

где tвычислений - время, которое программа потратила на вычисления, 1обмена - время, которое программа потратила на обмен данными между процессами и 1простоя - время, которое программа ожидала.

Однако учитывая, что t вычислений

N а           вычислений t обмена

T1

N

⁺ t простоя , ^легко

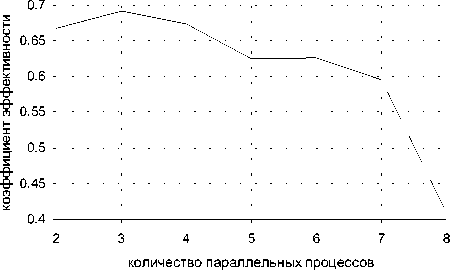
Рис. 4. Зависимость эффективности программы от числа процессов для явной разностной схемы

приходим к формулам (1), (2). Учитывая сложность работы кластера и невозможность точного определения времени обмена и времени ожидания, авторы предпочитают для определения эффективности использовать формулы (1) и (2).

По рис.3 видно, что ускорение при увеличении числа процессов имеет линейный характер до некоторого предела. Из этого можно сделать вывод о том, что несмотря на минимальное количество передаваемых данных и отсутствие времени простоя, нельзя добиться большего ускорения при увеличении числа процессов начиная с семи.

Существенным недостатком явной схемы является ограничение на шаг дискретизации. Часто таких недостатков лишены неявные схемы.

N z =1512000. Результаты работы представлены на рис.2-4:

Коэффициент ускорения вычисляется как [3]

k

T1

ускорения

T n ,

а коэффициент эффективности

k

к ускорения

эффективности

N

Распараллеливание явно-неявной схемы

При распараллеливании явно-неявных схем, построенных для решения системы уравнений Максвелла, авторы применяли известный алгоритм реализации продольнопоперечных прогонок [4], в котором использовали только продольные прогонки. Продольной считалась та прогонка, для реализации которой необходим один процесс. Для реализации поперечной прогонки необходи-

1      2      3      4      5      6      7      8

количество процессов

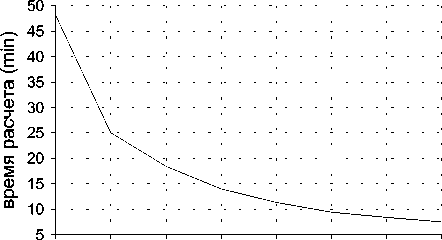
Рис. 7. Зависимость времени работы программы от числа процессов для явно-неявной разностной схемы

числа процессов. Это говорит о том, что можно добиться большей эффективности, увеличивая число процессов.

Рис. 5. Разбиение сеточной области при N z y мо задействовать все процессы.

Схемы явно-неявного характера позволяют для нахождения напряженности электрического поля ограничиться только продольной прогонкой. Это является их преимуществом перед неявными схемами. Если сеточная область не квадратная, то появляется свобода в выборе способа распределения памяти при распараллеливании задачи. Так, для минимизации размера пересылаемых данных, а значит и времени пересылок, для количества точек сетки Nz по направлению Z и Ny по направлению Y при Nz меньше Ny целесообразно разбивать сеточную область на части по направлению Y (рис.5). А при Nz больше Ny целесообразно разбивать сеточную область на части по направлению Z (рис.6).

В качестве примера рассмотрим область, в которой Ny=25, Nz=15120. Используем разбиение по сеточной области, представленное на рис.6.

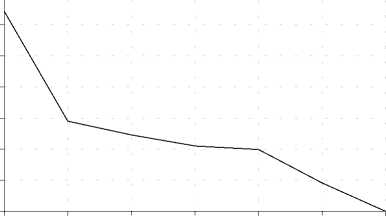
По рис.7-9 можно заключить о линейном характере ускорения при увеличении

Распараллеливание неявной схемы

Однако при решении разностных схем переменных направлений не избежать поперечной прогонки. Известная конвейерная схема поперечной прогонки [4] реализуется синхронным алгоритмом распараллеливания с применением правой прогонки. Авторы предлагают использовать асинхронный алгоритм с применением как правой так и левой прогонок [5].

Представим сеточную область в виде строк и столбцов, где каждый процесс будет работать с определенным количеством столбцов. Для четной строки первый процесс будет заканчивать прямой ход левой прогонки и начинать обратный, для нечетной строки последний процесс будет заканчивать прямой ход правой прогонки и начинать обратный ход. Для нечетной строки первый процесс будет начинать прямой ход правой прогонки,

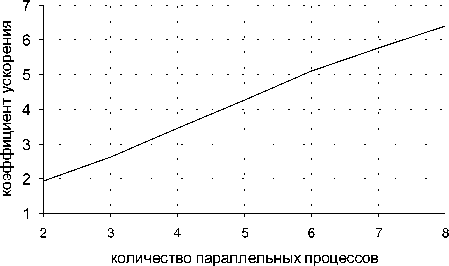
Рис. 8. Зависимость ускорения программы от числа процессов для явно-неявной разностной схемы о 0.95

| 0.925

0.9

| 0.85

0.825

0.8

2        3        4        5        6        7        8

количество параллельных процессов

Рис. 9. Зависимость эффективности программы от числа процессов для явно-неявной разностной схемы

для четной строки последний процесс будет начинать прямой ход левой прогонки. Центральные процессы в зависимости от четности строки и ее положения (верхняя обрабатываемая или нижняя) будут продолжать прямой и обратный ход левой и правой прогонок.

Так как объем вычислений и передаваемых данных для синхронного и асинхронного алгоритма будет одинаков, то различие в их эффективности будет определяться различием во времени ожидания. Время ожидания алгоритма будет равно времени ожидания любого процесса (в случае гомогенного кластера). Для синхронного алгоритма время ожидания:

‘„^„‘(N-Wl+yTN-1) (‘з+‘4). (4) где t1 - время прямого хода прогонки, t3 - время обратного хода прогонки, t2 - время передачи коэффициентов прогонки, t4 - время передачи искомой функции (в предположении, что передача и прием происходят одновременно).

Время ожидания асинхронного алгоритма в случае, когда число строк четно, составит:

t задержки

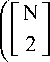
1 Ь + t₂ ) +

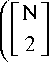
⁺ t 4 ) , (5)

где операция [..] есть округление до ближай шего целого.

Таким образом время ожидания асинхронного алгоритма будет меньше, чем у синхронного. Если число строк много больше количества процессов, разница по времени исполнения программ, реализующих пред-

Рис. 10. Разбиение сеточной области для минимизации пересылок в случае неявной схемы

ставленные алгоритмы будет почти незаметной, однако при малом числе строк разница весьма существенна. Например для двух процессов, работающих с сеткой из четырех строк, в пренебрежении временем пересылки по формуле (3) эффективность синхронного алгоритма составит 2/3, а эффективность асинхронного 1.

При реализации алгоритма решения разностных уравнений неявных схем [6], построенных для решения уравнений Максвелла, с целью минимизации времени обмена данными необходимо разбить сеточную область таким образом, чтобы вектор поперечной прогонки по размеру превосходил вектор продольной прогонки (рис.10).

Для примера, приведенного в предыдущем пункте, представим результаты работы программы, реализующей асинхронный алгоритм.

В отличие от аналогичных результатов предыдущего пункта ускорение и эффективность значительно ниже, что связано с увеличением объема пересылок в три раза и необходимостью тратить время на ожидание. Однако кривые ускорения и эффективности не

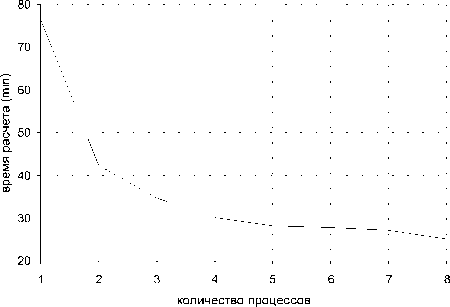
Рис. 11. Зависимость времени работы программы от числа процессов для неявной схемы

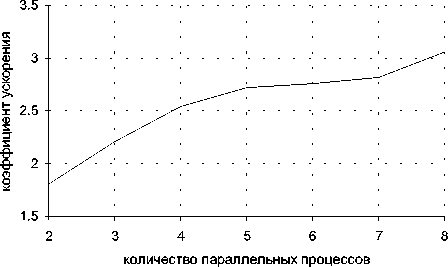
Рис. 12. Зависимость ускорения программы от числа процессов для неявной схемы

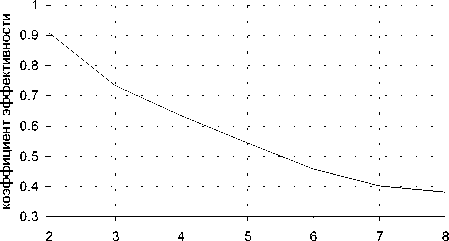
количество параллельных процессов

Рис. 13. Зависимость эффективности программы от числа процессов для неявной схемы

стогнируют, что позволит добиться лучшего ускорения при увеличении числа процессов.

Заключение

Повышение эффективности распараллеливания происходит при сокращении объема данных, передаваемых между процессами, и времени ожидания при том же объеме вычислений. Для минимизации объема передаваемых данных следует разбивать сеточную область таким образом, чтобы граница разбиения содержала как можно меньше узлов сетки. Время ожидания можно сократить, применяя предложенный асинхронный алгоритм реализации поперечной прогонки, использующий правую и левую прогонки одновременно.