Реализация приемной антенны на механизме электрокинетического явления "потенциал течения"

В работах [1, 2] начат цикл статей (целый ряд из которых находится в печати), описывающих физические модели для реализации излучателя нового вида, основанного на использовании такого процесса электрокинетических явлений (ЭЯ), как электроосмос. В этом цикле будут описаны физические процессы, проясняющие принцип действия этого излучателя. Вместе с тем в ЭЯ существует процесс, обратный электроосмосу, носящий название потенциала течения . В настоящей работе рассматривается возможность использования процесса потенциала течения для обращения излучателя в приемную акустическую антенну.

ПОСТАНОВКА ПРОБЛЕМЫ

С целью возможности обращения излучающей акустической антенны, работающей на основе процесса электроосмоса, в приемную акустическую антенну необходимо описать математическую модель процесса с использованием такого обратного к электроосмосу феномена ЭЯ, как потенциал течения.

РЕШЕНИЕ ПРОБЛЕМЫ

Потенциал течения

Вначале дадим некоторые формулировки [3, с. 534]. ЭЯ — совокупность явлений, происходящих в системах, содержащих капилляры или мембраны, размещенные в электролите, при наложении электрического поля, и обратных к ним эф- фектов. К ЭЯ относятся: электроосмос, потенциал течения, электрофорез и эффект Дорна. Здесь остановимся на двух ЭЯ: явлении электроосмоса и обратном ему явлении — потенциале течения.

Электроосмос — течение жидкости в капиллярах или пористых телах под воздействием внешнего электрического поля; потенциалом течения называется появление электрической разности потенциалов на торцах капилляра или мембраны при течении через них жидкости.

Таким образом, в электроосмосе источником движения жидкости является приложенное к ней внешнее электрическое поле.

Потенциал течения (протекания) — это явление возникновения разности потенциалов при перемещении дисперсионной среды через капиллярно-пористую перегородку. Таким образом, в потенциале течения источником возникновения электрического поля является движение самой жидкости.

Для описания этого явления приведем некоторые сведения. Основную роль в ЭЯ играют двойной электрический слой (ДЭС), формирующийся на границе раздела фаз, и его поляризация. Внешнее электрическое поле, направленное вдоль границы раздела фаз, смещает один из ионных слоев ДЭС по отношению к другому. Это приводит к относительному перемещению фаз — к электроосмосу (и к электрофорезу). При относительном движении фаз, вызываемом внешним механическим воздействием, происходит перемещение ионных слоев ДЭС — пространственное разделение зарядов, т.е. возникает разность потенциалов. Потенциал течения рассматривается на примере проницаемой мембраны, разделяющей резервуары с электролитом при наличии перепада давления и, следовательно, течения электролита через мембрану [3, с. 534]. Часть ионов одного знака диффузной части ДЭС увлекается течением жидкости, что приводит к появлению разности потенциалов между резервуарами и вызывает появление электрического тока в направлении, противоположном конвективному переносу заряда. Поскольку этот ток возникает в отсутствие перепада потенциала под влиянием движения жидкости, его обычно называют током течения и обозначают istr . Разность потенциалов, установившаяся при компенсации этих токов называется потенциалом течения. Подробнее см. [4, § 2.5].

В работах [4–7] и ряде других работ приводится выражение, связывающее потенциал течения Аф с величиной перепада давления A p . Однако вследствие отличий приведенных там выражений этой зависимости, в настоящей работе приводится подробный его вывод, основанный на материалах работы [5, § 15.11.4] (где в итоге приведено неверное выражение), описывающих зависимость потенциала течения от перепада давления.

Выражение для потенциала течения

Вывод зависимости потенциала течения от перепада давления приводим, следуя работе [5, § 15.11.4], где эта зависимость получена с помощью аппарата неравновесной термодинамики. Согласно этому подходу, электроосмос и потенциал течения описываются уравнениями термодинамики неравно в есных процессов. Средние скорость жидкости V , п роходящей через мембрану, и плотность тока i (записываем эти векторные величины в виде единственных, отличных от нуля проекций) по сечению мембраны связаны с перепадом давления A p и перепадом потенциала на торцах мембраны А ф феноменологическим соотношением неравновесной термодинамики [5, § 15.11.4]

V — Л11Аp + Л12 Аф, i — Л 21 Ap + Л22Аф,

где кинетические коэффициенты Л 11 , Л ₁₂, Л ₂₁, Л 22 характеризуют соответственно гидродинамическую проницаемость мембраны, скорость осмотического течения, ток течения и электропроводность электролита. Кинетические коэффициенты удовлетворяют соотношениям Онзагера (теорема Онзагера)

Л 12 =Л 21 ,                      (2)

а вся система (1) является линейной относительно перепада давления Ap и потенциала течения Аф. Величины Аp и Аф здесь принимаются постоянными.

Найдем последовательно величины Л _у (далее везде используется система СИ). Скорость осмотического течения V_{e 0} в капилляре при условии a » A D , где a — радиус капилляра, а A D — длина Дебая (примерно равная толщине ДЭС) практически во всем сечении капилляра равна [8, с. 159]

V. 0 = ^-Е — - ^ZАф .         (3)

η      ηl

Здесь

E -?.

где E

амплитуда вектора

электрической напряженности E , приложенной к жидкости; l — длина капилляра.

Сравнение (1) и (3) дает

εε0ζ

—--

η l

Согласно соотношению Онзагера (2), сразу получаем

Л 21

εε0ζ

—--

η l

Для средней скорости V _P ламинарного течения в трубке (течение Пуазейля) имеем [9, § 17]

V p —    А p .                  (6)

8 η l

Из сравнения (1) и (6) получаем

Л„ —

. 8 η l

Наконец, из второго уравнения (1) получаем, что средняя плотность тока, вызванная потенциалом течения, равна

σ istr — ОЕ — - у Аф , где σ — удельная проводимость жидкости. Отсюда и из второго уравнения (1) имеем

Л 22 —

σ

. l

По определению, потенциал течения Аф находится из условия равенства нулю средней плотности тока i — 0. Тогда из второго уравнения (1) получаем условие для определения потенциала течения i = Л21Аp + Л22Аф = 0. (9) Подставляя в (9) выражения (5) и (8), окончательно получаем для потенциала течения

Аф = -^21Ap = - ssoZ Ap. (10) Л 22 pa

С поправкой на то, что (10) приведено в системе СИ, оно совпадает с точностью до знака, например, с выражением (1.2) в [4, с. 10] или с выражением (IV.16) в [7, с. 184], но не совпадает, как отмечено выше, с выражением (15.112) в работе [5, с. 516], где, по-видимому, присутствует опечатка.

Соотношение (10) показывает, что потенциал течения не зависит от площади сечения капилляра, а задается только величиной перепада давления. Этот результат подтвержден в многочисленных экспериментах для самых многообразных мембран [5, с. 516].

На рисунке (заимствован рисунок 15.12 из [5, с. 516]) представлена зависимость потенциала течения от перепада давления для кварцевого капилляра радиусом 10 мкм при течении через него 1-1 электролита с концентрацией 10–2 моль/л. Видно, что величина потенциала течения может иметь достаточно большое значение.

При переходе от индивидуального капилляра к реальной связнодисперсной системе (мембрана или диафрагма) возникают усложнения, связанные со структурой порового пространства, в котором происходит перенос вещества и электрического тока. Однако все описанные закономерности типа (1)–(10) остаются справедливыми, и в этом случае только радиус капилляра и его длина заменяются некоторыми размерными коэффициентами, называемыми структурными факторами [7, с. 184].

В проведенных выше рассуждениях принима-

Δ φ , В

240 - лось, что величины Аф и Ap имеют постоянные значения. Однако в капиллярах, в частности, и в капиллярно-пористых структурах, в целом, величины Аф и Ap могут быть переменными по сечению капилляра. Тогда, как видно из цепочки рассуждений (1)–(10) (в этом случае система (1) ос-редняется по сечению капилляра, а кинетические коэффициенты Л11, Л12, Л21, Л22 уже изначально усреднены), выражение (10) верно и для средних по сечению значений Аф и Ap

Аф = - ££oZ Ap. (10а) ησ

Кроме того, полученные результаты можно попытаться обобщить на случай переменных во времени величин А ф ( t ) и A p ( t ) при условии, что время релаксации зарядов в жидкости^* много меньше периодов колебаний величин ф ( t ) и p ( t ) . Тогда выражение (10) можно переписать в следующем виде

Аф(t) = -^^Ap(t). (11) ησ

Преобразуем (11) в дифференциальную форму. Помножим обе части (11) на - p e / 1 . Имеем (зависимость от времени t опускаем для краткости)

Аф    ss0Z Ap

—Pe — = Pe--Г l      ησ l

.

Свяжем выражения (11), (12) с такими величинами, как вектор напряженности электрического поля и градиент давления. При 1 = A z ^ 0 имеем из (12):

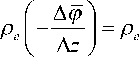
ss 0 Z A p П^ A z

f дф )    ss0Z dpI ' 1 = p

V дz J     n^ дz

Обозначим E = -V ф — среднее по сечению капилляра значение вектора электрической напряженности, соответствующего потенциалу сечения. С учетом допущения E = ( 0,0, E ) из цепочки (13) получаем:

Δ Р , МПа

Зависимость потенциала течения от перепада давления ( [5, с. 516] )

P e E = P e ^ V p .          (14)

ησ

Таким образом, в рамках принятых предположений при проведенных выше выкладках получено, что объемная электрическая сила в уравнении Навье—Стокса ρeE (см. [1, 2, 4–6, 11, 12] и др.), действующая при электроосмосе, эквивалентна εεζ объемной силе pe —— Vp, действующей при по-ησ тенциале течения.

В случае гармонического процесса с циклической частотой ω выражение (14) переписывается в виде

P e E ( to ) = P e ^ V p ( to ) .            (15)

ησ

Здесь под E и p принимаются модули гармонических величин E e ^{to t} и pe ^to" .

Таким образом, в случае потенциала течения возникает действующая на жидкость средняя объ-εεζ емная сила Pe —— Vp, которая эквивалентна ησ средней объемной силе ρeE , характерной для процесса электроосмоса, где E — среднее по сечению капилляра значение вектора напряженности электрического поля, отвечающего потенциалу течения. Это позволяет воспользоваться полной системой уравнений электрогидродинамики [12], представленной усеченно, например, в работах [1, 2, 4–6, 8, 11].

Система уравнений для потенциала течения

Для темы настоящей работы существенным является только уравнение Навье — Стокса (сохранения импульса). Как и в [1, 2, 11, 12], принимаем его в наиболее общем виде для движения вязкой сжимаемой однородной жидкости:

d v_

P —- + (P ’V) v\ = dt    V ’ n A

= ^V p _Z ⁺ П ^АР ⁺ I ^{Z +} J l^VV' v , ⁺ P el E g ⁺ F . ⁽¹⁶⁾

Здесь P^= Pg + P, vE = Vg + v, pE = pg + p — соответственно поля плотности, скорости и давления в жидкости; Eg = const — вектор напряженности внешнего электрического поля; F — внешняя объемная сила, являющаяся источником процесса потенциала течения; ζ — объемная вязкость. Ин- декс 0 соответствует электроосмотическому процессу, источником которого является электрическое поле E0 ; величины без индекса соответствуют процессу потенциала течения, вызванного силой F (весьма упрощенный вариант такой модели использовался ранее в [6, § 63] при совместном математическом моделировании электроосмоса и потенциала течения).

Подставим в (16) значения суммарных полей. Далее примем, что течение в электроосмотическом процессе ламинарное. Тогда уравнение (16) применительно к стационарному электроосмотическому процессу в несжимаемой жидкости с учетом V p _g = g (см., например [1, 11]) принимает вид

P g ( v g "^V ) v g = n ^{A v} g ⁺ P ei E g

V- V g = g.

Здесь полагается, что градиент равновесного давления V p _g равен нулю V p _g = g.

Акустический процесс (потенциал течения естественно представить как акустический процесс) рассматривается для сжимаемой жидкости в линеаризованном виде, и уравнение сохранения импульса для него получается подстановкой разложений P ^ = P g + P , V _S= V g + V , p _S= p g + p в (16) и вычитанием из него (17):

P g I    ⁺ ( v g ’^V ) ^{v +} ( ^v ’^V ) v g 1 =

Idtу

= -Vp + nAv + ^ Z + П ^VV-v + F.(18)

К уравнению движения (18) следует добавить стандартное линеаризованное уравнение непрерывности для сжимаемой жидкости:

^dP + PgV-v = g.(19)

Согласно (14) и (15), имеем соответственно

F (t ) = PeE (t ) = Pe nZ Vp (t) ,(2D)

F ( to ) = Pe E (to ) = Pe ^^gZ Vp (to ) .(21)

ησ

Подставляя в (18) вместо F его значение из (2g) в виде P _e E ( t ) мы по сути дела сводим задачу потенциала течения к линейной акустической электроосмотической задаче:

( dv /     .        / . A

P g I ^7 ⁺ ( v g ’^V ) ^{v +} ( ^v ’^V ) v g 1 =

Id t                      )

= -Vp + nAv + ^Z + nJVV-v + peE(t) , (22)

где p e E ( t ) определяется из (20).

Уравнение (22) содержит неопределенность, т.к. правая часть (22) содержит осредненное по сечению значение давления p искомого акустического давления p (см. (20)). Однако здесь речь идет не об определении параметров течения v , v ₀ и p (они полагаются известными), а о возможности решения обратной задачи, т.е. возможности замера величины вектора напряженности E ( t ) , вызванного потенциалом течения и напрямую связанного с акустическим полем ( v , p ) . Таким образом, уравнение (22) демонстрирует физическую модель процесса использования электроосмотического преобразователя в режиме приемника акустических колебаний.

Замечание

В (22) в отличие от [1, (6)] не пренебрегаем конвективным членом слева, т.е. полагаем, что число Рейнольдса электроосмотического течения v ₀ не пренебрежимо мало. Как будет показано в следующих работах, это позволяет получать некоторые качественные отличия по сравнению со случаем, когда электроосмотическое течение отсутствует v ₀ = 0 .

ВЫВОДЫ

В работе показано, что наличие обратимости двух электрокинетических явлений: электроосмоса и потенциала течения, позволяет использовать один и тот же преобразователь, основанный на наличии в капиллярно-пористых структурах развитого двойного электрического слоя, и как излучатель, и как приемник акустических колебаний. Эта обратимость выражена в работе путем записи уравнения Навье — Стокса для случая потенциала течения для акустических колебаний (приемник), которое оказалось эквивалентным аналогичному уравнению для случая электроосмоса (излучатель).

Работа выполнена в ИАП РАН в рамках Государственного задания 075-00780-19-00 по теме № 0074-20190013 Министерства науки и высшего образования.