Реализация радиационно-стойкого кодирования в рамках межкристальной связи систем, состоящих из нескольких программируемых интегральных схем

Для реализации алгоритмов управления космическими аппаратами (КА) универсальным решением являются программируемые логические интегральные схемы (ПЛИС) [1, 2].

Круг задач, возлагаемых на системы управления КА, с каждым годом расширяется. Реализуемые алгоритмы на сегодняшний день должны не только выполнять свои задачи, но и осуществлять защиту своей физической реализации от радиационных сбоев, а также иметь средства самоконтроля. Поэтому для реализации таких сложных систем требуются ПЛИС, имеющие большой запас логической емкости и большое количество портов ввода–вывода.

У разработчиков возникают трудности в реализации требуемых алгоритмов из-за ограниченного выбора производителей компонентной базы в условиях импортозамещения, так как ПЛИС российского производства имеют скромный объем логических элементов [3, 4] и крайне ограниченный перечень доступных корпусов.

Для этой цели нужен новый подход в проектировании алгоритмически сложных систем на базе ПЛИС, который должен учитывать требования к аппаратуре, специфику ее применения и ограничения по компонентной базе.

архитектура многокристальной системы и многопоточной межкристальной связи

Одним из вариантов решения сформулированной проблемы является разделение алгоритма управления на несколько ПЛИС, однако оно возможно только с учетом их функциональных особенностей. Наиболее распространенной задачей для систем управления КА является реализация многоканальных алгоритмов управления. Оптимальное решение задачи разделения функционала системы представлено на рис. 1. Данная архитектура подразумевает наличие базовой и N локальных ПЛИС. Базовая ПЛИС реализует алгоритмы, общие для всех объектов управления, а также интерфейсную часть. Каждая локальная ПЛИС на основе информации от базовой ПЛИС и сигналов обратной связи реализует индивидуальные алгоритмы для каждого объекта управления.

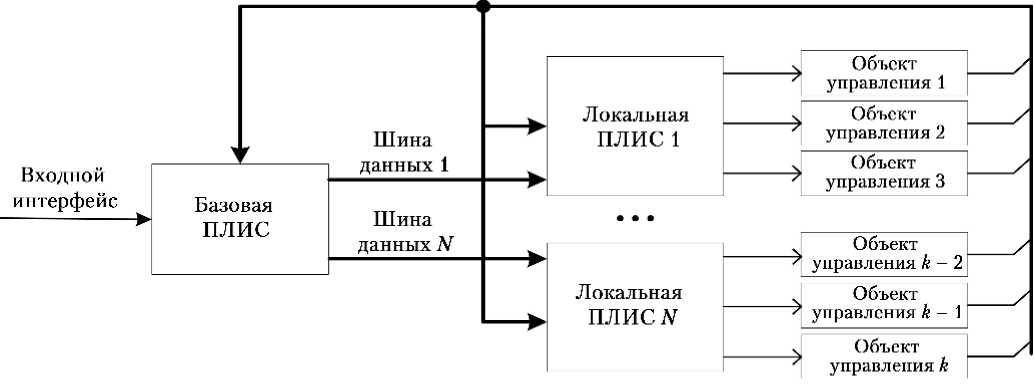
Рис. 1. Структурная схема многопоточной архитектуры межкристальной связи

Для передачи исходного сообщения длиной k ₀ символов от базовой ПЛИС к локальным может быть использован или любой из интерфейсов, или параллельная шина. Бóльшая часть реализуемых на ПЛИС интерфейсов обладает временнóй задержкой, не позволяющей обмениваться информацией на едином функциональном уровне, а параллельная шина позволяет элементам системы функционировать на одной частоте с задержкой, равной времени распространения сигнала между ними. Такой подход также дает возможность разрабатывать все ПЛИС как единое функциональное устройство, в котором базовые и локальные ПЛИС являются законченными IP -блоками, позволяющими реализовывать систему как на базе N + 1 ПЛИС, так и в одном кристалле. Данный подход позволяет при расширении номенклатуры элементной базы российского производства без изменений интегрировать всю систему в новую ПЛИС.

Одним из условий реализации подобной схемы является защита каждой линии шин данных посредством реализации кодирования, восстанавливающего ошибки [5], так как именно на основе информации, передаваемой по ним, будет формироваться управляющий сигнал для объектов управления.

Выбор метода защиты каналов, а именно, типа кодов, восстанавливающих ошибки, возлагается на разработчика системы и зависит от множества факторов, в частности, от методов кодирования, заложенных в других микросхемах, наработок в данной области команды разработчиков, специфики передаваемых данных и многих других. В данной работе будет рассмотрена защита с помощью сверточного кодирования, так как оно является наиболее подходящим для блокового кода [6].

Базовым элементом сверточных кодера и декодера является структура, хранящая значения одного символа m из k0 символов входного сообщения в течение n0 тактов. В отличие от классической реализации кодера на базе сдвигового регистра, в данной работе рассматривается реализация на циклически перезаписываемом регистре, представленном на рис. 2. Основная идея в том, что на каждом следующем такте запись производится в новый бит, а при переполнении регистра происходит перезапись наиболее старых записей [7]. При этом циклически перезаписываемый регистр H(m) для n0 = 3 во время тактов tn будет содержать следующие значения:

t ₁ : H ( m_i ) = ( m_i, m_{i –2} , m_{i –1} ) — сбоя нет;

• t ₂ : H ( m_{i +1} ) = ( m ^– _i, m_{i +1} , m_{i –1} ) — сбой в первом бите m ^– _i ;

• t ₃ : H ( m_{i +2} ) = ( m_i, m_{i +1} , m_{i +2} ) — перезапись бита не производилась.

Кодовые слова G ( H ( m )) из данных значений регистра будут следующими:

• t ₁ : G ( H ( m_i )) = ( ⊕ ₂ ( m_i, m_{i –2} ), ⊕ ₂ ( m_i, m_{i –1} ), ^⊕ 2 ^{( m} i –1 ^{, m} i –2 ^));

• t ₂ : G ( H ( m_{i +1} )) = ( ⊕ ₂ ( m ^– _i , m_{i +1} ), ⊕ ₂ ( m ^– _i , m_{i –1} ), ^⊕ 2 ^{( m} i +1 ^{, m} i –1 ^));

• t ₃ : G ( H ( m_{i +2} )) = ( ⊕ ₂ ( m_i, m_{i +1} ), ⊕ ₂ ( m_i, m_{i +2} ), ⊕ ₂ ( m_{i +1} , m_{i +2} )).

Как видно, в третьем такте за счет отсутствия перезаписи может быть восстановлен любой из сбоев, вызванный следующими эффектами [8, 9]:

• •    SET ( Single Event Transients ) — переходная ионизационная реакция;

• •    SEU ( Single Event Upsets ) — однократный восстанавливаемый сбой.

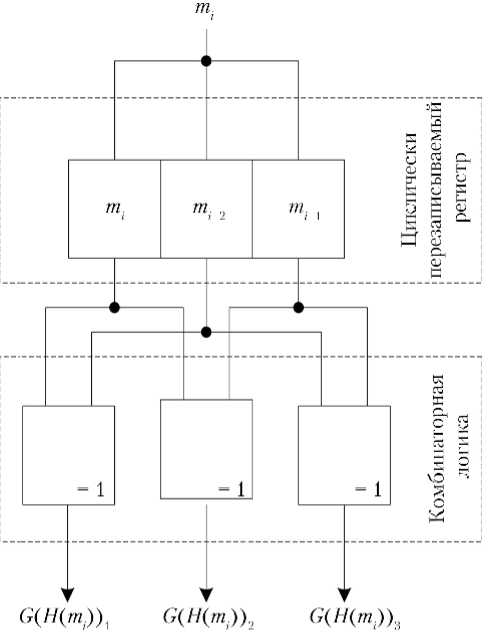
Рис. 2. Структурная схема линии связи с применением сверточного кодирования

Для реализации циклически перезаписываемого регистра необходимо реализовать счетчик, представленный на рис. 3, для выдачи адреса A = ( a ₁ , …, a_T ), несущего номер модифицируемого разряда регистра H ( m ).

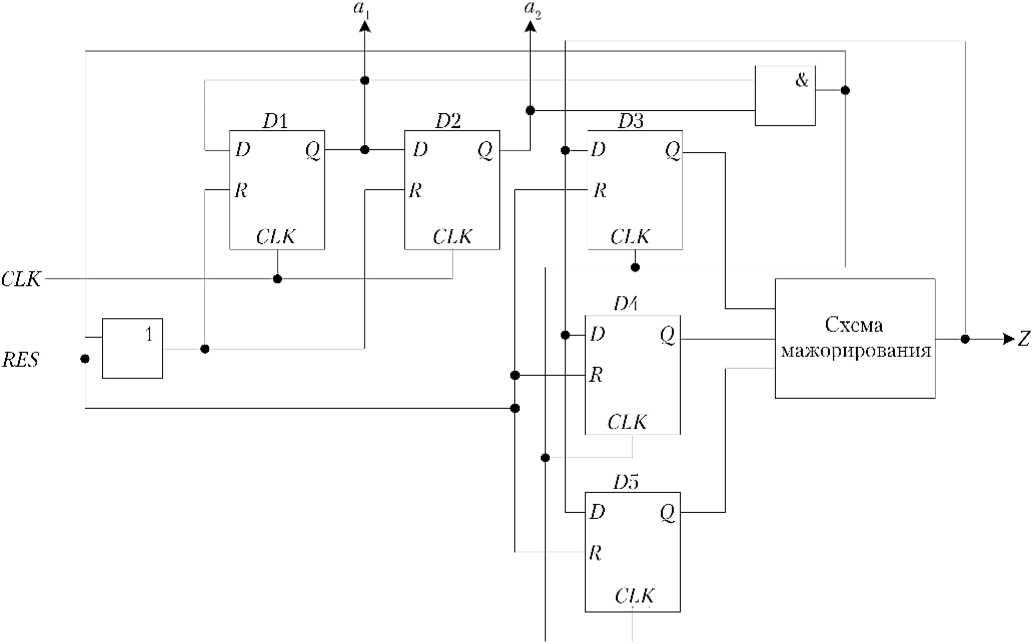
Рис. 3. Схема реализации счетчика адреса

Счетчик будет реализовываться на регистре длиной T разрядов при условии, что T = log ₂ n ₀ , и значение T округлено до целого значения в бóльшую сторону. В частности, для n ₀ = 3 необходимо реализовать счетчик, представленный на рис. 3, на двух триггерах D 1 и D 2, а для ограничения счета адресами 0, 1 и 2 — дополнительный сигнал сброса при a ₁ = 1 и a ₂ = 1 с помощью элемента конъюнкции, и произвести сброс счетчика или по данному сигналу, или по сигналу внешнего синхронного сброса.

На основе данной схемы был составлен перечень всех возможных критических сбоев, представленный в табл. 1.

Исходя из анализа данных табл. 1, было предложено не реализовывать схему защиты счетчика, а ввести дополнительный избыточный символ, формируемый по детерминированному алгоритму, и кодировать его аналогично символам исходного сообщения. Данный подход позволит на этапе декодирования восстанавливать значение адреса с учетом сбоя и на его основе проводить декодирование символов исходного сообщения.

Одним из вариантов формирования избыточного символа является схема, представленная на рис. 3, состоящая из триггеров D 3– D 5 и схемы мажорирования. По своей сути она является одноразрядным счетчиком, защищенным от сбоев троированием, для которого тактовым сигналом является сигнал сброса счетчика адреса. Схема защиты является обязательным условием, так как восстановление адреса декодером возможно только при условии достоверности избыточного символа.

Таблица 1

вероятные сбои в счетчике адреса

Начальное значение	01	10	00
Без сбоя	at 0 = 01 → at 0+1 = 10	at 0 = 10 → at 0+1 = 00	at 0 = 00 → at 0+1 = 01
Сбой в a 1	a t 0 = 01 → a t 0+1 = 01	a t 0 = 10 → a t 0+1 = 01	a t 0 = 00 → a t 0+1 = 10
Сбой в a 2	at 0 = 01 → at 0+1 = 01	at 0 = 10 → at 0+1 = 01	at 0 = 00 → at 0+1 = 00

В табл. 2 представлен полный перечень возможных кодовых слов на основе избыточного символа Z = 1 под действием внешних сбоев. Если расписать также все состояния для исходного избыточного символа Z = 0, то станет видно, что сбои в счетчике адреса и соответствующие им выходные кодовые слова полностью совпадают с расписанными в табл. 2, однако состояние циклически перезаписываемого регистра будет инвертированным.

При декодировании последовательности кодовых слов, сформированных на основе избыточного символа Z в условиях радиационного защелкивания (эффект SEL — Single Event Latchup ) бита циклически перезаписываемого регистра, они могут совпасть со словами, сформированными при сбое схемы счетчика адреса, и решение будет неоднозначным, поэтому была реализована схема кодирования, представленная на рис. 4.

Данная схема на каждом такте записывает c помощью дешифратора значение избыточного символа Z параллельно в оба циклически перезаписываемых регистра по адресу a . Далее дешифратор формирует на входе комбинаторной логики значение одного из регистров, в зависимости от сигнала С меняющего свое состояние с частотой, равной половине тактовой частоты. Таким образом, исключается возможность формирования двух последовательных недостоверных кодовых слов G в результате радиационного защелкивания.

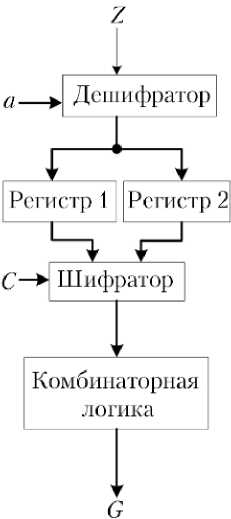
Рис. 4. Схема кодирования избыточного символа Z

Суммируя все доработки, радиационностойкий кодер для межкристальной связи ПЛИС выполняется в соответствии со схемой базовой ПЛИС, представленной на рис. 5.

Как видно из схемы, представленной на рис. 5, сообщение, сформированное универсальным алгоритмом управления, разбивается на k ₀ символов. К исходному сообщению добавляется избыточный символ Z , формируемый на основе генерируемого на каждом такте адреса A . Все k ₀₊₁ символов записываются в соответствующие им циклически перезаписываемые регистры, входящие в состав

Таблица 2

вероятные выходные кодовые слова на основе избыточного символа при ошибках в адресе

Начальное значение	00				01				10
Сигналы	A	Z	H	G	A	Z	H	G	A	Z	H	G
Без сбоя	00	1	001	011	01	1	011	110	10	1	111	000
	01	1	011	110	10	1	111	000	00	0	110	011
	10	1	111	000	00	0	110	011	01	0	100	110
Сбой в a 1	0 0	1	001	011	0 1	1	011	011	1 0	1	111	000
	10	1	101	101	01	1	011	011	01	0	101	101
	00	0	100	110	10	1	111	000	10	0	001	011
Сбой в a 2	0 0	1	001	011	0 1	1	011	110	1 0	1	111	000
	00	0	000	000	01	0	001	011	01	1	111	000
	01	0	000	000	10	0	001	011	10	1	111	000

сверточного кодера, по установленному для данного такта адресу. Из каждого регистра комбинаторной логикой формируется выходное кодовое слово, которое поступает на передатчик кодового слова и передается в декодер. Кодовое слово G ( H ( Z )), сформированное из избыточного символа, поступает параллельно на все локальные ПЛИС, а кодовые слова из информационных символов G ( H ( m_i )) разделяются на группы в зависимости от того, к какому объекту управления они относятся.

Декодирование начинается с анализа кодовых слов G'_Z , сформированных на основе избыточного символа, из которых восстанавливаются достоверные адреса A , и только после этого на их основе параллельно декодируют все k ₀ кодовых слов из символов исходного сообщения. Алгоритм декодирования слов G'_Z строится по принципу конечного автомата, граф которого представлен на рис. 6. Переход к новому состоянию осуществляется на каждом такте по алгоритму, индивидуальному для каждого состояния.

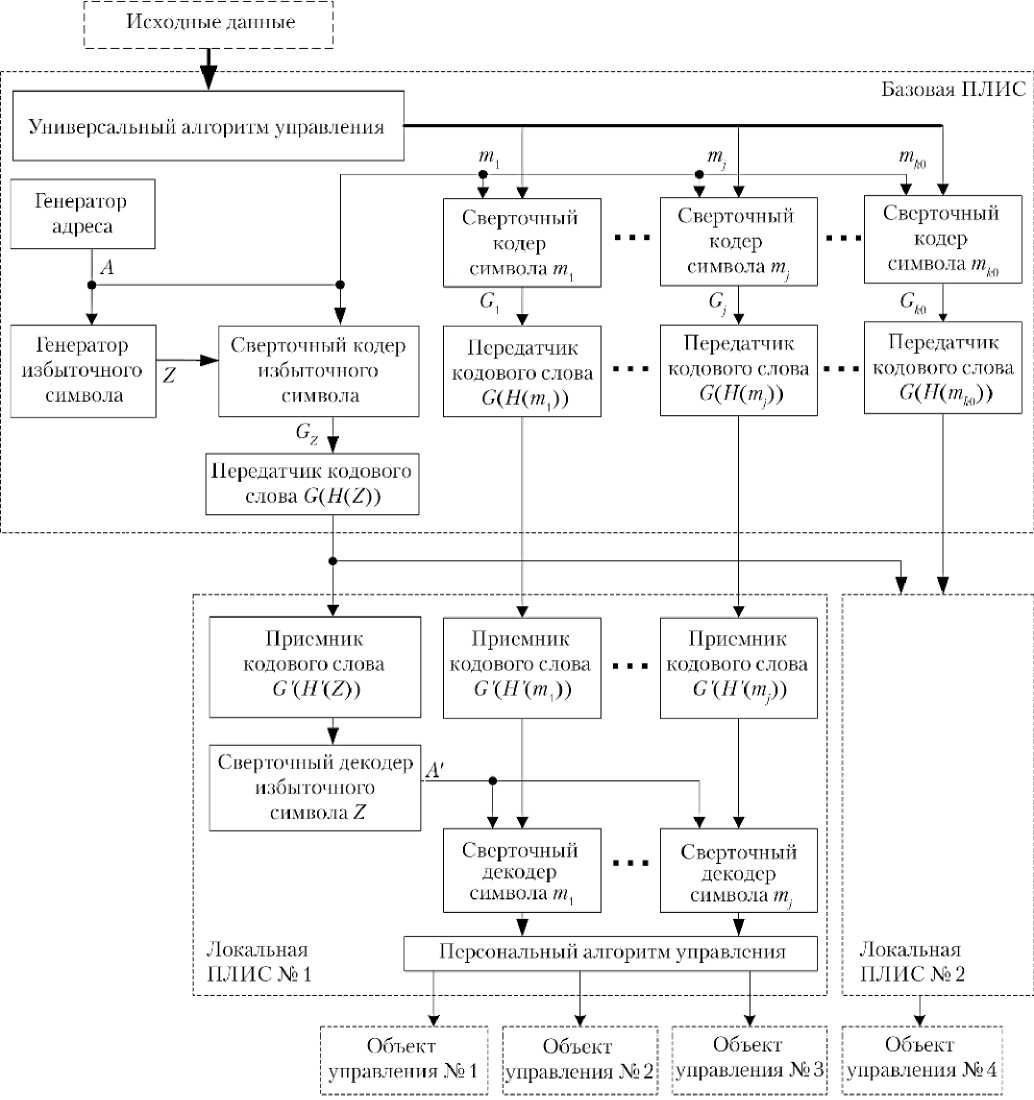
Рис. 5. Функциональная схема сверточных кодера и декодера

В соответствии с рис. 6 восстановление достоверного значения адреса, т. е. переход к состоянию «0», происходит с максимальной задержкой в два такта. Поэтому в декодере реализуется сдвиговый регистр из трех переменных B ₁ , B ₂ и B ₃ , хранящих состояния адреса во время тактов t ₀ , t ₀₊₁ и t ₀₊₂ . На каждом такте, независимо от состояния конечного автомата, происходит запись B ₁ в B ₂ и B ₂ в B ₃ параллельно с выводом нового значения А ₁ в адресную шину для сверточных декодеров каждого символа исходного сообщения. Количество записанных новых значений в переменные B ₁ , B ₂ и B ₃ может варьироваться в зависимости от состояния конечного автомата в настоящем такте.

Восстановление достоверного адреса производится на основе сохраненных на предыдущем такте значений адреса и циклически перезаписываемого регистра Н'_Z . Основным состоянием декодера является состояние «0», логика перехода из которого описывается алгоритмом, представленным на рис. 7. В основе перехода из состояния «0» лежит модифицированный алгоритм Витерби [10], суть которого для данной задачи сводится к перебору всех возможных модификаций Н'_Z , при условии принятия достоверным значения адреса, и формированию кодовых слов G'_{Z 1} и G'_{Z 0} длиной n ₀ символов путем n ₀ линейных комбинаций разрядов модифицированных регистров

Н'_{Z 1} и Н'_{Z 0} . Как видно из блок-схемы, представленной на рис. 7, необходимо произвести расчет расстояний Хемминга d ( G' ( H ( Z )), G'_{Z 1} ) и d ( G' ( H ( Z )), G'_{Z 0} ) и проверить равенство одного из расстояний нулю и равенство кодовых слов G' ( H ( Z )), принятых на последних двух тактах. На основе двух решений выбирается следующее состояние, причем переход к состоянию «0» говорит о восстановлении достоверного адреса и выводе его в сдвиговый регистр из переменных B ₁ , B ₂ и B ₃ .

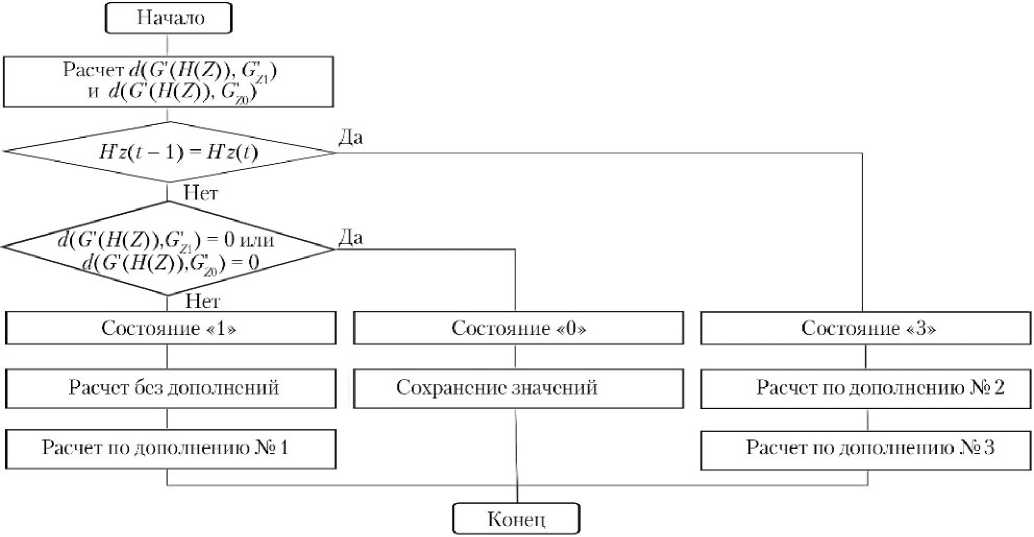
Рис. 7. Блок-схема алгоритма перехода из состояния «0»

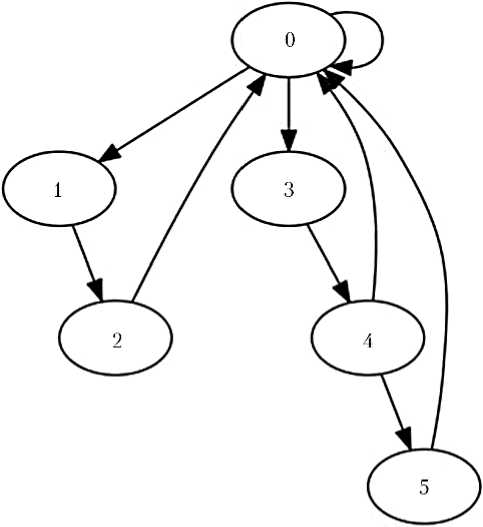
Рис. 6. Граф конечного автомата, описывающего декодирование слов G'Z

Переход к состояниям «1» и «3» говорит о наличии сбоев при формировании адреса. При решении каждой из ветвей: «1» – «2» или «3» – «4» – «5», решается параллельно по два алгоритма на каждом этапе, а окончательное решение выбирается при переходе к состоянию «0».

При переходе из состояния «0» в «1» решаются следующие алгоритмы:

• •    без дополнений — для сбоя кодового слова на этапе передачи. На данном этапе сохраняются оба модифицированных регистра Н_Z' ₁ и Н_Z' _{0 '} , а адрес признается верным;

• •    дополнение № 1 — для сбоя при формировании адреса. Перебираются все возможные варианты адресов и значений, записываемых в регистр, на их основе рассчитываются расстояния Хем-минга между ними и принятым словом. Выбирается слово с нулевым расстоянием, и все его параметры сохраняются для дальнейших расчетов.

При переходе из состояния «0» в «3» решаются следующие алгоритмы:

• •    дополнение № 2 — для сбоев в циклически перезаписываемом регистре. Адрес принимается достоверным, а модифицируемый символ инвертируется, таким образом формируя значение регистра Н_Z' для дальнейших расчетов.

• •    дополнение № 3 — для сбоев при формировании адреса. Для дальнейших расчетов перезаписываются значения, сохраненные на предыдущем такте, без изменений.

На следующем такте для всех трех дополнений обоих переходов («1» – «2» и «3» – «4») производятся модификация регистров Н_Z' ₁ и Н_Z' ₀ , исходя из параметров, сохраненных на предыдущем такте; расчет расстояний d ( G' ( H ( Z )), G'_{Z 1} ) и d ( G' ( H ( Z )), G'_{Z 0} ) и выбор нулевого расстояния; сохранение параметров для следующего перехода и переход к состоянию соответствующего дополнения. Расчет для алгоритма без дополнений отличается необходимостью формировать регистры Н_Z' ₁ и Н_Z' ₀ для каждого из сохраненных на предыдущем такте значений и соответственно выбирать нулевое расстояние из четырех значений вариантов модифицированных кодовых слов.

На третьем такте для состояния «2» осуществляется безусловный переход к состоянию «0». Решение выбирается, исходя из условия равенства кодовых слов G'(H(Z)), принятых на последних двух тактах. В случае истинности условия правильным признается дополнение № 1, для которого производится расчет, аналогичный предыдущему такту, и формируются решения всех трех переменных A1, A2 и A3. При ложности условия производится расчет, аналогичный дополнению № 1, но на основе данных, полученных для решения без дополнений при состоянии «1», решения также выводятся в переменные A1, A2 и A3.

Для состояния «4» сначала проверяется наличие решений по дополнению № 3, аналогично состоянию «3», в случае наличия расстояния Хемминга, равного нулю, формируются решения всех трех переменных A ₁ , A ₂ и A ₃ , и осуществляется переход к состоянию «0». Если решений нет, то производится аналогичный расчет для исходных данных дополнения № 2, а также осуществляется переход к состоянию «5» с параллельным сохранением обоих модифицированных регистров Н_Z' ₁ и Н_Z' ₀ и выводом решений A ₁ и A ₂ , что позволяет не увеличивать задержку до трех тактов. Если решение находится, то производятся операции, аналогичные дополнению № 3 на данном такте.

Переход из состояния «5» в «0» осуществляется на следующем такте параллельно с расчетом оставшегося адреса A ₃ , аналогично решению без дополнений при состоянии «1».

После восстановления адреса восстанавливаются сбои в символах исходного сообщения с помощью алгоритма, идентичного декодированию избыточного символа без дополнений, т. е. с задержкой в один такт.

реализация

Математическая модель разработанного метода радиационно-стойкого кодирования для проведения покрывающего тестирования была реализована в среде Matlab . В основе проверки лежало тестирование потоков управления по принципу «белого ящика» с покрытия пятого уровня [11]. В соответствии с выбранным уровнем проверялись следующие покрытия:

• •    покрытие ответвлений — каждая точка разветвления кода алгоритма проверяется хотя бы один раз;

• •    покрытие условий — условия, имеющие два и более вариантов решения, проверяются при выполнении каждого случая хотя бы по разу;

• •    покрытие ответвлений и условий — суммарные проверки каждого условия и ответвления.

Тестирование показало, что алгоритм метода кодирования позволяет решать со 100%-ной вероятностью следующие задачи:

• •    исправление ошибок в каналах передачи кодовых слов из символов исходного сообщения и избыточного символа;

• •    исправление ошибки, связанной с инверсией значений отдельных битов, хранимых в циклически перезаписываемых регистрах;

• •    коррекция адреса, используемого для декодирования при ошибке в схеме формирования адреса кодера.

Проверенный алгоритм был реализован на языке описания VHDL для интегрирования в кристалл ПЛИС. Для моделирования сбоев был разработан триггер, имеющий дополнительный вход, имитирующий радиационный сбой, и на его основе строилась схема базовой ПЛИС. Схема, представленная на рис. 5, была реализована в макете, в котором в качестве базовой ПЛИС выступала микросхема 5576ХС7Т, а в качестве двух локальных ПЛИС и объектов управления — Actel A3PE1500-PQ208 [12].

Кодер избыточного символа, включая схемы генератора адреса и генератора избыточного символа, занял 56 логических элементов, что составляет 3% от всего объема ПЛИС 5576ХС7Т.

Декодер избыточного символа — 320 логических элементов или 18% объема ПЛИС.

Кодер одного символа исходного сообщения занял 34 логических элемента или 2% объема ПЛИС.

Декодер одного символа избыточного сообщения занял 120 логических элементов или 7% объема ПЛИС.

заключение

В работе предложен новый подход к реализации межкристальной связи ПЛИС, позволяющий за счет радиационно-стойкого кодирования на основе сверточного кода значительно повысить достоверность передаваемой информации и исключить влияние на нее внешних факторов космического пространства.

Данный подход разделяет борьбу с радиационными сбоями на два процесса: исправление ошибок в передаваемых данных и подмена понятия сбоев в генераторе адреса на асинхронное изменение значения адреса для декодера.

Исходя из объемов, занятых реализованным алгоритмом кодирования, можно сделать вывод, что если целью является разгрузка базовой ПЛИС, в частности, для реализации дополнительных алгоритмов защиты, то за счет использования (3%+ k ₀ ·2%) от объема ПЛИС 5576ХС7Т можно перенести часть функций, занимающих значительно больший объем, в локальные ПЛИС. Стоит отметить, что с расширением номенклатуры ПЛИС российского производства и соответствующим повышением количества логических элементов на кристалл применение данного подхода позволит реализовывать более сложные алгоритмы за счет использования защищенных обратных связей из локальных ПЛИС в базовую.

Также важным моментом является то, что суммарная задержка для полного цикла составила не более трех тактов или 1,5 мкс (для частоты 2 МГц), что позволяет использовать данный подход без значительного изменения протоколов внешних взаимодействий прибора.

Так как разработанный метод позволяет абстрагироваться от физической модели радиационного сбоя и исходить только из электрических параметров типа отказа ( SEU, SET или SEL ), то результаты работы можно использовать при разработке бортовых приборов для перспективных КА как на околоземной орбите, так и для межпланетных миссий.