Реализация разностного решения уравнений Максвелла на графических процессорах методом пирамид

Метод разностного решения уравнений Максвелла во временной области (FDTD) [1] широко используется в современных исследованиях при моделировании: распространения излучения [2], материалов с новыми свойствами [3], взаимодействия излучения с биологическими объектами [4] и во многих других приложениях.

Популярность метода обусловлена методической наглядностью (основан на замене производных разностными отношениями), обширностью сферы применения (строгая теория дифракции) и обилием готовых программных реализаций (множество коммерческих и свободно распространяемых пакетов для различных архитектур и операционных систем). Платой за универсальность являются высокие системные требования к быстродействию процессора и объему оперативной памяти, в силу которых разработанный полвека назад метод начал активно применяться в вычислительной практике только сейчас.

Сталкиваясь с известными трудностями («кремниевый тупик»), развитие аппаратной базы вычислительной техники в последнее десятилетие связывается не с наращиванием тактовой частоты процессоров, а со специализированными архитектурными решениями, позволяющими значительно увеличить быстродействие операций определенного типа. Наиболее заметные успехи в этом направлении достигнуты при развитии архитектуры графических процессоров (GPU) и соответствующих программных инструментов (CUDA [5], OpenCL [6]), позволяющих многократно ускорить действия с векторами и матрицами.

Современные реализации FDTD-метода на GPU [7, 8], в основе которых лежит операция вычитания матриц, характеризуются повышением производительности на порядок по сравнению с вычислениями на центральном процессоре. Однако ограниченный объем видеопамяти (2–6 Гб. по сравнению с 4–32 Гб. оперативной памяти) не позволяет в полной мере использовать преимущество GPU в быстродействии.

Снижение влияния упомянутого фактора представляется авторам весьма актуальной задачей. Для ее решения в настоящей работе предлагается развить метод пирамид [9, 10, 11], основанный на уменьшении интенсивности коммуникаций между оперативной и видеопамятью за счёт дублирования арифметических операций (в частности, FDTD-метода).

1.    Разностная схема Yee

Иллюстрируя применение метода пирамид к разностному решению уравнений Максвелла, авторы остановились на классической схеме Yee для трехмерного случая [12], являющейся в настоящее время наиболее популярным инструментом вычислительной электродинамики [1] и наноплазмоники [13]. Основная особенность этой схемы состоит в раздельном расположении узлов сеточной области для каждой проекции напряженностей электрического и магнитного полей, обеспечивающем повышенный порядок аппроксимации исходной дифференциальной задачи по времени и пространству.

Табл. 1. Коэффициенты сеточных проекций электрического и магнитного полей

A	d	M t	a	I x	b	J y	c	K z
E x			0,5	1
E y					0,5	1
E z							0,5	1
H x	0,5	1			0,5	1	0,5	1
H y	0,5	1	0,5	1			0,5	1
H z	0,5	1	0,5	1	0,5	1

Рассмотрим трехмерную по пространству область вычислительного эксперимента D ³ (0 <  t <  T, 0 <  x <  L_x, 0 < y <  L y , 0 <  z <  L_z ) с наложенной на нее сеточной структурой D_h ³ , в узлах которой {( t m+d , x i+a , y j+b , x k+c ): t m+d =( m + d ) h t , m =0, 1,…,. M–M t , ( M = T/h t ), x i+a =( i+a ) h x , i = 0, 1,…, I–I x , ( I = L x / h x ), y j+b =( j+b ) h y , j = 0, 1,…,J–Jy, (J = Ly/hy), z k+c = ( k+c ) h z , k = 0, 1,…,K–K z , K = L z /h z } определены сеточные проекции поля А " ++ d _{j + b} , k + c .

Значения коэффициентов a, b, c, d для различных сеточных проекций электрического и магнитного полей представлены в табл. 1, пустые ячейки соответствуют нулевому значению коэффициента.

Разностная схема для этой области представлена уравнениями (1)–(6):

H m + 0.5 x i , j + 0.5, к + 0.5

_ D       H m - 0.5

ai , j + 0.5, к + 0.5       x i , j + 0.5, к + 0.5

^^^^^^е

H^m + 0.5 y i + 0.5, j , к + 0.5

_ d н т - 0.5

a i + 0.5, j , к + 0.5      y i + 0.5, j , к + 0.5

^^^^^^е

H m + 0.5 z i + 0.5, j + 0.5, к

_ D_a     н т ^{- 05}

a i + 0.5, j + 0.5, к     zi + 0.5, j + 0.5, к

^^^^^^е

D

D bi+0.5, j, к+0.5

Db i, j+0.5 ,к+0.5

fEm    - zi, j+1, к+0.5 Em zi, j, к+0.5 Em -yi, j+0.5, к+1 Em yi, j+0.5, к ) V        hy hz 7 f Em    - xi+0.5, j, к+1 Em xi+0.5, j, к Em -zi+1, j, к+0.5 Em zi,j ,к+0.5 ) h V           z h x 7 m E-yi+1, j+0.5, к Em yi, j+0.5, к Em -xi+0.5, j+1, к Em xi+0.5, j, к hy h x

,

,

,

V

E m ⁺ 1

x i + 0.5, j , к

C Em ai+0.5, j, к    xi+0.5, j, к

E m ^{+ 1} yi ,j + 0.5, к

_ C Em ai, j +0.5, к    yi, j +0.5, к

E m ^{+ 1}

z i , j , к + 0.5

C Em ai, j, к+0.5     zi, j, к+0.5

+

b i + 0.5, j + 0.5, к

+ C bi, j'+0.5, к

C bi, j', к+0.5

+C bi+0.5, j, к

m + 0.5 H 7 z i + 0.5, j + 0.5, к		- H m + 0.5 z i + 0.5, j - 0.5, к		H m + 0.5 y i + 0.5, j , к + 0.5	-	H m + 0.5 y i + 0.5, j , к - 0.5	)
V		h y			hz		7
f	H m + 0.5 x i , j + 0.5, к + 0.5	-	H m + 0.5 x i , j + 0.5, к - 0.5	H m + 0.5 z i + 0.5, j + 0.5, к	-	H m + 0.5 z i - 0.5, j + 0.5, к	)
V		hz			hx		7
f	H m + 0.5 y i + 0.5, j , к + 0.5	-	H m + 0.5 y i - 0.5, j , к + 0.5	H m + 0.5 x i , j + 0.5, к + 0.5	-	H m + 0.5 x i , j - 0.5, к + 0.5	)
V		hx			h y		7

,

,

,

где

Ca i, ,k

= (1

^^^^^^в

^о i ,j, Л

2 ^е i ,j, к ^£ 0

(1 +

^о i ,j, Л

2 ^е i ,j, к ^£ 0

),

£ 0 , Ц - электрическая и магнитная постоянные, £ j

ц j,j,_k - сеточные относительные электрическая и магнитная проницаемости изотропной линейной бездис-персной среды, о j о* j - сеточные удельные элек-

Cb i, ,k

(1 +

^о i ,j, Л

2 ^£ i ,j, к ^£ 0

),

D a i , , k

^{_ (1 -}

^о * i ,j, Л

2 ^Ц i , j , к ^Ц 0

(1 +

^о * mA

2 ^Ц i , j , к ^Ц 0

),

D bi, ,k

(1 +

^о * и,к ^

2 ^Ц i , j , к ^Ц 0

),

трическая и магнитная проводимости.

При моделировании бесконечного свободного пространства вокруг D ³ наложим на сеточную область поглощающие слои CPML [1] шириной nxPML _1 отсчётов слева и nxPML _2 справа вдоль оси x , nyPML _1 и nyPML _2, nzPML _1 и nzPML _2 по осям y и z соответственно. В табл. 2 представлены диапазоны индексов (в нотации Голуба [13]) для каждой сеточной функции, соответствующие подобластям с наложенными слоями. Выражения (7)–(12) описыва-

ют сеточные уравнения в поглощающих слоях.

Табл. 2. Диапазоны индексов для проекций электрического и магнитного полей

	i						k
E x	–	–		1: nyPML _1		J – nyPML _2+1: J	1: nzPML _1	K – nzPML _2: K
E y	1: nxPML _1	I – nxPML _2+1: I		–		–	1: nzPML _1	K – nzPML _2+1: K
E z	1: nxPML _1	I – nxPML _2+1: I		1: nyPML _1		J – nyPML _2+1: J	–	–
H x	–	–		1: nyPML _1–1		J – nyPML _2+1: J–1	1: nzPML _1–1	K – nzPML _2+1: K –1
H y	1: nxPML _1–1	I – nxPML _2–1: I –1		–		–	1: nzPML _1–1	K – nzPML _2+1: K –1
H z	1: nxPML _1–1	I – nxPML _2+1: I –1		1: nyPML _1–1		J – nyPML _2+1: J –1	–	–
H mm + 0.5    _ D     H m - 0 5   - Db xi , j + 0.5, к + 0.5            a i , j + 0.5, к + 0.5      x i , j + 0.5, к + 0.5           b i , j + 0.5, к + 0.5 H m + 0.5   _ D      H m - 0.5   _ D y i + 0.5, j , к + 0.5            a i + 0.5, j , к + 0.5      y i + 0.5, j , к + 0.5           b i + 0.5, j , к + 0.5 m + 0.5                          m - 0.5					f Em - Em Em - Em z i , j + 1, к + 0.5           z i , j , к + 0.5            yi , j + 0.5, к + 1           yi , j		) + 05 ! . + У m       -y m         ,  (7) H xyi , j + 0.5, к + 0.5             H xzi , j + 0.5, к + 0.5 7 ) — + У m     -У m       , (8) H yzi + 0.5, j , к + 0.5             H xyxi + 0.5, j , к + 0.5 7 ) j + У m     -У m      , (9) H zxi + 0.5, j + 0.5, к             H zyi + 0.5, j + 0.5, к 7 ) 0.5         m + 0.5             m + 0.5
					h         Kz h V             y j + 0.5   y                           z k + 0.5   z f Em - Em Em - Em x i + 0.5, j , к + 1           x i + 0.5, j , к            z i + 1, j , к + 0.5           z i , j
					к h      к h V               z k + 0.5    z                             x i + 0.5    x f Em - Em Em - Em yi + 1, j + 0.5, к           y i , j + 0.5, к            x i + 0.5, j + 1, к           x i + 0
z i + 0.5, j + 0.5, к            a i + 0.5, j + 0.5, к      z i + 0.5, j + 0.5, к E m + 1   _ C   E m   + C x i + 0.5, j , к            a i + 0.5, j , к     x i + 0.5, j , к           b i + 0.5, j , к			b i + 0.5, j + 0.5, к f H m + 0.5 z i + 0.5, j + 0.5		K,   h x i + 0.5    x - H m + 0.5 к            z i + 0.5, j - 0.5, к	K y j + 05 h y Hm + 0.5    _ Hm + 0.5 y i + 0.5, j , к + 0.5            y i + 0.5, j , к -
			V        K y j h y			11                 1               ,            (1 V) К h                             Ex , yi + 0.5, j , к          Ex , zi + 0.5, j , к zk  z                                               7

E

г m +1

y i, j + 0.5, k

_ C  Em  + C ai, j+0.5,k    yi, j+0.5,k          bi, j+0.5,k

m + 0.5

H xi, j+0.5,k+0.5

^^^^^^е

Hm + 0.5 x i , j + 0.5, k - 0.5

^^^^^^^

Hm + 0.5 z i + 0.5, j + 0.5, k

^^^^^^е

H m + 0.5 z i - 0.5, j + 0.5, k

V

к К zk z

к h zi x

+ у ^{m + 0.5}

^E yzi , j' + 0.5, k

^^^^^^^

У ^{m + 0} 5

^Eyx i, j + 0.5, k

,

E

m + 1

z i, j, k + 0.5

_ Ca   Em ai, j, k +0.5     zi, j, k+0.5

+C bi,j,k+0.5

^ H^m + 0.5

y i + 0.5, j , k 0.5

е

Hm + 0.5 y i - 0.5, j , k + 0.5

е

Hm + 0.5 x i , j + 0.5, k + 0.5

е

Hm + 0.5 x i , j - 0.5, k + 0.5

л

V

к h xi x

^K y h

+ у ^{m + 0.5}

^E zxi , j , k + 0.5

е

у ^{m +0}" Ezyi , j , k + 0.5

,

где

У m

H^xy i , j + 0.5, k + 0.5

_ b  у m ^{- 1}

y^{j +} 0.5      H^xy i , j + 0.5, k + 0.5

⁺ c y i + 05

(Em zi

е

E^m z i , j , k + 0.5

ст w , к w , a_w - коэффициенты CFS ( Complex-Frequency-

V

h y

,

Shifted) -тензора. У H _a₽

, У m ^{+ 0.5} для остальных ком- E «P w

у m + 0.5   _ ь у m - 0.5

E xyi + 0.5, j , k         y^j     E xyi + 0.5, j , k

+ c

yj

-I

b = е w

I h t

, c_w

m + 0.5

H 7

z i + 0.5, j + 0.5, k

е

H^m + 0.5 z i + 0.5, j - 0.5, k

Л

V

(

^CT w

CT w ^K w ^{+ K} w a w

h y

-I

e

V

I h

^^^^^^^

,

Л

1 ,

понент определяются аналогично с точностью до замены x , y , z и i , j , k . Коэффициенты b w и c w отличны от 0 только в поглощающих слоях.

По краям сеточной области зададим граничное условие Дирихле, соответствующее идеальному проводнику, когда приведенные в табл. 3 компоненты вектора электрического поля A m + ad _{j + b} , _{k +} c равны 0 на

соответствующих границах при 0 ≤ m ≤ M :

Табл. 3. Граничное условие Дирихле для проекций электрического и магнитного полей

	0 ≤ i ≤ I – I x	0 ≤ j ≤ J – J y	0 ≤ k ≤ K – K z
0 ≤ i ≤ I – I x	-	E m   _ 0, E m    _ 0 x i + 0.5, j ,0                   x i + 0.5, j , K	E m   _ 0, E m   _ 0 x i + 0.5,0, k               xi + 0.5, J , k
0 ≤ j ≤ J – J y	E m    _ 0, E m _ 0 y i , j + 0.5,0                     y i , j + 0.5, K	-	E m    _ 0, E m    _ 0 y 0, j + 0.5, k          ’      yI , j + 0.5, k
0 ≤ k ≤ K – K z	E m   _ 0, E m   _ 0 z i ,0, k + 0.5                   z i , J , k + 0.5	E m   _ 0 , E m    _ 0 z 0, j , k + 0.5                     zI , j , k + 0.5	-

Начальное условие зададим как

E0    _ E0    _ E0    _ 0 , что соответствует от- xi+0.5, j, k           yi, j+0.5, k           zi, j, k+0.5

сутствию излучения в начальный момент времени. Поле вводится в область вычислительного эксперимента с помощью метода результирующего поля [14].

2.    Метод пирамид

Приступая к синтезу алгоритма для организации вычислений по (1–12) на графическом процессоре, остановимся на методе пирамид, позволяющем снять остроту известного ограничения на объем видеопамяти.

Суть классического метода пирамид [10] заключается в следующих предписаниях:

• •    построении пространства итераций циклической конструкции, обеспечивающей вычисления по (1– 12) на всей сеточной области D_h ³ ;

• •    выделении на этом пространстве результирующих итераций, от которых не зависит никакая другая;

• •    отнесении к ведению каждой задачи искомого алгоритма (в терминах модели канал/задача) всех итераций, от которых зависит данная результирующая.

Проблема ограничения памяти графического вычислительного устройства решается в [11] последовательной реализацией таких задач на одной видеокарте, а именно:

• •    пространство итераций разбивается по переменной, отвечающей за шаги по времени, на равные интервалы, к каждому из которых применяется метод пирамид;

• •    необходимо, чтобы все итерации, соответствующие меньшему значению переменной, не зависели от итераций, соответствующих большему значению переменной;

• •    высота пирамид выбирается из соображений минимизации длительности вычислений;

• •    разбиение на задачи может быть одинаковым для всех проходов;

• •    задачи выполняются квазипараллельно, по очереди занимая вычислительное устройство на время, необходимое для выполнения одного прохода;

• •    каждая из задач решается в векторизованном виде.

• 2.1.    Случай одномерной сеточной области

Применение модифицированного подхода к сеточным уравнениям позволяет сократить число коммуникаций, т.к. в нем пересылка данных осуществляется только после расчёта нескольких временных слоёв (их число равно высоте пирамиды), а не на каждом шаге, как в классическом алгоритме. Квази-параллельное исполнение задач позволяет одной задаче монопольно занимать GPU, наиболее полно используя доступную видеопамять.

Особенностью FDTD-метода является выражение каждой сеточной функции через значение сеточных функций на предыдущих временных слоях в явном виде, поэтому метод пирамид применяется ко всем уравнениям (1)–(6) одновременно: на каждом временном шаге рассчитываются все 6 компонент A i ++ d _{j + b} , _{k + c} электромагнитного поля; перед началом расчёта и после завершения обработки пирамиды осуществляется пересылка необходимых значений для всех компонент полей. При этом расчёт полей в поглощающих слоях по формулам (7)–(12) будет производиться только для пирамид, расположенных по краям исходной сеточной области. Количество таких пирамид определяется соотношением ширины поглощающего слоя, ширины основания пирамиды и высоты пирамиды, определяющей ширину области перекрытия.

Проиллюстрируем применение метода пирамид к реализации схемы Yee на GPU на примере одномерной задачи. Для одномерного случая (плоская электромагнитная волна распространяется по направлению Z) от нуля будут отличны только компоненты E x , H y электромагнитного поля и схема Yee сократится до двух уравнений (2), (4), в которых сеточные функции других компонент обнуляются. Расчёт по этим уравнениям требует наличия в оперативной памяти всей сеточной области.

Для обхода этого ограничения в [11] предлагается разбивать сеточную область на подобласти, каждая из которых может быть помещена в память GPU и производить в ней итерации по времени стандартным образом, после чего перемещать обратно на CPU. В случае тривиального алгоритма производится одна итерация по времени, при этом для расчёта r значений E m и H m ^{+ 0.} 5 необходимо x k             y k + 0.5

передать по R = r +2 значений каждой из компонент, так как дифференциальный шаблон затрагивает соседние узлы. Однако этот алгоритм предполагает пересылку данных на каждом временном шаге.

Чтобы этого избежать, в [11] предлагается следующая модификация: для вычисления M слоёв сеточных уравнений (2), (4) необходимо последовательно выполнить s проходов методом пирамид, вычисляя каждый раз n слоёв ( M = sn , n – высота пирамиды). Взаимодействие между задачами происходит через CPU и осуществляется только по окончании прохода, т.е. проходы выполняются независимо каждой из задач. При этом для расчёта в результате прохода r значений E_{x k} и H_{y k} необходимо передать по R = r + 2 n значений каждой из компонент. Число задач ц выбирается исходя из соотношения 2 r ц = 2 K - 1, где K - количество узлов сеточной области по направлению Z .

Множество итераций, выполняемых каждой задачей, представляет собой усеченную пирамиду высотой n , шириной верхнего основания r и нижнего основания R . Это иллюстрирует рис. 1 для второй задачи на примере разбиения области на 3 подзадачи, n =3, r =3, R =9, где квадраты обозначают значения сеточной функции, столбцы – пространственные узлы сетки, строки – временные слои, цифры – номер задачи, вычисляющей значение в данном узле. На каждом временном слое вычисляются значения E и H .

x k           y k + 0.5

Темно-серым обозначены значения, вычисляемые второй задачей, бледно-серым – передаваемые для ее расчёта.

Оценка сверху числа значений сеточной функции, обрабатываемых за один проход одной задачей, для метода пирамид и тривиального алгоритма приведена в табл. 4, при этом для расчёта n временных слоёв тривиальным алгоритмом необходимо выполнить n проходов.

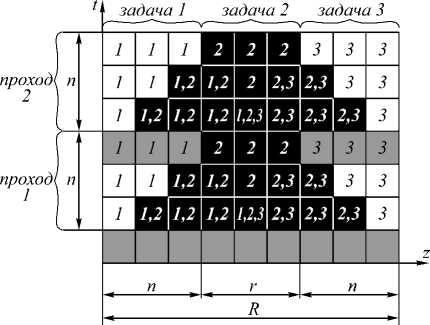
Рис. 1. Декомпозиция сеточной области в одномерном случае для второй задачи

Табл. 4. Оценка числа значений сеточной функции для одной задачи за один проход в одномерном случае

	Тривиальный алгоритм	Метод пирамид
Пересылаемых всего:	4( R –1)	4( R – n )
- в видеопамять	2 R	2 R
- из видеопамяти	2( R –2)	2( R –2 n )
Вычисляемых по шаблону	2( R –2)	2 n ( R – n –1)

Таким образом, для одной задачи число пересылок сокращается в n ( R – 1)/( R – n ) раз, а вычислительная сложность увеличивается в ( R – n –1)/( R –2) раза.

• 2.2.    Случай двумерной сеточной области

Иллюстрируя применение метода пирамид к двумерной сеточной области, рассмотрим пример распространения TM-волны. В этом случае от нуля будут отличны только компоненты E x , H y , H z электромагнитного поля и схема Yee сократится до трёх уравнений (2), (3), (4), в которых сеточные функции других компонент обнуляются.

Тривиальный алгоритм для двумерной по пространству задачи с одномерной декомпозицией сеточной области аналогичен изложенному в п. 2.1. Сеточная область разбивается на равные прямоугольные подобласти размером J × ( R –2), которые могут быть целиком помещены в видеопамять; т.к. для вычисления одного значения требуются значения сеточной функции в соседних узлах. Подобласти должны перекрываться на два сеточных узла по каждой стороне, не прилегающей к краям сеточной области. На каждом шаге по времени производится последовательная обработка подобластей: значения сеточных функций копируются в память GPU, вычисляются значения для следующего временного слоя, вычисленные значения копируются на CPU.

Аналогично для организации вычислений по методу пирамид с одномерной декомпозицией требуется область видеопамяти для размещения по R = r +2 n значений каждой из компонент электромагнитного поля E x , H y , H z для вычисления по r значений для каждой компоненты. Число задач ц выбирается исходя из соотношения 3 r ц = 3 K -1.

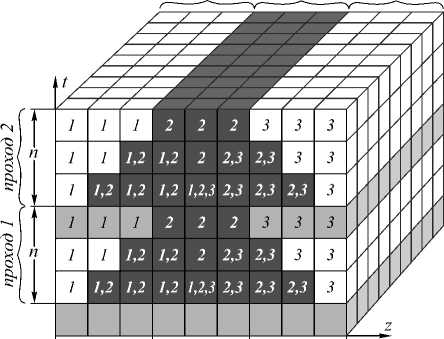
На рис. 2 показана одномерная декомпозиция двумерной области на примере n =3, r =3, R =9, где кубы обозначают значения сеточной функции, столбцы – пространственные узлы сетки, строки – временные слои, цифры – номер задачи, вычисляющей значение в данном узле. На каждом временном слое вычисляются значения E x_j,k , H y_{j,k+ 0,5} , H z_{j +0,5 ,k} .

задача 1 задача 2 задача 3

и            г           и

R

Рис. 2. Декомпозиция сеточной области в одномерном случае для второй задачи

Темно-серым обозначены значения, вычисляемые второй задачей, бледно-серым – получаемые ею от других задач.

Оценка сверху числа значений сеточной функции, обрабатываемых за один проход одной задачей, для метода пирамид и тривиального алгоритма приведена в табл. 5, при этом для расчёта n временных слоёв тривиальным алгоритмом необходимо выполнить n проходов.

Как видно из табл. 5, количество операций отличается от одномерного случая только множителем (3 J –1), соответствующим количеству узлов по направлению y для компонент E x , H y , H z . Таким образом, для одной задачи число пересылок, так же как и в случае одномерной задачи, сокращается в n ( R – 1)/( R – n ) раз, а вычислительная сложность увеличивается в ( R – n –1)/( R –2) раза.

Табл. 5. Оценка числа значений сеточной функции для одной задачи за один проход в двумерном случае

	Тривиальный алгоритм	Метод пирамид
Пересылаемых всего :	2(3 J –1)( R –1)	2(3 J –1)( R – n )
- в видеопамять	(3 J –1) R	(3 J –1) R
- из видеопамяти	(3 J –1)( R –2)	(3 J –1)( R –2 n )
Вычисляемых по шаблону	(3 J –1)( R –2)	(3 J –1) n ( R – n –1)

• 2.3.    Случай трёхмерной сеточной области с одномерной декомпозицией

В случае трёхмерной сеточной области от нуля отличны все компоненты электромагнитного поля и схема Yee представлена уравнениями (1)–(6).

Методики построения тривиального алгоритма и алгоритма метода пирамид, применяемые к трёхмерной сеточной области при одномерной декомпозиции последней, аналогичны рассмотренным выше с той лишь разницей, что сеточные подобласти, которые выделяются задачам, имеют форму параллелепипедов размером I × J ×( R –2), которые могут быть целиком помещены в видеопамять.

Оценка сверху числа значений сеточной функции, обрабатываемых за один проход одной задачей, для метода пирамид и тривиального алгоритма приведена в табл. 3, при этом для расчёта n временных слоёв тривиальным алгоритмом необходимо выполнить n проходов.

Как видно из табл. 6, количество операций отличается от одномерного случая только множителем (6 IJ – 3 I –3 J + 1), соответствующим количеству узлов в плоскости xy для компонент электромагнитного поля.

Табл. 6. Оценка числа значений сеточной функции для одной задачи за один проход в трехмерном случае

	Тривиальный алгоритм	Метод пирамид
Пересылаемых всего ω c	2(6 IJ –3 I –3 J +1) ( R –1)	2(6 IJ –3 I –3 J +1) ( R – n )
- в видеопамять	(6 IJ –3 I –3 J +1) R	(6 IJ –3 I –3 J +1) R
- из видеопамяти	(6 IJ –3 I –3 J +1) ( R –2)	(6 IJ –3 I –3 J +1) ( R –2 n )
Вычисляемых по шаблону ω n	(6 IJ –3 I –3 J +1) ( R –2)	(6 IJ –3 I –3 J +1) n ( R – n–1 )

На рис. 3 представлена блок-схема алгоритма расчёта по методу пирамид, вычисления по которой описаны в следующем параграфе.

3. Экспериментальное исследование метода пирамид

Ниже описаны эксперименты, проведенные с целью выявления ускорения вычислений при применении метода пирамид к FDTD.

Вычислительные эксперименты по определению ускорения проводились на видеокарте NVIDIA GeForce GTX 660 Ti (табл. 7) и процессоре Intel Core 2 Duo E8500 (табл. 8). Исследование велось в операционной системе Ubuntu.

• 3.1.    Программная реализация FDTD-метода

Рассмотрим распространение плоской волны в трехмерной области свободного пространства, ограниченной поглощающими слоями CPML, для чего будем рассматривать уравнения (1)–(6), решение которых соответствует моделированию распространения поля в подобласти без PML; (7)–(12) – в подобласти с PML и (13) – как начальное условие.

Зададим сеточную область размером 256×256×256 отсчётов по пространству, ширину поглощающего слоя выберем nxPML = nyPML = nzPML = 11 отсчётов. Для размещения такой задачи в памяти видеокарты необходимо 467 Мб.

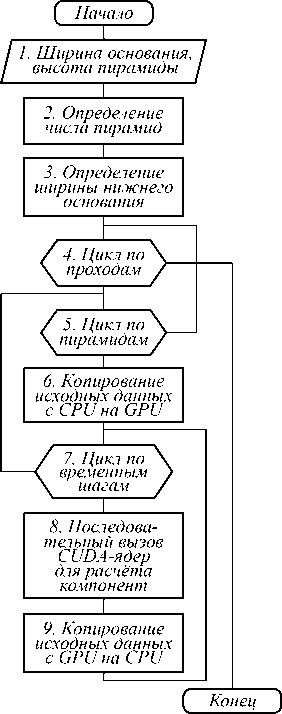
Рис. 3. Схема алгоритма метода пирамид

Табл. 7. Основные характеристики GPU NVIDIA GeForce GTX 660 Ti

Характеристика	Значение
Количество мультипроцессоров, шт.	7
Размер видеопамяти, Гб	2
Максимальное число потоков в блоке, шт.	1024
Максимальная размерность блока потоков ( x , y , z ), шт.	1024×1024×128
Максимальная размерность сетки блоков, шт.	2147483×65535×65535
Тактовая частота ядра, МГц	1032
Тактовая частота памяти, МГц	6008

Табл. 8. Основные характеристики СPU Intel Core 2 Duo E8500

Характеристика	Значение
Тактовая частота ядра, ГГц	3,16
Тактовая частота шины СPU, МГц	1333
Кеш L1, Кб	64×2
Кеш L2, Кб	6144

Применим метод пирамид с одномерной декомпозицией и проведем разбиение исходной сеточной области по направлению K . Ниже приведен исходный код, описывающий алгоритм, приведённый на рис. 3:

__host__ void raschetGPU_pyramid_1d() {

...

//Число запускаемых блоков int SIZEx = ((Imax-1)%BLOCK_DIMx==0) ? (Imax-1)/BLOCK_DIMx : (Imax-1)/BLOCK_DIMx+1;

int SIZEy = ((Jmax-1)%BLOCK_DIMy==0) ? (Jmax-1)/BLOCK_DIMy : (Jmax-1)/BLOCK_DIMy+1;

dim3 gridSize = dim3(SIZEx,SIZEy, 1);

dim3 blockSize = dim3(BLOCK_DIMx,BLOCK_DIMy, BLOCK_DIMz);

create_temp_fields();//Копирование   пересекаю-

//щихся областей во временный буфер int countPyramidsK = ceil((Kmax-1) / (pyramidBaseLengthK + 0.0f));

// Число пирамид (п. 2 на рисунке 3)

int currentTime = 1;//Текущий временной шаг int timeOfPass =((nmax)%PASS==0)? nmax/PASS : nmax/PASS+1;

// Число проходов (п. 3 на рисунке 3)

//Цикл по проходам (п. 4 на рисунке 3)

for (int pass = 1; pass <= PASS; pass++) { int currentBaseLengthK; //ширина по К верх-//него основания текущей пирамиды int leftOffsetK; //ширина левого перекрытия //по К нижнего основания пирамиды int rightOffsetK; //ширина правого перекры-//тия по К нижнего основания пирамиды int fullBaseLengthK; //ширина по К нижнего //основания текущей пирамиды int leftPyramidBorderK; //индекс левой грани-//цы основания пирамиды int rightPyramidBorderK;//индекс правой гра-//ницы основания пирамиды int durationOfTimePass = timeOfPass * pass; //временной шаг, соответствующий окончанию //текущего прохода

//Копируем во временный буфер начальные зна-//чения полей для прохода copyFields(...);

//Цикл по пирамидам (п. 5 на рисунке 3) for(int pyramidIdK =   0; pyramidIdK < countPyramidsK; pyramidIdK++)

&rightOffsetK);

&leftPyramidBorderK, &rightPyramidBorderK);

//Копирование полей на видеокарту (п. 6 на //рисунке 3)

create_arrays_on_GPU(Imax,Jmax,fullBaseLengthK); copy_temp_arrays_to_GPU(0,0,leftPyramidBord erK,Imax,Jmax,fullBaseLengthK);

copy_constant_to_device();

//Цикл по времени внутри прохода

//(п. 7 на рисунке 3)

for (int n = currentTime; n <= durationOfT-imePass & n <=nmax; n++)

{

//(п. 8 на рисунке 3)

//Ядро для пересчёта компонент магнитного //поля на GPU kernelH_pyramid1<<>>(...); cudaEventSynchronize(syncEvent);

//Ядро для пересчёта компонент электриче-//ского поля на GPU kenelE_pyramid1<<>>(...);

cudaEventSynchronize(syncEvent);

}

//Копирование данных из видеопамяти (п. 9 //на рисунке 3)

copy_arrays_from_GPU_with_offset(currentBas eLengthK, startPyramidBasePositionK, left-OffsetK);

delete_arrays_on_GPU();

} currentTime = durationOfTimePass +1;

}

...

}

Сеточные подобласти, соответствующие нижним основаниям пирамид и содержащие начальные данные для каждого прохода, пересекаются (аналогично показанному на рис. 1, 2 для одномерного и двумерного случаев соответственно), поэтому перед началом очередного прохода необходимо скопировать эти области во временный буфер (реализуется процедурой cre-ate_temp_fields()), чтобы значения не были изменены при копировании из видеопамяти значений, рассчитанных при обработке соседней пирамиды.

• 3.2.    Постановка вычислительных экспериментов

Исследуя условия эффективности применения метода пирамид, проведем две серии вычислительных экспериментов, ограничив объем используемой видеопамяти 128 и 256 Мб, что позволит построить до 16 (в первом случае) и 4 (во втором) пирамид с разной шириной основания и высотой. Целью экспериментов будет определение зависимости ускорения вычислений от данных параметров.

На рис. 4 и 5, в табл. 9 и 10 приведены результаты измерений длительности вычислений.

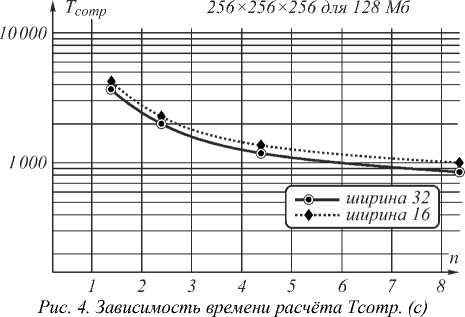
от высоты (число отсчётов) пирамиды для различной ширины основания (128Мб)

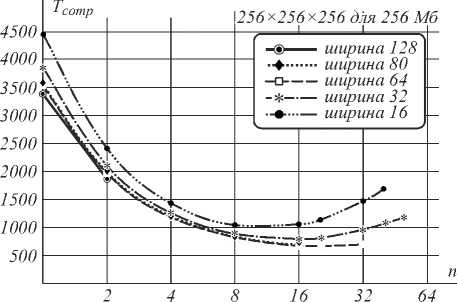
Рис. 5. Зависимость времени расчёта Tcomp. (с) от высоты (число отсчётов) пирамиды для различной ширины основания (256Мб)

Как показали результаты экспериментов, минимальное время вычислений достигается при соблюдении баланса использования памяти устройства и числа пересылок. В эксперименте это достигнуто при использовании пирамид с шириной основания 32 и высотой 8 отсчётов при использовании 128 Мб памяти; пирамид с шириной основания 64 и высотой 20 отсчётов при использовании 256 Мб памяти.

Табл. 9. Зависимость времени расчёта (с) от высоты (число отсчётов) пирамиды для различной ширины основания

µ	r	n	Объём памяти для расчёта одной пирамиды, Мб	Время расчёта, с	Ускорение
8	32	1	81	3854	1
8	32	2	84	2091	1,84
8	32	4	91	1253	3,07
8	32	8	105	879	4,38
16	16	1	53	4456	0,86
16	16	2	56	2400	1,61
16	16	4	63	1436	2,68
16	16	8	77	1035	3,72

Табл. 10. Зависимость времени расчёта (с) от высоты (число отсчётов) пирамиды для различной ширины основания

µ	r	n	Объем памяти для расчёта одной пирамиды, Мб	Время расчёта, с	Ускорение
2	128	1	246	3403	1
2	128	2	248	1896	1,79
4	80	1	164	3560	0,96
4	80	2	168	1969	1,73
4	80	4	175	1190	2,86
4	80	8	189	820	4,15
4	80	16	216	683	4,98
4	64	1	136	3561	0,96
4	64	2	140	1960	1,74
4	64	4	147	1184	2,87
4	64	8	161	814	4,18
4	64	16	189	673	5,05
4	64	20	202	660	5,16
4	64	32	244	694	4,90
8	32	1	81	3855	0,88
8	32	2	84	2092	1,63
8	32	4	91	1254	2,71
8	32	8	105	880	3,86
8	32	16	133	795	4,28
8	32	20	147	809	4,21
8	32	32	189	956	3,55
8	32	40	216	1062	3,20
8	32	50	251	1177	2,89
16	16	1	53	4457	0,76
16	16	2	56	2400	1,41
16	16	4	63	1436	2,37
16	16	8	77	1035	3,29
16	16	16	105	1054	3,23
16	16	20	119	1121	3,03
16	16	32	161	1464	2,32
16	16	40	189	1682	2,02

При дальнейшем увеличении высоты пирамиды время расчёта начинает увеличиваться за счёт увеличения объема дублирующихся данных, что иллюстрируется U-образной зависимостью времени вычислений от высоты пирамиды. На рис. 4 зависимость имеет линейный характер, однако ограничение памяти в 128 Мб не позволяет более увеличивать высоту пирамиды при указанной ширине основания, в результате чего невозможно достигнуть превышения объема дублирующихся вычислений над временем пересылки, что хорошо видно при ограничении памяти в 256 Мб.

Заключение

Представленная реализация FDTD с использованием метода пирамид позволяет снизить влияние ограниченного объема памяти графического процессора и использовать преимущество GPU в быстродействии за счёт снижения интенсивности коммуникаций между оперативной и видеопамятью за счёт дублирования арифметических операций.

При реализации вычислений по методу пирамид важно соблюдать баланс между объемом пересылок и задействованным объемом памяти: определяя ширину основания пирамиды при фиксированной высоте, необходимо выбирать максимально допустимую ширину основания, так как это сокращает число пересылок. Расчёты, произведенные с использованием пирамид одинаковой высоты, имеют близкие значения ускорения, что также подчеркивает значительность затрат на пересылку данных по сравнению с затратами на непосредственный расчёт.

Работа выполнена при поддержке гранта РФФИ 14-07-00291-а.