Реализация рекурсивного цифрового фильтра на основе штрафного p-сплайна
Автор: Кочегурова Елена Алексеевна, У Даньни
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы и анализ данных
Статья в выпуске: 6 т.42, 2018 года.
Бесплатный доступ
В работе показана возможность проектирования рекурсивного цифрового фильтра с использованием штрафного P-сплайна. Аналитически получены и исследованы частотные и временные характеристики сплайн-фильтра для данных, поступающих в режиме реального времени. Исследовано влияние параметров штрафного P-сплайна на показатели эффективности интерпретации входной измерительной информации. Закономерности, полученные в процессе частотного анализа сплайн-фильтра, подтверждены примером восстановления доплеровской функции.
P-сплайн, сглаживающий сплайн, рекурсивный цифровой фильтр, аппаратная функция, системная функция
Короткий адрес: https://sciup.org/140238460
IDR: 140238460 | DOI: 10.18287/2412-6179-2018-42-6-1083-1092
Текст научной статьи Реализация рекурсивного цифрового фильтра на основе штрафного p-сплайна
Эффективность систем обработки информации во многом определяется качеством входной информации, поступающей от реальных объектов наблюдения и управления. Поэтому в составе современных вычислительных устройств нередко присутствуют цифровые фильтры (ЦФ), реализованные аппаратно или программно. При аппаратной реализации системная (аппаратная) функция измерительного преобразователя корректируется динамическим звеном с заданной передаточной функцией [1]. Алгоритмическое или программное сглаживание основано на использовании математических методов цифровой фильтрации. Основными методами цифровой фильтрации для данной задачи являются частотная селекция сигналов и оптимальная (адаптивная) фильтрация [2, 3].
Требования к характеристикам современных ЦФ весьма высоки и определяются селективными свойствами фильтров [4–7]. Так, во временной области эти требования определяются точностью и сохранением формы полезного сигнала. В частотной – требованиями к полосе пропускания сигнала и подавлению помехи. Стремление к сокращению переходной зоны между этими полосами приводит к увеличению окна и, соответственно, порядка фильтра [8].
Альтернативное решение основано на применении рекурсивных фильтров, имеющих бесконечную импульсную характеристику (БИХ-фильтр) при невысоком порядке ЦФ.
Классические методы создания БИХ-фильтров базируются на их аналоговом прототипе с последующей аппроксимацией требуемых свойств фильтра на основе физически реализуемой дискретной системы [2, 3, 9]. При таком подходе требования к ЦФ полностью определены требованиями к АЧХ (реже к ФЧХ) фильтра. Это снижает эффективность фильтрации с позиции последующей интерпретации измерительной информации. Подход к проектированию ЦФ, позволяющий объединить разнообразные требования к качеству фильтрации, возможен на основе численных методов математического программирования.
В задачах интерпретации данных целесообразно использовать модельные функции на основе простого математического базиса. Именно этим объясняется популярность и эффективность сплайн-функций в прикладных задачах интерпретации (прогноз, фильтрация, дифференцирование, выделение тренда и др.) [10–12].
Для создания рекурсивного сплайн-фильтра необходима сплайн-функция, допускающая реализацию в реальном времени, т.е. с рекуррентной формой вычисления. Базисные B -сплайны [13– 17] и штрафные P -сплайны [18–25] имеют высокое быстродействие только при оптимальном выборе узлов. Выбор узлов является одним из способов адаптации сглаживающего сплайна [18, 19, 24–26]. Адаптация значительно повышает эффективность сплайнов.
Другое направление адаптации связано с оценкой штрафного параметра на основе регрессионных и вероятностных подходов [18, 19, 21, 27–29].
Предлагаемая здесь модификация P -сплайна реализует вариационный подход для объединенных в группы данных [30–32]. Создание группы для входных данных автоматически решает проблему выбора узлов. А компактная форма оценки параметров рекуррентной сплайн-функции позволяет реализовать сплайн в реальном масштабе времени (РМВ). Кроме того, анализ частотных и временных характеристик сплайна с позиций ЦФ позволяет более наглядно оценить прикладные свойства сплайна для задач интерпретации данных.
Штрафной P-сплайн для группируемых данных
Получение классического штрафного сплайна S ( t ) по отсчетам y ( t i ), i = 1, n основано на оптимизации специального вида функционала, определенного на всем интервале наблюдения [ a , b ] (B.W. Silverman, 1994)
b
n
n
J ( S ) = X - J [ S Ч t )] 2 d t + £ [ S ( t , ) - y ( t , )] 2 ,
a
i =0
где первое слагаемое вместе со сглаживающим параметром определяет штраф кривизны; второе слагае- мое реализует обычный метод наименьших квадратов.
Для реализации режима реального времени функционал (1) модифицирован [23] и определен для каждого i-го звена сплайна на основании входных данных, собранных в группы по h измерений между отсчетами t0, t‘h с шагом дискретизации At thi
J ( S ) = (1 - р )( h A t ) 2 J [ S"(t )] 2 d t +
1 0 (2)
+ р £ [ S ( t ij ) - y ( t j )] 2 .
j =0
В (2) введен сглаживающий сомножитель р , нормированный по аналогии с [13], но только для каждого звена сплайна. Это сужает диапазон выбора ре [0,1] и придает сглаживающему параметру физический смысл.
Для реализации штрафного сплайна для i -го звена в реальном времени
S i ( т ) = a 0 + a [ -T + ah -т 2 + a 3 -г 3 , - q <т< h - q , (3) нами были получены [32] коэффициенты кубического сплайна в рекуррентном виде. При этом q - номер отсчета t j внутри I -го звена ( j = 0, h ; q = 0, h - 1), в котором сопряжены непрерывные производные сплайна S ( k ) ( t q -+1 ) + = S ( k ) ( t q ) _ , к =0,1 для дефекта 2 и к =0 для дефекта 1. Разрывные коэффициенты ah , a 3 найдены из условия минимизации функционала (2):
d j ( s ) д j ( s )
------= 0,------ = 0 .
д a ‘г д a 3
Соотношение моментов вычисления ( т ) и сопряжения ( q ) i -го звена сплайна порождает несколько вычислительных схем рекуррентного сплайна, подробно исследованных в [33].
Описание штрафного сплайна в виде разностного уравнения
Для исследования рекуррентного сплайна методами теории цифровой фильтрации требуется представить его в виде разностного уравнения. Входной информацией такого фильтра является последовательность измерений I -го звена { y ( t j )}, j = 0, h (решетчатая функция). Выходная инфо рмация - значение сплайна S ( t T ), т = q + 1, q = 0, h - 1. S ( t T ), q = 1, т = 1, h .
Обозначив S i = S ( t T ), получим
S , .-T = S ( t T ) = a 0 , S ' -T = S ' ( t T ) = a [ .
h
Суммы измерений 2 y ( tl k ), входящие в функцио- k =0
нал (2), обозначены для рекуррентного случая как i + h
2 Ук-г. Решетчатые функции {Si}, {y} i = 1,2,3... к=i имеют одинаковый интервал дискретизации, совпадающий с интервалом дискретизации входных данных At.
Для введенных обозначений перепишем уравнение сплайна (3) как разностное уравнение для решетчатой функции { S i }, i = 1,2,3...
Y
0
S
i
-Y
i
где
-
Y 0 = BC - A 2 ;
-
Y 1 ( т ) = Y " + рт 2 ( AH 3 - CH 2) + рт 3 ( AH 2 - BH 3);
-
Y 2( т ) = Y 0 т + рт 2 ( AH 4 - CH 3) + рт 3 ( AH 3 - BH 4);
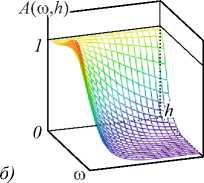
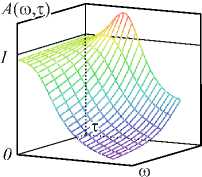
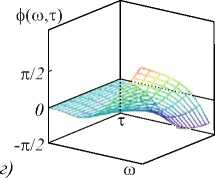
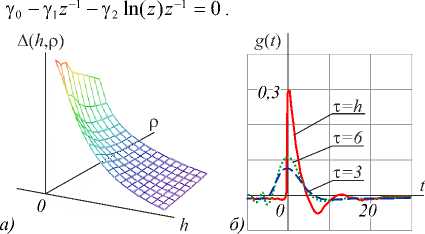
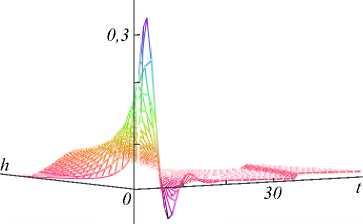
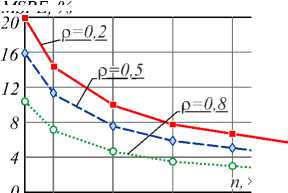
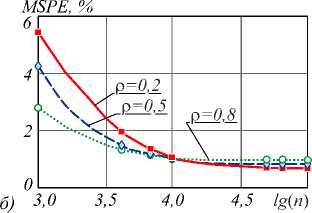
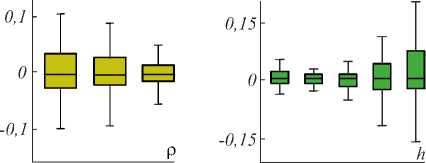
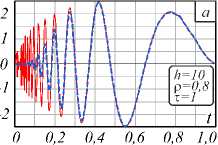
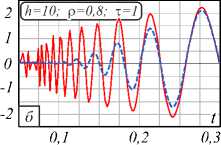
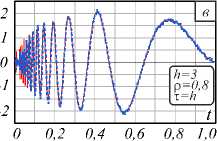
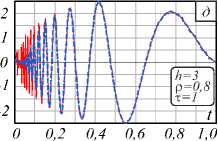
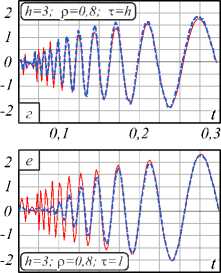
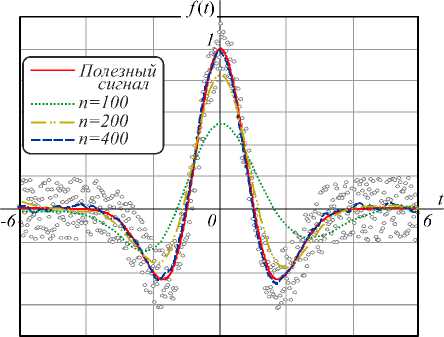
Y3 Y 4 A = 6(1 - р) h4+ р H5; B = 4(1 - р) h3+ р H4; C = 12(1 -р) h5+р H6; h Hn = 2 kn. к=0 Разностное уравнение (4) соответствует уравнению с переменными коэффициентами yj (т), j = 0,4. Порядок уравнения соответствует значению т, те[1, h], где т - момент вычисления значения сплайна. Однако если момент вычисления сплайна т не изменяется на разных звеньях, то коэффициенты Yj, j = 0,4, будут постоянными относительно звена сплайна и параметр т опускается. В (4) и далее q = 0, т.е. сопряжение звеньев сплайна осуществляется в начале звена. Последовательно раскладывая в выражении (4) Si-т,Si-T и далее Si-^,S,'_2t,...,S0,S0 (что соответствует разложению непрерывных коэффициентов сплайна a0-1, a/-1, a0-2, a/-2,...,a00, a"), получаем разностное уравнение в виде h si =2 l=0 i+h Qi (р, h, q)2 yk-т (к -т)2 + к=i i+h +Q2<р, h, q )2 yk-т (к -т)3 к=i + C . Вид разностного уравнения (5) указывает на линейность уравнения относительно измерений y(tk). Причем коэффициенты Ql (р, h, q), Q2 (р, h, q) полностью определены настроечными параметрами сплайна р, h, q, а константа C зависит только от начальных условий сплайна. Для подтверждения линейности сплайн-фильтра проведены эксперименты по оценке свойств линейных преобразований: сохранение частотного состава входного гармонического сигнала и сохранение закона распределения плотности вероятности входного случайного сигнала [2, 3]. Было установлено, что в спектре выходного сигнала после сплайн- преобразования не появляются дополнительные значимые гармоники. Их амплитуда составляет (0,00001-3)% от амплитуд существующих гармоник во входном сигнале. Также установлено, что после сплайн-преобразования случайного сигнала типа белый шум в ограниченной полосе частот с нормальным законом распределения выходной сигнал также подчинен нормальному закону распределения. Согласованность эмпирического закона распределения с теоретическим, рассчитанная по х2— критерию Пирсона, составляет 96% (при объеме выборки 1000 значений). Линейность сплайн-фильтра делает возможным использовать для его исследования аппарат линейных динамических систем. Исследование частотных и временных характеристик рекурсивного сплайн-фильтра Традиционно проектирование программного ЦФ [5, 8-12] включает задание требуемой передаточной функции фильтра в спектральной области, ее аппроксимацию с заданной точностью, переход в z-область и, наконец, получение импульсной весовой функции на основании обратного z-преобразования. И таким образом, основным математическим инструментом цифровой фильтрации является уравнение свертки аппаратной функции фильтра и входного сигнала [34]. При анализе сплайн-фильтра уравнением преобразования во временной области является уравнение сплайна вида (3) или разностное уравнение (4). Особый интерес для понимания сути и наглядности сплайн-фильтра имеет его описание в частотной области [16, 33, 35-38]. Кроме этого, появляется альтернативное описание сплайн-фильтра во временной и частотной области. Цифровые фильтры по аналогии с линейными динамическими системами могут быть представлены следующими основными характеристиками [4-8]: - системная функция (частотная передаточная или комплексный коэффициент передачи для непрерывных систем); - аппаратная функция (импульсная весовая для непрерывных систем). Для решения разностного уравнения (4) использовано дискретное преобразование Лапласа, в данном случае в форме z-преобразования. Получив изображения левой и правой части уравнения (4) S(z) = Si и Y(z) = y(tТ), можно найти передаточную функцию W(z) = S(z) / Y(z) сплайн-фильтра. Для практического использования целесообразно перейти от системной функции фильтра к комплексному частотному коэффициенту передачи H(ю) = W(еюА*), полагая z = еюи At =1, используя свойства сдвинутых решетчатых функций h £ e(k:'' • ((k - т)2Y3 + (k - т)3Y4) H (ю) = k=0------------------------------. (6) Y0 - Yie ют -Y2®e ют Числитель частотной характеристики определен нерекурсивной частью сплайн-фильтра, знаменатель - рекурсивной. Периодичность функции еюАt приводит к периодичности частотной характеристики H(ю) [2, 3, 8]. Поэтому численное исследование амплитудных и фазовых частотных характеристик сплайн-фильтра проведено в области главных частот [-п / At, п / At], где частотные характеристики дискретного и непрерывного фильтра совпадают, а также исключается эффект алиасинга. Представим частотную характеристику H(ю) в виде H (ю) = A (ю) • e j (ю), где A(ю) = | W(ю)| - амплитудно-частотная характеристика (АЧХ), ф(ю) = агд[ W(ю)] - фазо-частотная характеристика (ФЧХ) фильтра. Основные параметры сплайна значительно изменяют фильтрующие свойства сплайна. Общую картину этих свойств представляют АЧХ и ФЧХ сплайн-фильтра, приведенные на рис. 1. При исследовании параметры сплайна варьировались в диапазоне их определения: сглаживающий множитель ре[0,1], момент вычисления те[1, h], длина звена hе[3,20] (h = 3 соответствует использованию 4 измерений для построения полинома третьего порядка, а при h >20 сплайн сложно использовать в системах реального времени). Вид всех АЧХ на рис. 1 а соответствует низкочастотному фильтру с разной степенью влияния параметров. Если рассматривать сплайн-фильтр как динамическое звено второго порядка, то его коэффициент передачи (1M)J|h (ю)|2аю растет с увеличением параметров т и р. Однако резонансные пики АЧХ возникают при небольших значениях р или h и при приближении т^h. а) в) Рис. 1. АЧХ и ФЧХ рекуррентного фильтра (P-сплайн): а) h = 10, τ = 1, ρ∈[0, 1]; б) h = 10, ρ = 1, h∈[3, 20]; в) h = 10, ρ = 0,5, τ∈[1, h] г) h = 10, ρ = 0,5, τ∈[1, h] На характер ФЧХ (рис. 1г) наибольшее влияние оказывает момент вычисления сплайна т, соответствует ФЧХ системы с запаздыванием. В данной реализации сплайн-фильтра имеем дело с обработкой информации группами [32]. В силу этого ФЧХ имеет опережающий характер, и лишь при т^h появляется отставание фазовой характеристики. На полосу пропускания сигнала не столь существенно влияют параметры сплайна т и р, как длина звена сплайна h. И это очевидно, так как при увеличении h сплайн становится более гладким и полоса пропускания уменьшается. Это свойство сплайн-фильтра подтверждено ниже на рис. 2а при анализе ширины аппаратной функции. При малых значениях h инерционность сплайна снижается и в большей степени соответствует АЧХ интерполяционного сплайна. Для идеального фильтра A(ю) = 1, ф(ю) = 0 в заданной полосе частот. Аналогом импульсной весовой функции линейных динамических систем для дискретных фильтров является аппаратная функция (АФ) g(t) 1 Г g (t) = H (ю) eJ m* dm. 2n < Аппаратная функция часто применяется в уравнении дискретной свертки для аналитической связи сигналов на входе и выходе дискретного фильтра. Для предлагаемого сплайн-фильтра АФ получена аналитически на основе g(t) и системной функции (6). На рис. 2 продемонстрированы семейства АФ при изменении параметров р, h или т. Во всем диапазоне изменения параметров сплайна АФ имеет затухающий характер. Хорошо прослеживается связь между шириной АФ (А(р, h)) и частотными характеристиками сплайн-фильтра: полоса пропускания сигнала обратно пропорциональна ширине АФ. Как и при анализе частотных характеристик, ширина АФ в большей степени зависит от длины звена сплайна h и мало зависит от сглаживающего параметра р (рис. 2а). Более гладкий сигнал на выходе фильтра соответствует использованию большого значения h, т.е. узкой полосе пропускания рис. 1б и большой ширине АФ рис. 2а, б. Момент вычисления т определяет свойство причинности сплайн-фильтра рис. 2в. В данном случае h(t) = 0, t<0 только для значения т = h, т.е. когда нет запаздывания в вычислениях. В остальных случаях h(t) = 0 при т < h - т, что соответствует обработке данных группами или в системах с накопленными данными. Кроме требований к установившимся процессам, эффективность и работоспособность ЦФ характеризуется показателями в переходных процессах и условиями устойчивости. Устойчивость рекурсивного сплайн-фильтра как линейной дискретной системы была оценена аналитически на основе характеристического уравнения [2, 8], соответствующего знаменателю уравнения (6) для т =1 g№ Рис. 2. Аппаратная функция рекуррентного фильтра (P-сплайн): а) he[3, 20], ре[0, 1]; б) т= 1, р= 0,6; в) h = 10, р = 0,6 Преобразуем данное уравнение, умножая его на z и используя разложение ln(z) в степенной ряд, ограничиваясь одним членом разложения: ~ z-1 Y0z-Yi -Y 2 z ■ 2---; = 0. z +1 Или c0 z2 + c1 z + c 2 = 0 . Далее, используя билинейное w-преобразование (Мизеса) z = (1+ m) / (1 - ю), получим u 0 w2 + u1 w + u 2 = 0 , где c0 =Y0; u0 = c0 -C1 + c2; C1 =Y0-Y1 -2Y2; U1 = 2c0 -2c2; c 2 = 2y 2-Y0; u 2 = c0 + c + c 2. Замена переменной z позволяет свести условия устойчивости |z| < 1 к критерию Гурвица и для уравнения второго порядка имеют вид [c0- c1+ c2> 0; < 2c0- 2c2> 0; [ c0+ c1+ c2> 0. А с учетом введенных в (4) обозначений для t = 1 условия устойчивости сплайн-фильтра pY0 + р^ P2 > 0; L^ (P1 - 2P2) > 0; (7) l-р^ P1 > 0, где JP1 = A(H2 + H3) - CH2 -BH3; [ P2 = A (H3 + H4) - CH3 - BH4. Система неравенств (7) определяет условия устойчивости фильтра. Разрешая (7) относительно сглаживающего параметра p, были найдены области устойчивости сплайн-фильтра (табл. 1) при изменении параметров q и h. Табл. 1. Области устойчивости сплайн-фильтра Основная особенность состоит в сужении области устойчивости от момента сопряжения звеньев сплайна q. И при стремлении q к правому концу звена сплайна наблюдается неустойчивость при любом значении параметра р. При сопряжении в начале звена сплайн всегда устойчив и при т < 1. В практических приложениях чаще всего и используется сопряжение в начале звена. Аналитически оценить устойчивость сплайн-фильтра при т >1 затруднительно. Однако косвенно устойчивость преобразования можно оценить на основе зависимости погрешностей а восстановления некоторого модельного сигнала при значительном изменении его длины. Так, на рис. 3а, б представлена зависимость MSPE (Mean Squared Percentage Error) [33] для функции Доплера (8) при изменении числа отсчетов сигнала nе [102,105]. Аддитивный шум N;(0,0,22), т.е. 20% от максимального значения полезного сигнала. MSPE, % х102 а) Рис. 3. Зависимость погрешности восстановления функции от числа отсчетов сигнала, h = 10, р = 0, т = h Изменение погрешности наиболее различимо при изменении сглаживающего множителя р. И на рис. 3 приведено для максимального значения т = h. Качество сплайн-преобразования как программного ЦФ невысокого порядка было оценено прямыми методами по реакции на единичное ступенчатое возмущение. Проведенные исследования показали, что графики переходного процесса (ПП) Н(nТ) имеют колебательный характер. Все показатели ПП: длительность, перерегулирование, колебательность – ухудшаются при т^ h, т.е. при уменьшении запаздывания вычисления сплайна h - т. Для рекуррентного ЦФ важнейшей характеристикой является длительность ПП, которая увеличивается с ростом длины звена сплайна h. И в области изменения параметров сплайна длительность ПП составляет (15-20)Аt, что вполне допустимо в системах реального времени. Результаты вычислительного эксперимента Для оценки исследованного P-сплайна реального времени был выбран часто используемый в сравнительном анализе пример доплеровской функции [18, 19] ( 2п(1 + 0,05)) f(t) =5 vt(t- 1) ■ sin , (8) ( t + 0,05 J заданной на интервале [0, 1] n дискретными отсчетами с аддитивной помехой £(t), N;(0,0,22), т.е. У(ti )=f(ti) + ^( t). Данная функция довольно сложна для математической обработки, имеет значительное изменение частоты, амплитуды и является моделью многих процессов в медицине, оптике и других приложениях, основанных на эффекте Доплера (изменение частоты волн в зависимости от движения источника этих волн относительно наблюдателя). Гистограммы остатков текущего восстановления доплеровской функции в условиях помех N;(0,0,22) приведены на рис. 4 при изменении параметров сплайна р, h. а) б) Рис. 4. Гистограммы остатков текущего восстановления функции (8): а) h = 10, б) ρ = 0,5 Характер и величины остатков подтверждают влияние параметров сплайна на результирующую погрешность, выявленное при частотном анализе сплайн-фильтра. Так, систематическая погрешность, обусловленная шириной аппаратной функции (рис. 2а), растет с увеличением длины звена h или с повышением гладкости сплайна, т.е. с уменьшением р. Ниже на рис. 5 приведены примеры восстановления доплеровской функции предлагаемым P-сплайном в режиме реального времени при изменении параметров сплайна р, h. Исходная функция, так же, как на рис. 4 f [19], задана на интервале [0, 1] в 400 дискретных отсчетах. На рис. 5б, г, е представлены зуммированные части функции, соответствующие высокочастотным фрагментам входного сигнала в начале интервала обработки. Рис. 5. Восстановление P-сплайном в режиме реального времени (серая пунктирная линия). Доплеровская функция (чёрная сплошная линия) 0,1 0,2 0.3 Сопоставляя результаты исследования предлагаемого P-сплайна и приведенные в [18, 19], можно увидеть аналогичное качество восстановления с лучшим из приведенных на рис. 4f в [19] adaptive P-spline. Следует отметить, что adaptive P-spline в [19] использован с учетом адаптации сглаживающего параметра. Визуально качество восстановления доплеровской функции на рис. 4f в [19] соответствует варианту, представленному на рис. 5д, е. Гораздо лучшее восстановление высокочастотного фрагмента входного сигнала продемонстрировано на рис. 4г. В этом и состоит преимущество предлагаемого P-сплайна: доступность изменения параметров сплайна на разных звеньях. Кроме того, P-сплайн допускает реализацию в реальном времени, что является явным достоинством в прикладных задачах интерпретации данных. В качестве другого модельного примера, графически и численно иллюстрирующего свойства рекуррентного сплайн-фильтра, была выбрана функция V(t) = (1 - t2) ■ exp (-^^^ . (9) В вейвлет-анализе данная функция (рис. 6, красная линия) носит название «мексиканская шляпа» и используется в качестве материнского вейвлета в задачах, требующих хорошего пространственного раз- решения и не требовательных к спектральному разрешению. Рис. 6. Восстановление P-сплайном в режиме реального времени функции «мексиканская шляпа» при изменении числа отсчетов функции n, h = 10, р = 0,5 На интервале [–10, 10] функция (9) задана n отсчетами. Аддитивная смесь сигнала и помехи £(t) показаны на рис. 6 точками для n = 500. Следует отметить, что число отсчетов n является самым влиятельным параметром восстановления данной функции (9). И, как видно из рис. 6, удовлетворительное качество фильтрации в РМВ возможно для n =400 (серая пунктирная линия, графически совпадающая с полезным сигналом). Погрешность MSPE (%) для этого случая составляет 1,29% при с = 0,2 (20% от максимального значения полезного сигнала). Для других значений параметров погрешности приведены в табл. 2 для h = 10 и ρ = 0,5. Табл. 2. Погрешности MSPE n 1 С 0 5 10 15 20 100 11,9 11,97 12,0 12,12 12,6 200 4,06 4,07 4,11 4,29 4,31 400 0,85 0,87 1,01 1,19 1,29 500 0,5 0,57 0,78 0,89 1,05 1000 0,1 0,28 0,5 0,86 1,1 При нулевой погрешности удовлетворительные данные достигнуты при n > 400, и в диапазоне n е 4■Ю3-105 погрешность составляет 10 2- 10 5. Анализ доплеровской функции позволил графически иллюстрировать исследованные частотные свойства P-сплайна реального времени. При уменьшении длины сплайна h увеличивается его пропускная способность (рис. 1б), что особенно хорошо проявляется при восстановлении высокочастотных сигналов (рис. 4г, е). Однако при увеличении момента вычисления т (рис. 4в) появляются нежелательные осцилляции (всплески) восстановленной функции, обусловленные появлением пиков АЧХ, рис. 1 в при т^h. Именно в возможности варьировать параметры сплайна на разных звеньях в зависимости от изменения свойств поступающей информации состоит потенциал P-сплайна реального времени. Заключение В работе показана возможность представления рекуррентного P-сплайна в виде цифрового фильтра с бесконечной импульсной характеристикой и переменными параметрами. Аналитически найденная системная функция фильтра позволила исследовать частотные характеристики сплайн-фильтра и установить, что во всем диапазоне параметров сплайна фильтр остается низкочастотным. Селективные свойства сплайн-фильтра наиболее ясно иллюстрируются шириной аппаратной функции, которая значительно зависит от параметров сплайна. Исследование влияния основных параметров P-сплайна показало, что на полосу пропускания в большей степени влияет число отсчетов в звене сплайна h (число нерекурсивных членов разностного уравнения). Закономерности, установленные при частотном анализе сплайн-фильтра, подтверждены восстановлением в реальном времени доплеровской функции. Работа выполнена при поддержке гранта РФФИ (№ 18-07-01007).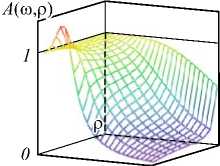
h/q
0
1
2
3
4
5
6
7
3
0–1
0–0,99
0,99–1
6
0–1
0–1
0–0,98
0,90–1
0,99 – 1
8
0–1
0–1
0–1
0–0,97
0,87 – 1
0,97– 1
н
н
10
0–1
0–1
0–1
0–0,99
0– 0,95
0,84– 1
0,95– 1
н
н – неустойчив
Список литературы Реализация рекурсивного цифрового фильтра на основе штрафного p-сплайна
- Ланге, П.К. Коррекция динамической погрешности инерционного измерительного преобразователя/П.К. Ланге//Вестник Самарского государственного технического университета. Серия: Технические науки. -2017. -№ 2(54). -С. 58-64.
- Сергиенко, А.Б. Цифровая обработка сигналов: учебн. пособие для вузов/А.Б. Сергиенко. -4-е изд. -СПб.: БХВ-Петербург, 2011. -758 с. -ISBN: 978-5-9775-0606-9.
- Оппенгейм, А. Цифровая обработка сигналов/А. Оппенгейм, Р. Шафер; пер. с англ. -М.: Техносфера, 2007. -856 с. -ISBN: 978-5-94836-135-2.
- Бугров, В.Н. Синтез целочисленных рекурсивных фильтров с произвольно заданными селективными требованиями/В.Н. Бугров//Цифровая обработка сигналов. -2016. -№ 2. -С. 35-43.
- Manolakis, D. Applied digital signal processing: Theory and practice/D. Manolakis, V. Ingle. -Cambridge: Cambridge University Press, 2011. -1009 p. -ISBN: 978-0-521-11002-0.
- Карпенков, А.С. Методика расчёта целочисленного цифрового селекторного нерекурсивного фильтра c заданными добротностью и уровнем подавления/А.С. Карпенков, Ю.В. Гришанович, Д.С. Потехин, Е.П. Тетерин//Вестник Нижегородского университета им. Н.И. Лобачевского. -2009. -№ 6-1. -С. 79-85.
- Никитин, Д.А. Приложения алгоритма синтеза рекурсивных цифровых фильтров по импульсной характеристике/Д.А. Никитин//Цифровая обработка сигналов. -2009. -№ 4. -С. 8-15.
- Давыдов, А.В. Цифровая обработка сигналов: Тематические лекции/А.В. Давыдов. -Екатеринбург: ИГиГ, ГИН, Фонд электронных документов, 2005. -185 с.
- Турулин, И.И. Методика синтеза управляемых цифровых фильтров на основе аналоговых прототипов/И.И. Турулин, Ю.И. Булгакова//Известия ЮФУ. Технические науки. -2011. -№ 2(115). -С. 88-92.
- Гетманов, В.Г. Методы вычисления аппроксимационных сплайновых функций для задач цифровой фильтрации/В.Г. Гетманов//Известия Российской академии наук. Теория и системы управления. -2016. -№ 5. -С. 47-57. - DOI: 10.7868/S0002338816040077
- Майстренко, А.В. Применение методов цифрового дифференцирования сигналов для определения стационарности процессов/А.В. Майстренко, А.А. Светлаков//Научный вестник Новосибирского государственного технического университета. -2015. -№ 2(59). -С. 7-19. - DOI: 10.17212/1814-1196-2015-2-7-19
- Zjavka, L. Multi-site post-processing of numerical forecasts using a polynomial network substitution for the general differential equation based on operational calculus/L. Zjavka//Applied Soft Computing Journal. -2018. -Vol. 73. -P. 192-202. - DOI: 10.1016/j.asoc.2018.08.040
- de Boor, C. A practical guide to splines/C. de Boor. -New York: Springer-Verlag, 2001. -348 p. -ISBN: 978-0-387-95366-3.
- Redd, A.A. Comment on the orthogonalization of B-spline basis function and their derivatives/A.A. Redd//Statistics and Computing. -2012. -Vol. 22, Issue 1. -P. 251-257. - DOI: 10.1007/s11222-010-9221-0
- Шумилов, Б.М. Алгоритмы с расщеплением вейвлет-преобразования сплайнов первой степени на неравномерных сетках/Б.М. Шумилов//Журнал вычислительной математики и математической физики. -2016. -Т. 56, № 7. -С. 1236-1247. -10.7868/S0044466916070176.
- Berenguer-Vidal, R. Design of B-spline multidimensional deformable models in the frequency domain/R. Berenguer-Vidal, R. Verdú-Monedero, J. Morales-Sánchez//Mathematical and Computer Modelling. -2013. -Vol. 57, Issue 7-8. -P. 1942-1949. - DOI: 10.1016/j.mcm.2012.01.011
- Gálvez, A. Efficient particle swarm optimization approach for data fitting with free knot B-splines/A. Gálvez, A. Iglesias//Computer-Aided Design. -2011. -Vol. 43, Issue 12. -P. 1683-1692. - DOI: 10.1016/j.cad.2011.07.010
- Krivobokova, T. Fast adaptive penalized splines/T. Krivobokova, C.M. Crainiceanu, G. Kauermann//Journal of Computational and Graphical Statistics. -2008. -Vol. 17, Issue 1. -P. 1-20. - DOI: 10.1198/106186008X287328
- Yang, L. Adaptive penalized splines for data smoothing/L. Yang, Y. Hong//Computational Statistics and Data Analysis. -2017. -Vol. 108. -P. 70-83. - DOI: 10.1016/j.csda.2016.10.022
- Kouibia, A. Approximation by discrete variational splines/A. Kouibia, M. Pasadas//Journal of Computational and Applied Mathematics. -2000. -Vol. 116, Issue 1. -P. 145-156. - DOI: 10.1016/S0377-0427(99)00316-7
- Tharmaratnam, K. S-estimation for penalized regression splines/K. Tharmaratnam, G. Claeskens, C. Croux, M. Salibián-Barrera//Journal of Computational and Graphical Statistics. -2010. -Vol. 19, Issue 3. -P. 609-625. - DOI: 10.1198/jcgs.2010.08149
- Cao, J. Estimating curves and derivatives with parametric penalized spline smoothing/J. Cao, J. Cai, L. Wang//Statistics and Computing. -2012. -Vol. 22, Issue 5. -P. 1059-1067. - DOI: 10.1007/s11222-011-9278-4
- Kochegurova, E.A. Real-time recovery of functions and their derivatives by variation splines/E.A. Kochegurova, E.S. Gorokhova//Key Engineering Materials. -2016. -Vol. 685. -P. 920-924. - DOI: 10.4028/www.scientific.net/KEM.685.920
- Eilers, P.H.C. Splines, knots, and penalties/P.H.C. Eilers, B.D. Marx//WIREs Computational Statistics. -2010. -Vol. 2, Issue 6. -P. 637-653. - DOI: 10.1002/wics.125
- Гетманов, В.Г. Алгоритмы вычисления аппроксимационных сплайновых функций с учётом оптимизации расположения сплайновых узлов/В.Г. Гетманов//Автометрия. -2013. -Т. 49, № 1. -С. 26-41.
- Денисов, В.И. Исследование алгоритмов выбора оптимальных координат узловых точек в полупараметрических моделях штрафных сплайнов/В.И. Денисов, В.С. Тимофеев, А.В. Фаддеенков//Научный вестник Новосибирского государственного технического университета. -2013. -Т. 51, № 2. -С. 35-44.
- Aydin, D. Optimum smoothing parameter selection for penalized least squares in form of linear mixed effect models/D. Aydin, M. Memmedli//Optimization. -2012. -Vol. 61, Issue 4. -P. 459-476. - DOI: 10.1080/02331934.2011.574698
- Crainiceanu, C.M. Spatially adaptive Bayesian penalized splines with heteroscedastic errors/C.M. Crainiceanu, D. Ruppert, R.J. Carrol, A. Joshi, B. Goodner//Journal of Computational and Graphical Statistics. -2007. -Vol. 16, Issue 2. -P. 265-288. - DOI: 10.1198/106186007X208768
- Walker, C.G. SALSA -a spatially adaptive local smoothing algorithm/C.G. Walker, M.L. MacKenzie, C.R. Donovan, M.J. O'Sullivan//Journal of Statistical Computation and Simulation. -2011. -Vol. 81, Issue 2. -P. 179-191. - DOI: 10.1080/00949650903229041
- Чичерин, И.В. Сплайн-алгоритмы обработки сигналов измерительной информации в системах автоматизации технологических процессов: дис.. канд. техн. наук: 05.13.06/Чичерин Иван Владимирович. -Новокузнецк, 2006. -173 с.
- Хуторцев, В.В. Использование метода сплайн-функций при синтезе цифровых алгоритмов фильтрации с группированием наблюдений/В.В. Хуторцев, О.С. Федоренко//Радиотехника. -2010. -№ 2. -С. 4-8.
- Кочегурова, Е.А. Текущее оценивание производной нестационарного процесса на основе рекуррентного сглаживающего сплайна/Е.А. Кочегурова, Е.С. Горохова//Автометрия. -2016. -Т. 52, № 3. -С. 79-85. - DOI: 10.3103/S8756699016030109
- Кочегурова, Е.А. Частотный анализ рекуррентных вариационных P-сплайнов/Е.А. Кочегурова, А.И. Кочегуров, Н.Е. Рожкова//Автометрия. -2017. -Т. 53, № 6. -С. 67-76. - DOI: 10.15372/AUT20170608
- Мясников, В.В. Сплайны как средство построения эффективных алгоритмов локального линейного преобразования/В.В. Мясников//Компьютерная оптика. -2007. -Т. 31, № 2. -С. 52-68.
- Mihajlovic, Z. Frequency domain analysis of B-spline interpolation/Z. Mihajlovic, A. Goluban, M. Zagar//ISIE '99. Proceedings of the IEEE International Symposium on Industrial Electronics. -1999. -Vol. 1. -P. 193-198. - DOI: 10.1109/ISIE.1999.801783
- Guo, W. Smoothing spline ANOVA for time-dependent spectral analysis/W. Guo, M. Dai, H.C. Ombao, R. Von Sachs//Journal of the American Statistical Association. -2003. -Vol. 98, Issue 463. -P. 643-652. - DOI: 10.1198/016214503000000549
- Raposo-Sánchez, M.Á. Analog and digital filters with α-splines/M.Á. Raposo-Sánchez, J. Sáez-Landete, F. Cruz-Roldán//Digital Signal Processing: A Review Journal -2017. -Vol. 66. -P. 1-9. - DOI: 10.1016/j.dsp.2017.03.003
- Kukushkin, Y.A. Rhythmocardiogram approximation methods for calculation of spectral parameters of cardiac rhythm variability/Y.A. Kukushkin, A.I. Maistrov, A.V. Bogomolov//Biomedical Engineering. -2010. -Vol. 44, Issue 3. -P. 92-103. - DOI: 10.1007/s10527-010-9165-x


