Реализация способа снижения нелинейности модуляционных характеристик ключевого модулятора

стот (ФНЧ) на основе непосредственной фильтрации импульсов ШИМ и преобразования ШИМ в АИМ с последующей фильтрацией ФНЧ. Предлагается реализация способа преобразования модуляцией с восстановлением исходного модулирующего сигнала на другом уровне мощности.

ОЦЕНКА ТОЧНОСТИ ДЕМОДУЛЯЦИИ ШИМ-СИГНАЛОВ МЕТОДОМ

ФИЛЬТРАЦИИ

Системы, использующие ШИМ, относятся к классу систем, в которых осуществляется дискретизация непрерывного входного сигнала по времени. В результате этого непрерывный полезный модулирующий сигнал (ПМС) заменяется последовательностью выборок, т. е. решетчатой функцией, когда зависимость выходного сигнала от входного существует только в одной точке каждого интервала дискретизации.

Для дальнейшего преобразования используется не собственно ШИМ – последовательности, а некоторая непрерывная полезная составляющая (ПС), выделенная из нее и с определенной точностью отображающая непрерывный ПМС. В этом смысле системы с ШИМ относятся к классу квазинепрерывных систем, т. е. систем, входные и выходные сигналы которых непрерывны, а промежуточные дискретизированы. Основная проблема, решаемая в таких системах – это выделение ПС, искаженной дискретизацией.

Ввиду нелинейности процесса модуляции, особенно когда для увеличения динамического диапазона (отношение максимальной входной величины к порогу чувствительности системы) используют большую глубину модуляции и методы линеаризации практически не применимы, целесообразно проводить анализ искажений

ПМС путем вычисления спектров модулированной последовательности импульсов на выходе модулятора.

Спектры различных видов ШИМ отличаются между собой и имеют достаточно сложную структуру, однако каждый спектр содержит полезную составляющую и ряд других составляющих, в том числе комбинационные, а также гармоники несущей и полезного сигнала.

В случае детерминированного модулирующего сигнала будем полагать, что на входе модулятора действует гармонический сигнал x ( t ) = U c sin( Q c t + ф ) . Такой подход позволяет качественно и количественно с большой степенью точности оценить преимущества и недостатки методов модуляции.

Основной задачей демодуляции является выделение исходного сигнала из сформированного ШИМ-сигнала. Ошибка, определяющая точность демодуляции в предположении идеальности модулятора и канала связи, зависит от вида и параметров модуляции, метода демодуляции, а также от метрологических параметров демодулятора.

Из частотных методов демодуляции различают, в основном, два [2]:

• -    метод непосредственного выделения из спектра полезной составляющей путем фильтрации с помощью ФНЧ;

• -    метод, использующий предварительное преобразование исходного вида модуляции в другой с последующей фильтрацией с помощью ФНЧ.

Метод непосредственного выделения полезной составляющей (ПС) из ШИМ-последовательности наиболее прост и применим для демодуляции всех видов синхронной ШИМ, а также некоторых автоколебательных ЧШИМ. Роль демодулятора в этом случае выполняет ФНЧ, имеющий даже в случае своей идеальности на выходе не только ПС с частотой Ω c , но и все составляющие, для которых справедливо неравенство:

|m ® 0 — P ^Q c | ^ ® гр ^, где | m ® ₀ — p Q c |, m =1,2^; р =0,1,2... - левые полосы комбинационных искажений, ® ₀ - угловая частота несущей. Таким образом, идеальный ФНЧ также приводит к возникновению методических ошибок демодуляции.

Для реального ФНЧ, имеющего передаточную функцию H (j® ), на выходе будут присутствовать теоретически все составляющие спектра, но с разными амплитудами, зависящими от АЧХ ФНЧ |H(j® ) |. Величина гармоник полезного модулирующего сигнала (ПМС) пропорциональна | H(jQc) |, величина комбинационных составляющих - | H[j'(m®0 ± pQc)] |. Наличие указанных составляющих на выходе реального ФНЧ и обуславливает среднеквадратические искажения ПМС (СКИ). Кроме того, неидеаль-ность ФНЧ в полосе пропускания приводит к появлению частотных искажений, которые можно характеризовать разностью (1— | H(j® ) |). Частотные искажения в отличие от среднеквадратичных искажений могут быть скорректированы амплитудно-частотным корректором, нормированная передаточная функция которого | Hk (j®) | такова, что в полосе пропускания ФНЧ | H(j®)Hk (j®) |= 1.

Идея метода, основанного на предварительном преобразовании одного вида модуляции в другой, состоит в подборе вида модуляции, при использовании которого уменьшалась бы методическая ошибка, либо она вообще отсутствовала [2]. Из теории импульсной радиосвязи известно, что амплитудно-импульсная модуляция (АИМ) при коэффициенте следования ц = ® ₀ / Q макс >  2 не создает рассматриваемой методической ошибки, так как в этом случае в спектре содержатся составляющие с частотами Q c , ® ₀ и ( m ® ₀ ± Q с ) . Следовательно, используя перед демодуляцией с помощью ФНЧ преобразование ШИМ в АИМ, можно повысить точность демодуляции при условии, что для конкретного вида АИМ и ШИМ такое преобразование не приводит к появлению дополнительных спектральных составляющих, т. е. отсутствует методическая ошибка преобразования.

Отсутствие методической ошибки при двойном преобразовании возможно, если соблюдать два условия одновременно:

• -    амплитуда импульсов у АИМ должна соответствовать согласно определению АИМ значению ПМС в моменты окончания этих импульсов t к ;

• -    по определению импульсы АИМ должны быть “расставлены” через одинаковые промежутки времени, равные одному такту T ₀ .

Данные условия соблюдаются при преобразовании ШИМ-2 в АИМ-2. Так как при АИМ выборка берется в момент времени nT ₀ на протяжении тактового интервала, то первое условие будет выполнено всегда. Второе условие выполняется, если формировать импульсы – АИМ-2 со сдвигом на такт, т. е. в моменты ( n + 1) T ₀ , используя, например, ГПН, запускаемый в момент t к ′ . Таким образом, преобразование ШИМ-2 в АИМ-2 может не вносить методической ошибки. Для этого найдем спектр ШИМ-2 сигнала, преобразованного в АИМ-2.

При использовании однотактной односторонней широтно-импульсной модуляции второго рода (ООШИМ-2), функция, описывающая модулируемые срезы импульсной последовательности, имеет вид:

tK = nT0 + t 0 + T 0 +

+ ^Дт m sin[ ^Q c ⁽ t 0 + ⁿ T 0 + ^T o ) + Ф ^] , (1) где t ₀ - начальная фаза немодулированной импульсной последовательности; т ₀ - длительность немодулированного импульса; Д т _m - амплитуда временного смещения импульса под действием гармонического входного сигнала ( Дт _m = x ₀U_c , где U_c - амплитуда входного сигнала; x ₀ = tg a ₀ , а ₀ - угол наклона пилообразного напряжения), Q c , ф - частота и начальная фаза входного сигнала. Тогда к моменту ( n + 1) T ₀ , когда формируется АИМ-2 импульс, его амплитуда будет равна:

А к = x [( n + 1) T 0 + t 0 - t'_K ] где x – наклон пилы.

С учетом (1) для A к получим:

A k = x ^{[ т} 0 - ^Дт m ^{sin( Q} c tк ^{+ 0} c ^)] - ⁽²⁾ где t к = t 0 + ^nT 0 ; 0 c = ф ^{+ Q} J 0 .

Полученная импульсная последовательность имеет вид:

«

F ( t ) =      +           sin( ₄t + 0 ) +

T 0          T 0

• ⁺    S ^I¹ g ⁽ m ^ 0 ^)|cos( m ® 0 t ^{+ 0} m 0 ) ⁺

m = 1 ^T 0

M

⁺ — ¹ g ⁽ m ® 0 ^{+ Q} c > ^cos|( m ® + ^Q c )t ⁺⁰ m _{| +} 1 ^{] 1}

-

M

-^ ^{a 1} g ^{( т} ^ ) ^+Q c )l ^COs[ m q >^-Q c )t ⁺⁰ m - 1 ^]} , (4) где © c = Ф + ^Q c ^T 0 + arg g ^{( Q} c ) ;

• ⁰    m 0 = ^- m ® 0 t 0 - arg g ⁽ m ^ 0 ) ;

• ⁰    m + =- m ® 0 t 0 ± ® c ^T 0 ± Ф — arg g ⁽ m ® 0 ± ^Q c ) _;

g (c - j ) - комплексная спектральная функция производной фронта импульсов.

Из (4) видно, что спектр сигнала ШИМ-2, преобразованного в АИМ-2, не содержит гармоник ПМС и не приводит к появлению дополнительных спектральных составляющих, т. е. использование преобразования ШИМ-2 в АИМ-2 не приводит к увеличению среднеквадратичный коэффициент искажений (СКИ) сигнала. Сиг- нал вида (4) демодулируется с помощью ФНЧ, СКИ в соответствии с (4) составит [2]

Л2

K f =& m I H[j ( m ® ±Q c 'll² ! I| H ( j Q. )l . (5) l m

Условие отсутствия частотных искажений в полосе пропускания будет соответствовать в простейшем случае условию | H ( j ® ) | = 1 . Приведенные аргументы доказывают, что использование преобразования ШИМ в АИМ для повышения точности демодуляции (или частотного диапазона при заданной точности) не вносит дополнительной методической ошибки только при ШИМ-2.

Таким образом, преобразование ШИМ сигналов в АИМ – сигналы в процессе демодуляции и последующая фильтрация обычным ФНЧ позволяет избавится от ошибок, характерных для демодуляции ШИМ-сигналов посредством фильтров [2, 3]: при ШИМ максимальные значения K f достигаются в области частот, лежащих в середине полосы пропускания системы, и проектирование систем дол ж но базироваться на зависимости K f ( Ц ) при Q « 0,4 ^ 0,5 ; основной вклад в значение K f при ШИМ вносят гармонические искажения (вторая и третья гармоники ПМС), причем с ростом порядка фильтра удельный вес гармонических искажений растет по сравнению с комбинированными, где Q = Q _c I Q срф . Спектральные характеристики АИМ-сигналов, полученных после преобразования ШИМ – АИМ, являются более благоприятными с точки зрения выделения непрерывной ПС или модулирующего сигнала x ( t ) .

Подобный способ преобразования модуляцией приводит к последовательности АИМ-им-пульсов, амплитуды которых несут информацию о значениях модулирующего сигнала в тактовые моменты времени. Несомненным достоинством использования указанного метода преобразования модуляцией при демодуляции ШИМ-сигналов является увеличение амплитуды ПС выходного сигнала (после расширения импульсов АИМ на весь тактовый интервал) вне зависимости от применяемой глубины модуляции.

На рис. 1 иллюстрируется способ преобразования модуляцией, снижающий методическую ошибку Здесь f (t) - последовательность импульсов с выхода ШИМ, модулирующего сигнала по условию модуляции второго рода; 5* (t) -значения модулирующего сигнала в тактовые моменты времени; x (tn ) - АИМ-импульсы с ординатами

tn x (tn) = - J 5 (t)dt tn 0

, несущими ин-

формацию о значениях модулирующего сигнала в тактовые моменты времени.

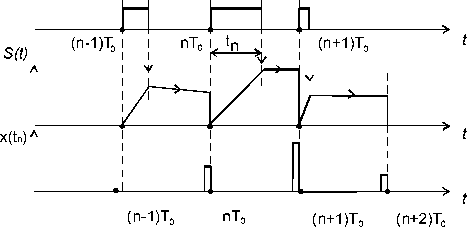
Рис. 1. Иллюстрация способа преобразования ШИМ-2 в АИМ-2

Практическая реализация ключевого модулятора. В силу указанных выше факторов были экспериментально исследованы две системы преобразования модуляцией для линеаризации характеристик по огибающей их выходного напряжения, различающиеся схемой построения силовой части. Первая схема представляет собой составной импульсный преобразователь [4] с системой управления по среднему значению входного напряжения второй части конвертера и максимальному току ключа и дополнительным контуром регулирования по огибающей выходного сигнала (рис. 2).

Во второй схеме реализован широко используемый в радиовещании конвертер понижающего типа (рис. 3), особенностью которого является то, что его силовые элементы дополнены дросселем по входу преобразователя.

Цепи ООС по току и напряжению каждой системы, кроме линеаризации регулировочной характеристики регулятора, служат также для компенсации погрешностей цепей формирования широтно-модулированных сигналов и устраняют составляющие пульсаций выходного напряжения.

Метод замкнутых контуров при использовании стандартных измерительных средств является [5] наиболее эффективным и экономичным

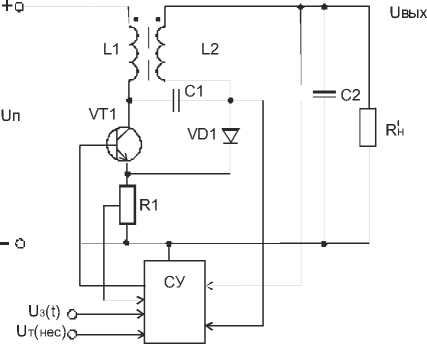
Рис. 2. Система ШИМ-сигналов с использованием составного импульсного преобразователя

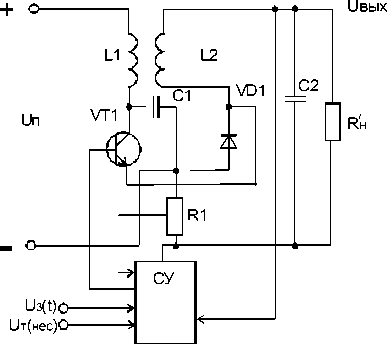
Рис. 3. Система ШИМ-сигналов с использованием преобразователя понижающего типа при определении качественных показателей ключевых модуляторов. Основные характеристики преобразователей наилучшим образом могут быть установлены посредством определения их амплитудно-частотной характеристики (АЧХ), коэффициента усиления и фазы желательно для случая, когда система управления имеет свою нормальную конфигурацию, т. е. когда обратные связи замкнуты.

Для экспериментального определения качественных показателей типов ключевых модуляторов на рис. 4 представлена схема экспериментальной установки, с помощью которой стандартными приборами производились замеры входных и выходных параметров. С помощью выходного ФНЧ подавляются составляющие тактовой частоты, в результате на эквиваленте нагрузки R H ′ выделяется усиленное модулирующее напряжение звуковой частоты.

На рис. 5 приведены качественные показатели ключевых модуляторов: неравномерность Δ Y амплитудно-частотной характеристики (АЧХ), выраженной в децибелах (дБ), и уровень нелинейных искажений ( K Г ) огибающей их выходных сигналов, выраженный в процентах (%). Источник тестовых сигналов, состоящий из постоянного и переменного сигналов Uз ( Ω ) поступает на СУ силового преобразователя, работающего в режиме слежения и повторяющего эти сигналы на другом уровне мощности. На рисунке 5 а, б представлены зависимости Δ Y и K Г от частоты задающего сигнала понижающего и составного вариантов регуляторов-модуляторов соответственно.

Сравнивая результаты замеров Δ Y двух типов преобразователей можно отметить незначительный разброс неравномерности их АЧХ в обеих сторонах от центральной частоты огибающей U ₃( Q ) - 1000 Гц. Зависимости уровней нели-

Силовой преобразователь

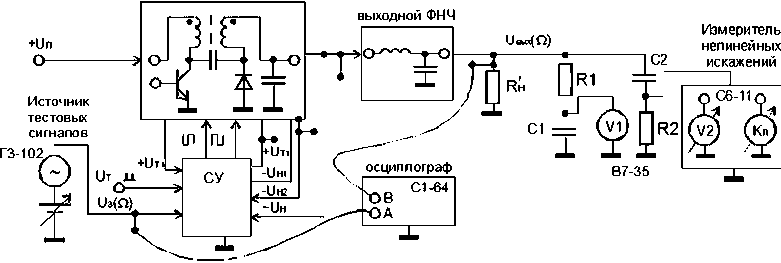
Рис. 4. Стенд для определения качественных показателей ключевого модулятора

методом замкнутого контура

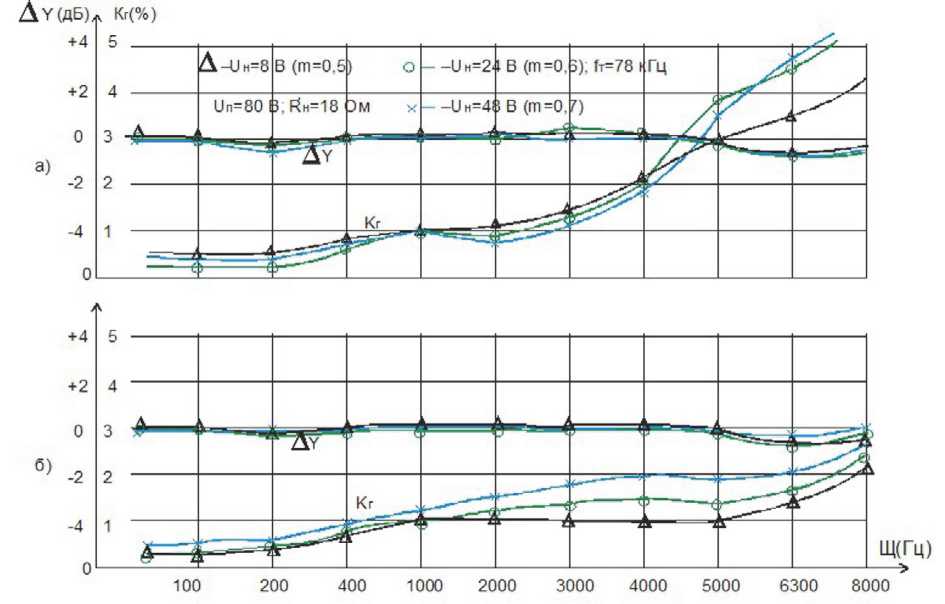
Рис. 5. Качественные показатели типов ключевых модуляторов

нейных искажений от значений частоты огибающей задающего сигнала, а также уровня этого сигнала, значительно отличаются друг от друга.

Полученные результаты экспериментальных исследований сравниваемых ключевых модуляторов позволяют сделать выбор в пользу варианта с составным импульсным преобразователем.

ВЫВОДЫ

• 1.    Ошибки, определяющие точность демодуляции систем с ШИМ методом фильтрации, возникают по двум причинам: появление высокочастотных гармоник за счет импульсной модуляции, а также комбинационных гармоник, попадающих в полосу пропускания фильтра; частотные искажения самого полезного сигнала, вызванные, с одной стороны, неидеальностью характеристик

• 2.    Доказано самим принципом преобразования в ключевом модуляторе, построенном по гибридной топологии силовой части, что спектральные характеристики, после преобразования ШИМ-АИМ, являются более благоприятными с точки зрения выделения непрерывной полезной составляющей (ПС) модулирующего входного сигнала x(t). Преимущество данного преобразования состоит в простоте технической реализации и увеличении амплитуды ПС выходного сигнала вне зависимости от применяемой глубины модуляции.

• 3.    Проведенные экспериментальные исследования модификаций ключевых модуляторов позволяют утверждать, что энергетические возмож-

• ности рассмотренных схем практически равноценны. Однако, почти одинаковые энергетические возможности не означают равноценности схем по их основному показателю – коэффициенту нелинейных искажений огибающей выходного сигнала. Главное различие заключается в условии работы ключевых элементов и фильтров.

ФНЧ в полосе пропускания, а с другой – дополнительными искажениями, обусловленными конечной скважностью импульсов АИМ.