Реальный мир и проблемы его моделирования

Познание окружающего нас реального мира происходит посредством наших ощущений, в их самом широком смысле, и моделируется в индивидуальном и общественном сознании в виде образов-моделей сущности. Каждый образ имеет свой атрибут, свою самоорганизацию, структурную определённость и эволюцию, что обеспечивает их качественное и количественное многообразие. Погружение в мир моделей служит необходимостью ориентации в реальном мире.

Одним из фундаментальных методов анализа и моделирования в процессе познания служат математические методы. Математические объекты используются в анализе явлений химии и биологии, психологии и медицине, экономике, социологии, педагогики и языкознания и интерпретируются как материальные объекты. Здесь конструктивные приёмы сформированы эволюцией человеческого мышления и опираются на методы классической механики как основы физической интерпретации реальности. В классической механике отсутствуют операции с реальными объектами. Её элементами являются абстрактные алгебраические и геометрические образы, например, масса, объём, импульс, скорость, ускорение и сила – суть числа и системы чисел. Гносеологические корни материи как философской категории объективной реальности, отражает не только гармонию самой природы, но и характеризует математическое единообразие описания эволюции на всех уровнях её самоорганизации. Здесь находят своё место и взаимоотношения людей. В реальной жизни эти взаимоотношения формируют индивидуальные особенности самого человека, формируют межличностные и экономические отношения, трудовые коллективы, различного рода промышленные и финансовые организации. Взаимодействия могут носить моральную, физическую, психологическую, юридическую основу. Реальные объекты отражаются в механике в образах в скалярной, векторной, тензорной форме - в форме различных числовых массивов; эволюция описывается полевыми теориями, поскольку полевая переменная формально в классической механике рассматривается как пространственная координата, а в квантовой механике - как оператор. Здесь оператору отвечает наблюдаемая - массив данных. Обычно элементом массива служит прямоугольная матрица, состоянию соответствует вектор, а инструментальным аппаратом служит гильбертово пространство, в котором наблюдаемой ставится в соответствие самосопряжённый оператор A, состоянию (чистое) - векторы ф, у = Аф, среднее значение наблюдаемой определяется мерой

а = р(-ф,р') = (р,^) = Р*"Ф = < р[Ф >= р*Ар = < р|А|р >,

а динамическая эволюция - заданием самосопряжённого оператора H такого, что

А ^ At = eitHAe-ltH или р ^ р( = е-инр.

Примером математического образа реальной региональной финансовой системы может служить отчётность её действия в виде массива числовых таблиц.

Если обратиться к интерпретации движения капитала «товар - деньги - товар» видим, что в основе любого бизнеса лежит колебательный процесс. Оценки колебательного процесса лежат и в управлении качеством. Но здесь можно наблюдать и монотонное вращение, монотонное отклонение наблюдаемой от её базисного положения при отслеживании превышения допустимых пределов, например, по контрольным картам Шухерта. Обычно, эволюция представляется наложением трансляции, вращения и колебания,

Н = НТр + НВр + Якол где любая составляющая может быть пренебрежимо мала.

Обращаясь к экономической задаче видим, что любой бизнес -циклический процесс, который предполагает закупку ресурсов q, их предпродажную подготовку и реализацию готовых товаров по рыночным ценам p. Цена реализации служит импульсом бизнес-начинаний движения капиталов, которое представимо аддитивно факторизованной функцией

H = Т(р) + V(q),

где первое слагаемое

Т(Р)=РЧ,  4=^

определяет кинетическую часть капитала – выручку от реализации товара.

Для упрощения постановки задачи предполагают, что продажи пропорциональны ценам. Второе слагаемое является функцией остатков, зависит от продаж q и определяет нереализованные возможности товарооборота. Для оптимизации функции H нужно найти компромисс между максимизацией выручки T и минимизацией остатков V . Задачу можно рассматривать как биматричную игру, если ввести стохастические векторы стратегий продаж и управления остатками α и β и записать её в виде

H = a*W0 = (a,W0).

Выручка от реализации товара вместе с нереализованными возможностями в классической механике будет функцией H , которая является гамильтонианом одномерного гармонического осциллятора. В квантовой механике ей будет отвечать оператор Гамильтона. Если ввести новые метрические функции

*=$■ ,    ^v = ^p^ ,               (2)

то равенство (1) принимает вид H = hσ ²/2, где новая мера в правой части введена основным метрическим тождеством Пифагора

с2 = [i2 + (v/h)2,                            (3)

в котором величина h служит масштабным коэффициентом соизмерения (2).

Определим сопряженные бозе-операторы

_ ц+iv/h    в* _ ц-iv/h

42  , D =  42, удовлетворяющие коммуникационному отношению [B, B*] =1. Их произведением введём операторы A = BB*, Λ = B*B. Приходим к представлению

Н = ^(А + Л),(4)

а коммуникационное тождество принимает вид ( I – тождественный оператор)

А-Л = 1.(5)

Пусть функция φ является произвольной собственной функцией оператора H и E – отвечающее ей собственное значение

Н(р = E(p.(6)

Из условий (4) - (6) имеем

А( = (^ + 1)P,     Лр = (^- 1)p.

т.е. операторы H, Λ и A имеют одну и ту же последовательность собственных функций. Из второго равенства (7), учитывая, что Aφ >  0, находим, что минимальная изоэнергетическая поверхность описывается уравнением

Н = h, что отвечает собственной функции φ0 оператора Λ с минимальным собственным значением, равным λ = 0. Поскольку операторы (7) вместе с гамильтонианом (4) имеют одну и ту же последовательность собственных функций, то они коммутируют друг с другом и если λ произвольное собственное значение оператора Λ, а a – собственное значение оператора A, отвечающее той же собственной функции, то a = А + 1. Их последовательности суть арифметические прогрессии с равной единицы разностью. Поскольку эти операторы эрмитовы, то, если ранг оператора Hравен п, то А = 0, 1, ..., n -1 -последовательность собственных чисел оператора Л, а a = 1, 2, ., п -последовательность собственных чисел оператора A. Изоэнергетические уровни гармонического осциллятора H будут определяться формулой

Ej=1(2j-1)h, 7 = 1,2.....п.               (9)

Следовательно, масштабный множитель соизмерения мер (2) заключает в себе минимальную условную единицу капитала, необходимого для перехода с одного изопотенциального уровня на другой. Если функция щ описывает осцилляционный процесс, то она удовлетворяет уравнению

Вщ = by.                                (10)

Бозе-оператор B не эрмитов и множитель b может быть комплексным.

Решение (10) ищем в виде разложения по собственным функциям ф_к ( к = 1, 2, ., п ) гамильтониана H : ф = ^С_к. Используя рекурсию В (к = ^ксРк—1, получаем Вф = ^С_к^к(_к-1 = ^С_к+1^к + 1(_к.

С учётом равенства (10) находим рекурсию для искомых коэффициентов и выражения для коэффициентов посредством её первого коэффициента

h                      Я^

Ск = ^кСк-1  Ск = ^к!Со'

Получаем

■ = С0^

ь ^к

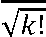
(к.

Здесь постоянный множитель определяется нормированием и при п ^ ю приближённо равен С₀ = е ^-ь 2 ^/2 . Если осциллятор в стационарном состоянии ф_к находится на энергетическом уровне E k , то

Р(к) = \(ф,(к)\2 = ^-е Ь2, к!

т.е. энергетические уровни распределены по закону Пуассона с параметр b ².

«Экономика и социум» №2(33) 2017