Recognizing Bangla handwritten numeral utilizing deep long short term memory

Handwritten numeral recognition (HNR) has gained much attention in present days due to applicability in range of tasks. HNR is useful in diverse fields including number plate identification, optical character recognition, passports and document analysis, fraud detection, postal system automation, automatic bank cheque processing [1]. Prior to this research, a bulk of works has been done on unconstrained HNR with state-of-the-art progress in Arabic, Chinese and scripts [1, 2, 3]. On the other hand, research on Bangla HNR (BHNR) is far behind although it has ranked 7th in the list of languages based on native speakers [4]. Moreover, it is the official and most broadly talked dialect of Bangladesh and second most generally spoken out of the 22 planned dialects of India. Bangla contains similar shaped numerals which are difficult to distinguish even in printed form and this makes BHNR a challenging task. Therefore, effort with new techniques for better BHNR is essential and a demand of time.

A few studies are available for BHNR using artificial neural network (ANN) as ANN is a prominent tool for classification task which is a common step in any recognition system. Khan et al. [5] investigated a MultiLayer Perceptron (MLP), i.e., three layer ANN, based method for BHNR. It uses horizontal and vertical scanning along with boundaries extraction to extract a numeral within a single window; and following this, applied scaling to reshape them into a fixed sized matrix. Finally, it uses this data to train an MLP for recognition purpose. et al. [3] proposed a BHNR framework, where they utilized Dempster-Shafer method for reasoning of uncertainty within various classes and later combined the classification choices of two MLP based classifiers utilizing shadow as well as centroid feature sets.

Finally, using those features, they performed recognition via an SVM classifier.

Apart from the works discussed above, there is a class of models which have been designed based on non-neural network-based assumptions. Bashar et al. [11] adopted a manual hand-crafted feature-based framework where, they first created histograms from the uniform features of the scanned image and later predicts the appropriate class decision based on the shape and region of this histogram. Pal et al. [2] proposed a BHNR framework where they adopted an interesting feature extraction method called: “water overflow from the reservoir” and finally initialized a binary tree classifier for the classification. Recently, researches are also working with kernel and bayesian discriminant based methods for these kinds of supervised problems [12].

Most recently, deep neural network (DNN) have been successfully applied in many pattern classification task showing great potential in mimicking the hidden elements of the information through its profound design. Among several DNN models, convolutional neural network (CNN) has been very popular because of many state of the art performance for image classification task over traditional NN based approaches. Akhand et al. [10] investigated a CNN based BHNR technique in which they prepared a two layer CNN with the standardized dark scale estimation of picture pixels as the components and utilize a completely associated NN at the final layer to anticipate the class.

The goal of this study is to build up a superior BHNR system and in this course, we consequently examined profound architecture of Long Short Term Memory (LSTM). LSTM is very good with sequence data with its gating and carry mechanism through series of time steps. It effectively finds out sequence alignment and do not need any segmentation of data. In this study, deep architecture of LSTM is considered for BHNR because DNNs perform superior to single layer networks for speech recognition [13].

The investigated deep LSTM based system of this study comprises of two LSTM layers, trailed by a reshape layer, a dense layer and lastly the output layer. Handwritten numeral images are normalized first; then sequenced and after that, LSTM is used to characterize singular numerals. Unlike other related works it doesn't utilize any feature extraction technique. Benchmark dataset with a large number of handwritten numeral images is utilized to recognize the adequacy of the proposed technique. In order to highlight the significance of deep architecture, a single layer LSTM model was likewise tried on the similar corpus. It is observed that deep LSTM gives higher recognition accuracy than single layer LSTM. Our extensive experiments reveal that the proposed deep LSTM based method shows state of the art classification performance outflanking some very good existing methods.

The rest of the paper is sorted out as follows. Segment II clarifies the BHNR system introduced in this work utilizing profound LSTM which likewise consists of dataset readiness and preprocessing. Segment III presents the experimental outcomes of the proposed framework along with in depth performance analysis against other related works. At last, a concise conclusion of the work is given in segment IV.

II.    Bangla Handwritten Numeral Recognition Using Deep Long Short Term Memory

Any HNR classification system contains two major steps: processing the handwritten images to generate patterns and then employ classifier for recognition purpose. Since LSTM is considered as base in the proposed BHNR system, at first a brief review of LSTM is presented. Then dataset preparation and proposed LSTM based architecture are described.

• A.    Long Short Term Memory (LSTM)

LSTM is a variation of recurrent neural network (RNN). RNNs are the best known and most widely used NN model for sequence data as they go over the entire sequence through time, remembers it in a compressed form and thus gains the ability to model contextual information via this recurrent connections. As a result, if the number of hidden layers in RNNs are increased, the error signal decreases exponentially depending on the number of hidden layers and this does make the training of the front layers very slow [15, 16, 17]. On the other hand, it requires a post-processing stage to get the class conditional probabilities of consecutive labels as RNN produces localized classification. Thus several limitations are faced in handling sequential labeling problems like handwriting recognition (sequence version), speech recognition and several others using RNNs. Moreover, like other ANNs which use gradient based learning methods, RNNs also suffers from vanishing gradient problem. Therefore, LSTM is considered for BHNR in this study which effectively used in sequence ordering with its distinct features.

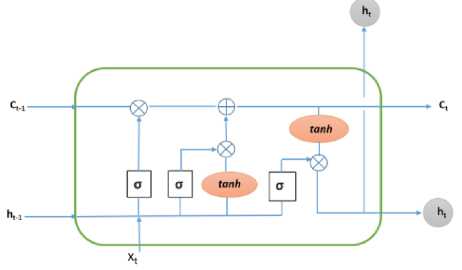
Fig.1. Structure of an LSTM cell.

Figure 1 shows the structure of an LSTM cell [16] comprising of different gates and units. LSTM acts as a memory unit and remembers a value for an arbitrary length of time. In addition, it likewise can get to long range dependencies, learn sequence arrangement and work without the need of any fragmented data. Each LSTM block contains three nonlinear gates: input gate, output gate and forget gate. These three multiplicative gates operate in such a way so as to determine whether the input is important enough to remember or forget the value by activating the forget gate. Thus the memory cells remember the error without perishing till the forget gate is activated resulting in the prevention of error decay.

An LSTM cell keeps track of values for either long or brief lengths of time as recurrent unit acts is its basic. LSTM uses a feedback loop between its hidden and cell states for each time step without any activation function which allows the stored values to not get vanished during backward pass via Backpropagation through time (BPTT) algorithm [14]. In a network with LSTMs, an LSTM cell takes previous cell state along with the hidden unit values from the previous time step as input and generates the current cell state as well as the current hidden unit values as output based on the forget gates. The network works in two passes - forward pass and backward pass. Based on the data as well as the extracted features, forward pass initializes the network parameter values and activates the hidden layer from the external input as well as hidden LSTM layer activations from the previous time step. During forward pass, an LSTM layer decides whether to keep an information completely or forget it through a sigmoid layer. It takes h_t and x_t as input and provides an output (0~1) for each number in the cell state C_t-1. If its’ output is 1, it will keep the data completely, while for 0 it will forget the data.

f t = a(W_f[h_t-_vx_t] + b_f), (1)

In the next step, it decides what kind of new information it would store in its current cell state by first initializing a sigmoid layer and then via a tanh layer which decides the values to update as well as to forget. The following tanh layer generates a vector of new candidate values Ct as follows, it = a(Wt * ht—i +Wt* Xt+ bt) (2)

C t = tanhXW c * h t-1 + W_c * X t + b c ) (3)

In the next step, LSTM combines these two and updates the cell state from C_t-1 to C_t . At first, the previous cell state value is multiplied by the forgetting factor f_t, that makes the LSTM to forget the data and then this value is added with i_t * C t to produce the new candidate values

C t = f t * C t-i + i t * C t (4)

In the output state, the output would be the filtered version of the cell state. The output is generated in two steps. In the first step, a sigmoid layer decides/selects a part of the cell state that would be presented as the output. In the second step, the selected cell states are passed through a tanh and multiplied by the output of the sigmoid gate. The selected cell states are values are squashed between -1 and 1 through a tanh layer.

O t = ^(W o * h t-i + W_o * X t + b o )      (5)

h t = O t * tanh(C_t)                (6)

In the backward pass, our model figures out the set. The gradients through BPTT algorithm [14] is applied over each of the network parameters to overhaul the system parameters thereby pushing the network towards generalization.

• B.    Bangla Handwritten Data and Processing

  HNR is language specific and a rich dataset is essential to test a system. This study uses the benchmark handwritten numeral image dataset kept up by CVPR unit, ISI, Kolkata [6]. Several recent studies have built their evaluation framework utilizing this dataset as a source [10]. The dataset obliges 23392 example numeral images with an expansive assortment of distinct samples by different people having different writing styles. The samples are the examined images of postal mail pin codes. The pin codes are from assorted individuals with various age, sex and additionally training level. The sample images are separated into training and test sets. Test set contains total 4000 sample images (having 400 examples for every one of 10 digits) whereas training set consists of total 19392 sample images (having around 1900 samples of each individual digit). Fig. 2 exhibits few example images of each numeral.

Preprocessing of images and generating patterns are the common steps of numeral recognition from handwritten images. Originally the images are in various shapes, resolutions and sizes; therefore, in order to make these raw image samples fitting into classifiers, a novel preprocessing strategy on Matlab2015a is considered. Fig. 3 demonstrates the essential strides of pattern formation from the scanned image samples. In the initial step, pictures are changed over to grayscale where each of the pixels value is a solitary whole integer within the range of 0 to 255. This integer value speaks to the brightness of the pixel. Regularly, integer value of 255 speaks to a white pixel where value 0 speaks to a dark pixel. In order to reduce the computational complexity, these sample images are changed from grayscale to binary format having just 0 and 1 values with a controlled threshold. This progression removes the background and also enhances intensity. Since dark pixels are plotted on the white paper for the composition of a numeral, the resulting sample binary image contains comparatively a large number of 1’s than 0’s. So to have more 0’s than 1’s, the foreground and background colors are interchanged resulting in a very huge gain in terms of computational complexity. The dark lines from each of the four sides (i.e., left, right, top and base) are expelled by cropping an image to the genuine written portion. The image files evaluated here are frequently found in various sizes for distinctive writing style various people. To keep up proper and equivalent contributions for every one of the numerals, the subjective images are resized into 28×28 measurement. To catch pattern estimations of resized

English Numeral	Bangla Numeral	Sample Handwritten Numeral Images
0	০	0	0	9	6		0	Cd	0		0
1	১		ъ				c)	Э		>
2	২
3	৩				о				V9
4	৪		g	g			&		к
5	৫		S'			Or	G				(7
6	৬			IS-							U,
7	৭		4	r
8	৮	lr-	F			(r*	Xt^		b*^	^^ ^*
9	৯	4	<5

Fig.2. Sample images from benchmark Bangla handwritten numeral dataset.

Scanned handwritten numeral

(1) Transform into binary image

(2) Foreground-background interchange

(3) Cropped to actual writing portion

(4) Resized into 28x28 pixels

(5) Transform into sequences

Pattern for classification

Fig.3. Steps of pattern formation from scanned handwritten numeral.

images as well as to hold most ideal quality of them, float64 matrix is considered instead of the binary images as done in the past stages.

As LSTM is a sequence learning method, it is necessary to transform these handwritten numeral images into sequences before feeding them. In this study, 1-D pen stroke sequences have been used for this transformation. The image samples were thresholded and thinned using above procedure, yielding single-pixelwidth digit skeletons. Finally, sequences of pen movements were determined generating those digit skeletons., Fig. 4 presents the stepwise outcome of the transformation on several images (0 to 2) which gives a better insight about what’s happening inside those stages.

• C.    Deep LSTM based BHNR

Figure 5 shows the network structure for BHNR based on deep LSTM (BHNR-DLSTM) considered in this study. The network consists of an input layer, two LSTM layers, a reshape layer, a dense layer and finally the output layer. As HNR is a classification task, in a LSTM layer (i.e. hidden layer), each of the LSTM cell is considered as a hidden unit likewise in a typical ANN. LSTM units are consistently realized in "blocks" containing a couple of units which is typical with "deep" multi-layered ANNs and this does influence the architecture to be implemented with parallel settings. First LSTM layer contains 100 LSTM cells and the second one contains 50 LSTM cells. The outputs of the LSTM layers are connected to a feed-forward layer with tanh activation. Since generalized information is required towards final classification, lesser number of LSTM units (i.e., 50 units) are used in the deeper portion of the network. The first LSTM layer takes 28×28 sized handwritten numeral images in the sequence form as input. All of the LSTM gates are activated - deactivated based on these sequence values and the amount of information that are required to be remembered. As shown in Fig. 4, it requires 60 sequences in order to write numeral ০. Similarly, 47 and 51 sequences are required to write numeral b and 4, respectively. In order to cover up the variation of writing styles of different persons, maximum 100 units of hidden LSTM cells are used in the first layer considering that the number is enough to write a numeral. This 100 LSTM cells generate 100 hidden unit values based on the sequence of strokes in the x and y direction, end-of-stroke as well as end-of-digit. The values of these 100 units of first LSTM layer is generalized through 50 units of second LSTM layer and propagates some of these information further.

০      ১

২

Origninal image in tif format

Binary image with automatic thresholding

Forground and background interchanged

Cropped to original writing portion

Resized into 28×28 pixels

Transform into Sequences

Fig.4. Stepwise outcomes of pre-processing for sample figures from ০ , ১ and ২ .

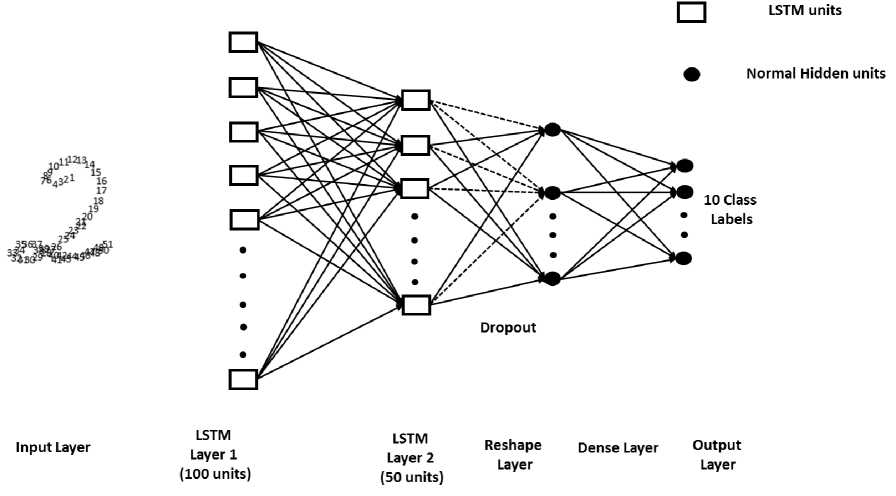
Fig.5. Proposed BHNR-DLSTM Structure.

This generalized information of second LSTM layer is further processed through reshape and dense layers for final network response. As the ratio of the training data against the complexity of the network is very high and the weights between the two LSTM layers are fully connected, there might be an overfitting. However, in LSTM, the gradient at each time step is carried out along with the gradient from several time steps before, resulting in the network to overestimate the utility of the model. In order to prevent this, dropout technique is applied before the reshape layer, with a probability of 0.2 so that in each epoch during training, 20% of the random activations in the associated layer is dropped off. However, during testing, all the activation units are kept active. Recent studies reveal that this does push the network towards generalization and make it much less likely to overfit. Following this reshape layer, there is a dense layer which flattens the output of the reshape layer by forming a 1D vector. Finally, a fully connected structure is formed between the dense layer and output layer having 10 output units representing 10 class labels. These 10 units are activated and deactivated based on their inputs; and the maximum value among these 10 units represent the corresponding class label. Any deviation from the network generated response and desired response would result in error as measured using Eq. (7).

Е = |^ £ £=1 £ п=1 (^ п (Р^)-У п (Р⁾⁾², ⁽⁷⁾

where P denotes total number of patterns and N denotes number of output nodes; y n (p) and d n (p) are actual and desired output of n th node for p th pattern, respectively. During training, the weights as well as different gates are updated through BPTT algorithm in the course of minimizing this error.

III.    Results and Discussions

This section contains an extensive evaluation of the proposed recognition scheme. From the ISI benchmark dataset [6], 18000 samples are considered for training and 4000 samples are considered for testing. Samples are uniformly distributed over the fundamental 10 classes with 1800 and 400 samples per class for training and testing respectively. We reported both training set and test set results to see the how well the model fits as well as how well the model generalizes.

The preprocessed data used in the proposed BHNR-DLSTM system is not in the traditional pixel matrix form rather than it is in the sequence matrix form where each row represents a sequence. We have not performed any kind of feature extraction on the data except rearranging it as a sequence. The entire model was implemented in python utilizing deep learning framework (Theano). The analyses have been performed on MacBook Pro portable PC machine (CPU: Intel Core i5 @ 2.70 GHz and RAM: 8.00 GB) in OS X High Sierra environment.

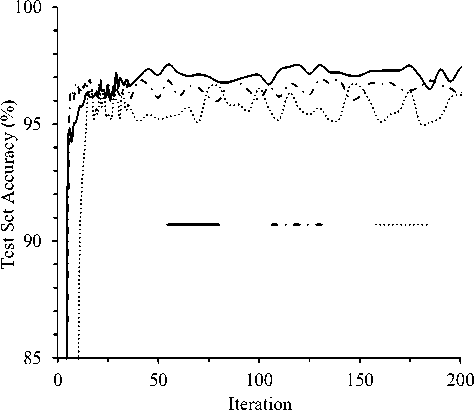
(b) Test Set Accuracy

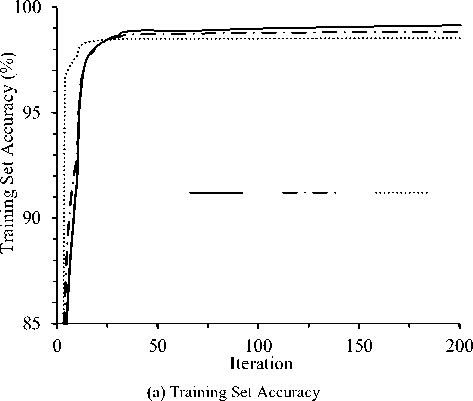
Fig.6. Effect of different architectures with LSTMs varying number of layers and LSTM units.

Figure 6 depicts the effect of different architectures with LSTMs varying number of layers as well as number of LSTM units to visualize the motivation of deep architecture over single layer LSTMs. The single layer architecture consists of an input layer, then an LSTM layer followed by a reshape layer, then a dense layer, and finally the output layer. A single LSTM layer having 100 and 150 LSTM units are considered respectively for this comparison. On the other hand, the deep architecture have 100 and 50 units on the first and second LSTM layer respectively. Batch size was 100 and learning rate was 0.02 for the experiments. From the figure it is observed that accuracy of both training and test sets improved rapidly in initial iterations and improvement is not significant after certain iteration. It is clear from the figure that deep LSTM architecture clearly outperforms single layer LSTM models on both training and test sets. The figure clears the hypothesis of using deep architecture in this study instead of the single layer architecture.

Table 1 compares performance of different LSTM architectures for different batch sizes (BS) after training fixed 200 iterations. Learning rate was 0.02 for the experiments. It is notable from the table that for the fixed 200 iterations, training with BS = 50 requires remarkable time than for BS = 100 or 150 in all of the three network structures. In case of single layer LSTM with 100 units, training time for 200 iterations are 188.27, 158.74 and 131.97 minutes for BS values 50, 100 and 150, respectively. The reason behind larger time for smaller BS value is that networks updates more frequently for smaller BS values than larger BS values. However, training error (i.e., E ) is comparatively low for smaller batch size; and hence, training and test set accuracy are also found lower for smaller BS value. It is remarkable that deep LSTM outperformed any single layer LSTM with any BS value. For BS=50, deep LSTM shows training set accuracy 99.27%; whereas the values are 98.87% and 99.01% for single layer LSTM with 100 and 150 units, respectively. Similarly, test set accuracy is also found better for deep LSTM (with total 150 LSTMs in two layers) than single layer network with the very same number of 150 LSTMs in the layer. These results clearly identifies the effectiveness of deep LSTM architecture. The reason behind is that deep architecture may coincides with known patterns very quickly as well as correctly mimicking the underlying data patterns.

Table 1. Performance evaluation of different Batch Size (BS) after 200 iterations.

Architecture	Batch Size	Time in Mins	Training Error	Training Acc. (%)	Test Acc. (%)
Single Layer LSTM (100 Units)	50	188.27	0.071834	98.87	96.23
	100	158.74	0.076054	98.52	96.14
	150	131.97	0.082764	98.44	95.95
Single Layer LSTM (150 Units)	50	205.94	0.047472	99.01	96.36
	100	178.46	0.052010	98.83	96.24
	150	151.59	0.058294	98.68	96.05
Deep LSTM	50	244.36	0.010515	99.27	97.55
	100	214.86	0.012015	99.15	97.40
	150	182.73	0.012876	99.02	96.98

Figure 7 depicts the effect of learning rate (LR) on the performance of deep LSTM architecture. Experiment was conducted for three LRs 0.01, 0.02 and 0.1 for BS=50. Fig. 7(a) clearly depicts that, training set accuracy increased linearly with number of iteration in all of the three cases. But accuracy fluctuates little with respect to iteration for LR=0.1. For larger LR values, the accuracy fluctuation is common and more visible for test set accuracy. From the figure it is found that LR=0.02 with BS=50 performs best compared to all of the other configurations. This is because, smaller BS values allow the gradients to be applied very frequently and smaller LR value allows the network to take smaller steps to apply those gradients. As test set performance gives hints about model’s generalization capability, we further tested deep architecture on unknown patterns of test data with different LR values and fixed BS value of 50. The outcome is clearly visible in Fig. 7(b) and it proves that even with unknown pattern, LR= 0.02 with BS =50 gives best performance.

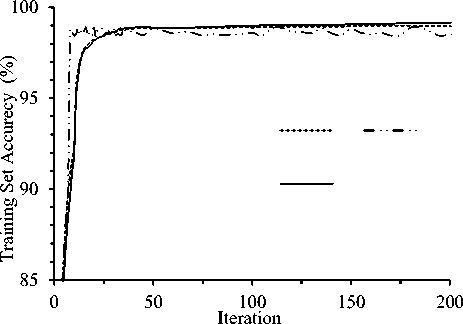
(a) Training Set Accuracy

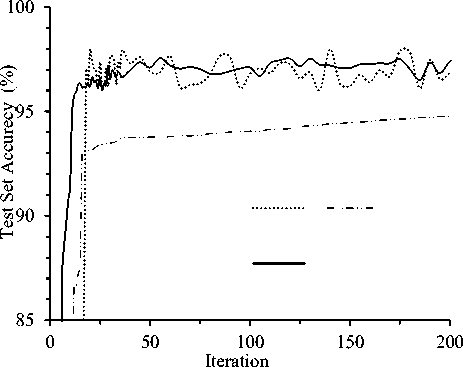
(b) Test Set Accuracy

Fig.7. Effect of learning rate (LR) on the performance of deep LSTM architecture.

Figure 8 shows the training set and test set recognition performance for BS= 50 and LR= 0.02 to identify the efficiency of deep LSTM up to 400 iterations. We have recorded recognition accuracy of the framework for a different settled number of epochs and obviously, the system began to give over 95% test set precision with just 50 emphasizes. Likewise, recognition precision improved with accentuation for both training and test sets rapidly at bringing down epoch esteems (e.g., up to 100). On the other hand, test set precision did not blend with training set performance since its cases were subtle by LSTM in the midst of training. It is certain that the precision on the test set is all the more appealing that demonstrates the generalization capacity of a framework.

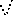
0         100

200       300

Iteration

Table 2 exhibits the confusion matrix of the test set examples after fixed 400 epochs. From the table, it is obviously noticed that the proposed strategy most exceedingly terrible performed for the numeral " ৯ " and out of 400 experiments, in 383 cases it classified that accurately. In eight cases, it is classified as " ১ ". Both " ৯ " and " ১ " have a type of obscurity fit as a fiddle. In the Bangla handwritten numeral content, " ৩ " and " ৬ " appears to be identical; in this manner in 11 cases, " ৬ " assigned as " ৩ ". Moreover, the numeral " ৫ " named " ৪ " and " ৬ " in three and four cases, respectively; it is obviously seen that these perplexities in a couple of handwritten numeral image samples are a result of various synthesis styles of individuals. Nonetheless, the proposed strategy has accomplished best recognition performance for " ২ " by effectively characterizing each one of its 400 test tests.

Fig.8. Training and Test Set Recognition Accuracy batch size 50 and learning rate 0.02.

Table 2. Confusion matrix for test samples.

English Numeral	Bangla Numeral	Total samples of a particular numeral classified as
		০	১	২	৩	৪	৫	৬	৭	৮	৯
0	০	398	0	1	0	0	0	1	0	0	0
1	১	0	382	1	0	3	0	3	0	0	11
2	২	0	0	400	0	0	0	0	0	0	0
3	৩	1	0	0	393	0	1	3	0	2	0
4	৪	0	0	0	0	399	0	0	0	1	0
5	৫	0	0	0	1	3	392	4	0	0	0
6	৬	1	0	0	11	0	2	386	0	0	0
7	৭	0	0	1	0	0	1	0	398	0	0
8	৮	0	0	0	0	0	1	0	0	399	0
9	৯	1	8	3	4	1	0	0	0	0	383

Table 3 presents some misclassified handwritten numeral image samples. Because of vast variety in composing styles, these numeral image samples are hard to characterize even by human. At last, the proposed BHNR-DLSTM incorrectly classified 70 test set samples out of total 4000 samples and accomplished precision of 98.25% on 370th iteration. On the other hand, the proposed model misclassified just 90 image samples out of total 18000 training image samples indicating precision rate of 99.50%. This demonstrates that, there is an opportunity to enhance profound LSTM training and achieve an improved execution with the proposed model.

Table 4 looks at the consequence of the proposed technique with different obvious works of Bangla handwritten numeral recognition. It also shows specific feature(s) of individual strategies. It is striking that the proposed technique did not use any feature extraction system while the greater part of the current techniques uses perhaps more than a couple of feature extraction procedures. Without utilizing any extra procedure for feature extraction, the proposed BHNR-DLSTM strategy is seemed to beat the leaving techniques. According to the table, BHNR-DLSTM achieved test set exactness of 98.25%; though, the test set precisions are 92.80%, 95.05 % and 97.93% for [2, 7, 10], independently. Test set precision of work [6] is very close to our proposed work, yet it utilized a scaled-up rendition of the first dataset which is actually 10 times bigger than the one utilized as a part of this study. Despite the way that performance comparison about here is for different datasets, the sufficiency of the proposed BHNR-DLSTM is exceptionally intriguing and recognized the limit of significant LSTM based classifier for Bangla HNR.

Table 3. Sample handwritten numerals that are misclassified by BHNR-DLSTM.

Handwritten Numeral Image	True Numeral	Image Classified as
■	৩	০
	৩	০
	৩	০
	৫	০
	৬	৫
	৬	৫
	৯	১

Table 4. Proposed BHNR-DLSTM’s Test Set Recognition Accuracy Comparison with Some Contemporary Methods.

The work reference	Feature Selection	Classification	Recog. Accuracy
Pal et al. [2]	Water overflow from the reservoir based feature selection	Binary   decision tree	92.80%
Wen et al. [7]	Principal component analysis (PCA) and Kernel PCA	SVM	95.05 %
Basu et al. [3]	Shadow feature and Centroid feature	MLPs      with Dempster-Shafer technique	95.10%
Bhattachary & Chaudhuri [6]	Wavelet   filter   at different resolutions	Four MLPs in two stages (three + one)	98.20%
Akhand et al. [13]	No	CNN	97.93%
Proposed BHNR-DLSTM	No	Deep LSTM	98.25 %

IV.    Conclusions

Handwritten numeral recognition is a high-dimensional complex undertaking and different regular systems first concentrate significant highlights from the info picture and afterward uses MLP based strategies for classification reason. This paper proposes a deep LSTM architecture for BHNR. LSTM can perceive visual examples specifically from image sequences with negligible preprocessing without any feature extraction. The proposed model has been evaluated on a quite large corpus of handwritten Bangla numerals maintained by CVPR and results have been contrasted against existing perceptible methods. The proposed model is seemed to outmaneuver the current methods on generalization ability (i.e., test set recognition accuracy) utilizing a scaled dataset. Additionally, the proposed method appears to be effective in size and calculation.