Reducing hash function complexity: MD5 and SHA-1 as examples

Published Online January 2019 in MECS DOI: 10.5815/ijmsc.2019.01.01

In this paper, we are interested in a single block of a hash function such as password verification.

Password verification is invented by Roger Needham, who stated that instead of saving all passwords as a plain-text format, we could save the hash digest of the password only.

In the recent past years, most of the secure online business is based on the username/password authentication scheme. This scheme uses the static password identification that has a vulnerability which enables people to reveal the password easily. Alternatively, the researchers proposed to use single block hash functions as an authentication scheme. In this scheme, the system saves the user password as a hash value format. The password is often concatenated with a random, non-secret salt value before the hash function is applied. Then the system can authenticate the user by comparing the entered hashed password with the stored one. Therefore, if the system verifies the user successfully, then, he can access the system. Otherwise, the system rejects the user. In case the user forgets his password, then, the system can allow him to replace the password with a new one.

The single block of hash function length is 512 bits if we remove the padding and the message size, the remaining length is 440 bits (55 characters), which is proper for password because in most cases the password length cannot exceed the 55 characters.

• 3.    Related Work

  The researchers have examined the hash functions algorithms to reduce the complexity of these algorithms. [2] Proposed an architecture level optimization technique for universal Hash Functions by using Divide-and-Concatenate approach. They found that the divide-and-concatenate technique cannot speed-up software implementations but can only improve the resistance of collision. [3] Have presented a pipelined serialized architecture for the SHA-3 candidate Keccak, which offers very low area and power consumption with acceptable throughput. Their architecture is especially attractive for lightweight applications when implemented with compact versions of Keccak [4] Have described a new family of universal hash functions geared towards high-speed message authentication. They also introduced additional techniques for speeding up their constructions by ignoring certain parts of the computation, while still retaining the necessary statistical properties for secure message authentication. [7] The authors have proposed a lightweight hash function with reduced complexity in terms of hardware implementation, capable of achieving standard security. It uses sponge construction with permutation function involving the update of two non-linear feedback shift registers. Thus, in terms of sponge capacity it provides at least 80bit security against generic attacks which is acceptable currently. [8] have established the existence of low-complexity cryptographic hash functions that compress the input by (at least) a constant factor. They construct CRH with linear circuit size, constant locality, or algebraic degree 3 over Z 2 under different flavors of the newly introduced binary SVP (bSVP) assumption. [9] The authors have proposed a lightweight hash function with reduced complexity in terms of hardware implementation, capable of achieving standard security. It uses sponge construction with permutation function involving the update of two non-linear feedback shift registers. Thus, in terms of sponge capacity it provides at least 80bit security against generic attacks which is acceptable currently. [10] The authors have proposed a novel design philosophy for lightweight hash functions, based on a single security level and on the sponge construction, to minimize memory requirements. Inspired by the lightweight ciphers Grain and KATAN, they present the hash function family Quark, composed of the three instances u-Quark, d-Quark, and t-Quark. Hardware benchmarks show that Quark compares well to previous lightweight hashes. [11] They proposed spongent – a family of lightweight hash functions with hash sizes of 88 (for preimage resistance only), 128, 160, 224, and 256 bits based on a sponge construction instantiated with a present-type permutation, following the hermetic sponge strategy. Its smallest implementations in ASIC require 738, 1060, 1329, 1728, and 1950 GE, respectively. [11] The authors presented

  the PHOTON lightweight hash-function family, available in many different flavors and suitable for extremely constrained devices such as passive RFID tags. Their proposal uses a sponge-like construction as domain extension algorithm and an AES-like primitive as internal un-keyed permutation. This allows obtaining the most compact hash function known so far (about 1120 GE for 64-bit collision resistance security). Moreover, the speed achieved by PHOTON also compares quite favorably to its competitors. This is mostly due to the fact that unlike for previously proposed schemes.

• 4.    SHA-1

• 4.1.    SHA-1 Algorithm Steps

Secure Hash Algorithm (SHA) family is the most widely used hash functions in the recent years. In 1993, The National Institute of Standards and Technology (NIST) designed and published SHA algorithm as (FIPS 180). In 1995 the NIST team discovered a weakness in SHA-0 that allow the attackers to find a collision in the hash output, as a remedy, they published SHA-1 as an updated version of SHA-0.

SHA-1 algorithm accepts an input of an arbitrary length and produces an output of a 160-bit message hash. The input block size is 512 bits that are represented as a series of sixteen 32-bit words. These 512-bit blocks enter to a message compression function in words of 32 bits (W t ) through a message scheduler [5].

The SHA-1 hash algorithm accepts an input of an arbitrary message length and produces an output of 160-bit length. This algorithm consists of four stages; each stage is divided into 20 steps.

To calculate the hash value of a given input, we can process the message input as the following five steps [5]:

Step 1: Append length of 64-bit value that represents the message length, if the message size is larger than 64bits, then find message size mode 2⁶⁴.

Step 2: Append padding bits to the message. Therefore, it can fit a size of 512-bit multiples.

Step 3: Initialize a 160-bit buffer to hold five 32-bit words.

Step 4: Processes the message in 512-bit blocks.

Step 5: The Output that is the result of the message hash.

In the next section, we show the reduced version of the compression function (single step of SHA-1).

• 4.2.    SHA-1 Compression Function (single Step)

The researchers consider SHA-1 compression function as a heart of SHA-1 algorithm. This function divides the message into 512-bit blocks and processes each block separately.

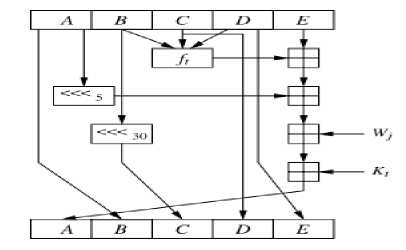
Fig.1. SHA-1 Operation (Single Step)

As illustrated in figure 1, the original SHA-1 compression function executes the following operations for each 32-bit message block to obtain the hash result:

F1 = Е + Ft (B,C,D)                                                                    (1)

New Л =

F3 + Kt

New C =

(S) << 30

F2 = F1 + (Л) « 5	(2)
F3 = F2 + Wj	(3)

Where,

• A, B, C, D, E: 32-bit buffers used to hold intermediate and final results of the hash function.

Ft: one of the three logic functions: Majority, Choice, and XOR.

W j: Single word of message block.

Kt: one of the five additives constant.

(A)<<5: Circular left shift by five bits.

+: addition modulo 232

The next table illustrates the implementation of the original SHA-1 compression function, in this table the variables written in hexadecimal format.

Table 1. Implementation of the Original SHA-1 Hash Function

Variables	Variables in Hex
W 0	61626380
A	67452301
B	EFCDAB89
C	98BADCFE
D	10325476
E	C3D2E1F0
K1	5A827999
A <<<5	E8A4602C
B <<<30	7BF36AE2
F1 = E + ft(B,C,D)	5C7DDEEE
F2 = F1 + (A)«5	B6DDDCE0
F3 = F2 + W 0	18404060
New A = F3 + K 1	72C2B9F9

• 4.3.    Reducing the Complexity of SHA-1 in Step 1

In general, hash function algorithm starts with few calculation steps that can be done in advance. This pre-calculation suggests new value for public buffers which reduce the hash function complexity.

We can calculate the following operations in advance, because A, B, C, D, E, and Kt are known publically.

• •    Shift the value of (A) five positions to the left.

• •    Shift the value of (B) thirty positions to the left.

• •    Calculate the function of (B, C, and D).

• •    Calculate (T), which is equal to:

Т = ft (B.C.D) + E + A <<< 5 + Kt(6)

Next, we calculate the new values of A, B, C, D, and E as follows:

A1 = Т + Wj(7)

B1 = A

C1 = Shifted (B)

D1 = C(10)

E1 = D(11)

Т = 1160A679

Т + XQ = 72C2B9F9(13)

The following figure illustrates the reduced step 1 of SHA-1.

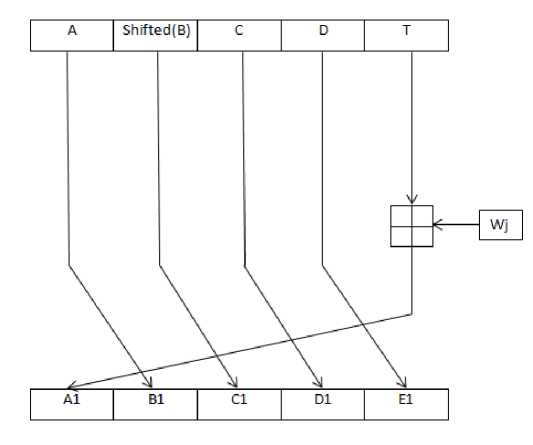
Fig.2. Reduced Single Step of SHA-1

If we compare the proposed solution in the first step with the original function of SHA-1, we can find that, the proposed solution reduces the number of operations from four addition mod32 operations to one addition mod32 operation only; accordingly, it reduces the compression function complexity and obtains the same results as shown in the following table:

Table 2. Implementation of the Proposed Function

Variables	Variables in Hex
X 0	61626380
A	67452301
B	EFCDAB89
C	98BADCFE
D	10325476
E	C3D2E1F0
K1	5A827999
A <<<5	E8A4602C
B <<<30	7BF36AE2
T = ft (B, C, D) + E + A<<<5 + K 1	1160A679
New A = T + W 0	72C2B9F9

• 4.4.    Reducing the Complexity of SHA-1 in Step 2

In this step, the values of A, B, C, D, and E as the following:

А1 = Т + Wj(14)

В1 = А(15)

С1 = Shifted (В)

D1 = С(17)

Е1 = D(18)

Based on that, we can calculate the preceding operations in advance.

Ft (В1, C1,D1) = Function of (А, shifted (В), С)(19)

X = Ft + Е1 = Ft + D + Kt(20)

The shifted (В1) = А <<< 30

Next, we calculate the new values of A, B, C, D, and E

Shift the value of (A) five positions to the left.

А2 = X + А1 <<< 5 + Wj(22)

В2 = А1(23)

C2 = В1 <<< 30

D2 = С1(25)

Е2 = D1(26)

The following figure illustrates the reduced step 2 of SHA-1.

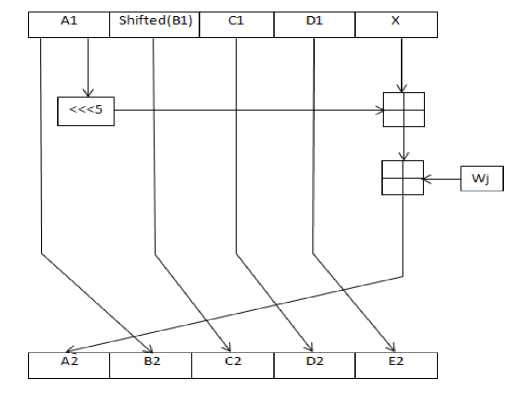
Fig.3. Reduced Second Step of SHA-1

If we compare the proposed solution in the second step with the original one, we can find that, the proposed solution reduces the number of operations from four addition mod32 to two addition mod32 only; accordingly, it reduces the compression function complexity also.

• 5.    MD5

• 5.1.    MD5 Algorithm Steps

In 1991 Ronald Rivest proposed a new MD5 algorithm as a replacement of MD4 hash function. This algorithm is the most widely used hash algorithm, particularly in Internet-standard message authentication. The algorithm can accept an input of an arbitrary length and produces an output of a 128-bit [6]. The researchers designed this algorithm for digital signature applications, where we can compress large files securely and encrypt the compressed copy with the private-key under a public-key cryptosystem such as RSA. Nowadays the researchers consider MD5 hashing insecure because they found algorithms that can generate MD5 collisions on low computation devices. Despite this, we can still apply MD5 as a checksum to confirm data integrity.

The MD5 hashing algorithm consists of four similar stages; each stage is divided into 16 steps compared to 20 steps in the SHA-1 algorithm.

As we mentioned earlier, the algorithm can accept an input of an arbitrary length and produces an output of a 128-bit.

To calculate the hash value of a given input, we can process the message input as the following five steps [6]:

Step 1: Append length of 64-bit value that represents the message length, if the message size is larger than 64bits, then find message size mode 2⁶⁴.

Step 2: Append padding bits to the message. Therefore, it can fit a size of 512-bit multiples.

Step 3: Initialize a 128-bit buffer to hold four 32-bit words.

Step 4: Processes the message in 512-bit blocks.

Step 5: The Output is the result of the message hash.

In the next section, we reduced the complexity that is occurred in step 4 (single step of MD5).

• 5.2.    MD5 Compression Function (single Step)

The researchers consider MD5 compression function as a heart of MD5 algorithm. This function divides the message into 512-bit blocks and processes each block separately.

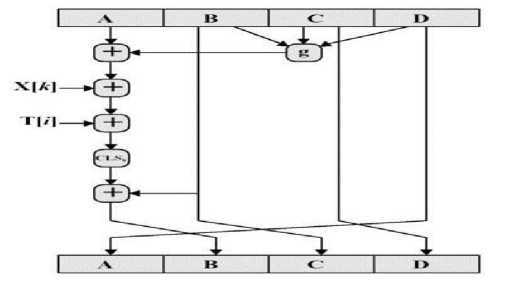
Fig.4. MD5 Operation (Single Step)

As illustrated in figure 4, the original MD5 compression function executes the following set of operations for each 32-bit message block to obtain the hash result:

F1 = A + Ft (B,C,D)

F2 = F1 + Xk(28)

F3 = F2 + Tj(29)

F4 = shift (F3)

New В = F4 + Old. В(31)

Where,

• A, B, C, D: 32-bit buffers used to hold intermediate and final results of the hash function.

Ft: one of the three logic functions: Majority, Choice, and XOR.

T i. : Binary integer part of the [Sin i x 2³²] (Radians).

Xk: Single word of message block.

+: addition modulo 232

The next table illustrates the implementation of the original MD5 compression function, in this table the variables written in hexadecimal format.

Table 3. Implementation of the original MD5 hash function

Variables	Variables in Hex
X 0	61626380
A	67452301
B	efcdab89
C	98badcfe
D	10325476
T 1	D76AA478
F1 = A + Ft (B, C, D)	FFFFFFFF
F2 = F1 + W 0	FFFFFFFFD76AA477
F3 = F2 + K 1	FFFFFFFFAED548EF
New B = F3 + Old B	5A722360

• 5.3.    Reducing the Complexity of MD5 in Step 1

As we mentioned earlier, hash function algorithm starts with few calculation steps that can be done in advance. This pre-calculation suggests new value for public buffers which reduce the hash function complexity.

We can calculate the following operations in advance, because A, B, C, D, and K t are known publically.

• •    Calculate the function of (B, C, and D).

• •    Calculate (T), which is equal to:

T = ft (B, C, D) + A + T[i].

Next, we calculate the new values of A, B, C, and D

А1 = D(32)

В1 = В + Rotate Left (Т + Х[/с])

С1 = В(34)

D1 = С(35)

The following figure illustrates the reduced step 1 of MD5.

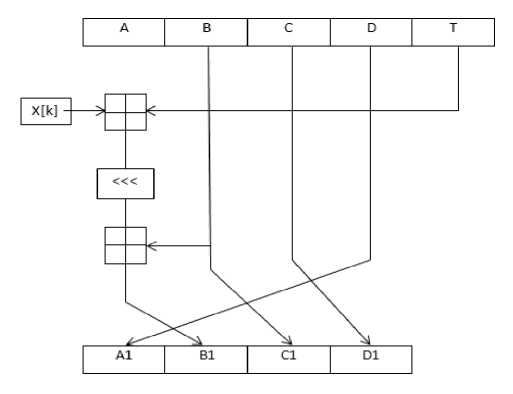
Fig.5. Reduced Single Step of MD5

If we compare the proposed solution in the first step with the original function of MD5, we can find that, the proposed solution reduces the number of operations from six addition mod32 operations to three addition mod32 operations only; accordingly, it reduces the compression function complexity and obtains the same results as shown in the following table:

Table 4. Implementation of the Proposed Function

Variables	Variables in Hex
W 0	61626380
A	67452301
B	efcdab89
C	98badcfe
D	10325476
K 1	D76AA478
T = Ft (B, C, D) + A + K 1	FFFFFFFFD76AA477
F1 = T + W 0	FFFFFFFFAED548EF
New B = F1 + Old B	5A722360

• 6.    Results

  • 6.1.    Reducing the complexity of SHA-1

In this section we compared the number of operations in the of the original SHA-1 function with the proposed function, and we found the complexity percentage is reduced by 75% on step 1, 50% on step 2, and 1.6% on the whole block(512-bit). Also, we compared the average time between the original SHA-1 function with the proposed function, we found the average time is reduced by 78% on step 1, 46% on step 2, and 8% on the whole block(512-bit).

The next table shows the results of first step, second step, and whole block reduced percentage compare with original function in SHA1.

Table 5. Complexity Comparison between the Original Function and Proposed Function in SHA-1

No of Operations	Original Function	Proposed Function	Reduced Percentage
Step 1(32bit)	4	1	75 %
Step 2(32bit)	4	2	50 %
Whole Block(512bit)	80 * 4 = 320	315	1.6 %

We implemented our proposed function and the original SHA-1 hash function using the java programming language to compare the average time between the two functions.

The following code illustrates the proposed function.

int[] w = new int[80];

int a = 1732584193;

int b = -271733879;

int c = -1732584194;

int d = 271733878;

int e = -1009589776;

int oldb = b;

int oldc = c;

int oldd = d;

int olde = e;

for(int j = 0; j < 80; j++) {

w[j] = (j < 16) ? blks[i + j] :

( rol(w[j-3] ^ w[j-8] ^ w[j-14] ^ w[j-16], 1) );

int t = rol(a, 5) + e + w[j] +

: (j < 40) ? 1859775393 + (b ^ c ^ d)

: -899497514 + (b ^ c ^ d) );

e = d;

d = c;

c = rol(b, 30);

b = a;

a = t;

} a = a + olda;

b = b + oldb;

c = c + oldc;

d = d + oldd;

e = e + olde;

}

The following table shows the implementation results.

Table 6. Time comparison between the Original Function and Proposed Function in SHA-1

Average Time \ nanosecond	Original Function	Proposed Function	Reduced Percentage
Step 1(32bit)	287	64	78 %
Step 2(32bit)	287	154	46 %
Whole Block(512bit)	11338	10415	8 %

• 6.2.    Reducing the Complexity of MD5

In this section we compared the number of operations of the original MD5 function with the proposed function, and we found the complexity percentage is reduced by 50% on step 1, and 0.8% on the whole block(512-bit). Also, we compared the average time between the original MD5 function with the proposed function, we found the average time is reduced by 47% on step 1, and 6% on the whole block (512-bit).

Also, the next table shows the results of step 1, and whole block reduced percentage compare with original function in MD5.

Table 7. Complexity Comparison between the Original Function and Proposed Function in MD5

No of Operations	Original Function	Proposed Function	Reduced Percentage
Step 1(32bit)	6	3	50 %
Whole Block(512bit)	64 * 6 = 384	(63*6)+3=381	0.8 %

Also, we implemented our proposed function and the original MD5 hash function by using java programing language to compare the average time between the two functions.

The following code illustrates the proposed function.

public static byte[] computeMD5(byte[] message)

int numBlocks = ((messageLenBytes + 8) >>> 6) + 1;

int totalLen = numBlocks << 6;

byte[] paddingBytes = new byte[totalLen - messageLenBytes];

paddingBytes[0] = (byte) 0x80;

long messageLenBits = (long) messageLenBytes << 3;

for (int i = 0; i < 8; i++)

messageLenBits >>>= 8;

} int a = INIT_A;

int b = INIT_B;

int c = INIT_C;

int d = INIT_D;

int[] buffer = new int[16];

for (int i = 0; i < numBlocks; i++)

{ int index = i << 6;

for (int j = 0; j < 64; j++, index++)

buffer[j >>> 2] = ((int) ((index < messageLenBytes) ? message[index]

: paddingBytes[index - messageLenBytes]) << 24)

| (buffer[j >>> 2] >>> 8);

int originalA = a;

int originalB = b;

int originalC = c;

int originalD = d;

int w= (b & c) | (~b & d);

int r = w + a;

int t= r+ 0xd76aa478;

for (int j = 0; j < 64; j++)

{ int div16 = j >>> 4;

int f = 0;

int bufferIndex = j;

if (j==0) { int ft = t + TABLE_T[j];

int temp = b + Integer.rotateLeft( ft,SHIFT_AMTS[(div16 << 2) | (j & 3)]); a = d;

• d    = c;

c = b;

b = temp;

} else { switch (div16)

{ case 0:

f = (b & c) | (~b & d);

break;

• case 1:

f = (b & d) | (c & ~d);

bufferIndex = (bufferIndex * 5 + 1) & 0x0F;

break;

• case 2:

f = b ^ c ^ d;

bufferIndex = (bufferIndex * 3 + 5) & 0x0F;

break;

• case 3:

f = c ^ (b | ~d);

bufferIndex = (bufferIndex * 7) & 0x0F;

break;

} int temp = b

• + Integer.rotateLeft(a + f + buffer[bufferIndex]

+ TABLE_T[j],

SHIFT_AMTS[(div16 << 2) | (j & 3)]);

a = d;

d = c;

c = b;

b = temp;

}

} a += originalA;

b += originalB;

c += originalC;

d += originalD;

} byte[] md5 = new byte[16];

int count = 0;

for (int i = 0; i < 4; i++)

{ int n = (i == 0) ? a : ((i == 1) ? b : ((i == 2) ? c : d));

for (int j = 0; j < 4; j++)

{ md5[count++] = (byte) n;

n >>>= 8;

}

} return md5;

}

The following table shows the implementation results.

Table 8. Time Comparison between the Original Function and Proposed Function in MD5

Average Time \ nanosecond	Original Function	Proposed Function	Reduced Percentage
Step 1(32bit)	588	278	47 %
Whole Block(512bit)	127491	120686	6 %

• 6.3. Impacts on Bitcoin Mining

• 7. Future Work

Bitcoin mining is the method of processing transactions on a Bitcoin network and securing them into the blockchain. The block is the collection of transactions that are processed and secured by the data miners. The miners secure the block by using a hash that is generated from the transactions in the block.

Every time the miners attempt to create a new block that contains current transactions and new hash before the others miners can do. To achieve that, they must solve a complex mathematical puzzle that is part of the bitcoin program and add the answer to the block. The puzzling problem is to find a number that, when combined with the data in the block and passed through a hash function, returns a result that is within a particular range.

The miners try to solve the puzzling problem many times to find the correct number, which consumes a high volume of energy. Therefore, the proposed solution reduces the hash function complexity, and the implementation time also. Accordingly, we can reduce energy consumption.

The results in this paper provide a strong foundation for future work in reducing hash functions complexity, one area of future work is reducing the complexity of remaining steps in hash function algorithms and obtaining the same results that are obtained by the original algorithm which will reduce the bitcoin mining power consumption.