Reduction of Blur in Image by Hybrid De-convolution using Point Spread Function

Published Online June 2016 in MECS DOI: 10.5815/ijigsp.2016.06.03

Images, including real life photographic and medical images are unfortunately captured blurred during their acquisition process due to various factors. Movement by the camera during image acquisition process, out of focus settings of the camera system and scattering of photons are some factors which cause blurring of images. This implies the necessity of image de-blurring in digital image processing. Image de-blurring which is considered as an inverse problem, involving de-convolution, finds extensive applications in many areas like digital photography, medical imaging, astronomy etc. Depending on the situation, image de-blurring can be blind image de-blurring, in which the true image and the blur kernel are unknown or non-blind image de-blurring, in which the blur kernel is known [1-3]. Through deblurring, images can be made sharp and more useful. In this paper a de-blurring method using Lucy Richardson algorithm is proposed, which uses the point spread function estimated from the blurred image. The algorithm is further tested on standard test images and medical images. In standard test images we consider blurring due to movement of camera and in medical images we consider blurring due to scattering of photons and movement of patient with respect to the imaging device.

Several enhancement methods, achieving effective deblurring, have been proposed in all fields of image processing including medical imaging, astronomical imaging, real life photography etc. Ref [4] and [5] presents a summary and analysis of many de-convolution algorithms. In [6] a two-step iterative shrinkage and thresholding algorithm has been proposed, exhibiting a faster convergence rate. A modified Lucy Richardson algorithm using DWT of the degraded image has been used in [7]. Kundur and Hatzinakos [8] proposed a ‘nonnegativity support constraints recursive inverse filtering (NAS-RIF) algorithm’ and it was extended to the 3D SPECT imaging restoration context in [9]. A blind deblurring approach to enhance image resolution without complete knowledge of the underlying point spread function in spiral CT images has been proposed in [10]. In [11] Lucy Richardson algorithm is modified using a projective motion blur model.

This paper proposes an image de-blurring method inspired by the idea of Lucy Richardson algorithm [12], [13]. A maximum likelihood estimate of the point spread function is first computed from the blurred image. A preprocessing stage is included to identify a suitable color space.

The subsequent sections of the paper are summarized as follows: Section 2 briefly reviews the basic theory behind image de-blurring. The proposed algorithm is given in section 3. Experimental results are illustrated in section 4 and section 5 concludes the paper.

• II.    Image de-blurring methodology

The objective of image de-blurring is to estimate the original image from the degraded version. For this a blurring model is assumed and de-blurring is performed using an inverse operation.

• A.    Image blurring model

An observed image with blur and noise as distortion factors can be modeled using a linear space invariant system. Fig. 1 describes such a model with the true image represented by t(x, y), the observed blurred image by b(x, y), the system transfer function by h(x, y) and the noise by n(x, y). Since the distortion factor is blurring, the system transfer function, also known as the point spread function, describes the degree of spread of a point light by the image acquisition system. Blurring is caused by the convolution of point spread function with the true image.

• B.    Blind de-convolution

As image de-blurring is an inverse problem, it uses some prior information about the true image and the degradation factor to obtain the true image. But practically in most cases the true image and the degradation factor are totally or partially unknown. So the problem becomes blind de-convolution. From the model given in Fig. 1 the observed blurred image can be written as given in (1).

b ( x , y ) = [ t ( x , y ) ∗ h ( x , y )] + n ( x , y )      (1)

‘*’ denotes two dimensional convolution.

The discrete model of (1) can be written as in (2).

b ( X ) = ∑ h ( X , s ) t ( s ) + n ( X ); X = ( x , y ) ∈ S (2) s ∈ S_h

S_t is the support of the image and S_h is the support of PSF. The problem of blind de-convolution becomes finding an estimate of the true image from an initial guess on the image and the point spread function.

• C.    Maximum likelihood estimate

Blind image de-convolution techniques differ in the assumptions made on the true image and the point spread function. One method is to compute the maximum likelihood estimate of the PSF parameters to perform blind de-convolution. Maximum likelihood estimation uses the fundamental Bayesian principle that regards all parameters as unknown stochastic quantities with assigned probability distributions. The probability of the observed blurred image is p(b) . The probability of the true image is p(t) . The likelihood function for the random process defined by (1) is denoted by p(b/t,h,n) . The maximum likelihood solution maximizes p(b/t,h,n) over t,h,n .

{ t_ML , h_ML , n_ML } = argmax p ( b / t , h , n )     (3)

t,h,n tML, hML, nML denote the maximum likelihood estimate of the true image t, PSF h and noise n.

• D.    Lucy Richardson algorithm

A potentially better approach for image de-blurring is Lucy-Richardson algorithm proposed by Richardson [13] and Lucy [12].

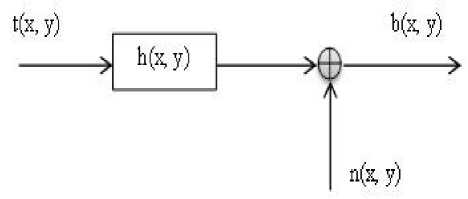
Fig.1. Image degradation model

It is an iterative method that maximizes the likelihood function, assuming Poisson statistics [12,13]. In [14] this is described as b -(h∗t) p(b/t)=Π(h∗t)e                (4)

x , y          b !

Equation (4) is maximized by minimizing the log likelihood function given in (5).

-log(p(b/t)) = ∫∫[(h∗t) -blog(h ∗t) + log(b!)]dxdy (5) x,y log(b!) is a constant relative to t. So we need to minimize the function given in (6).

F ( t ) = ∫∫ [( h ∗ t ) - b log( h ∗ t )] dxdy      (⁶)

• x , y

The function given in (6) is minimized by setting its derivative to zero. At convergence the iteration step is defined as in (7).

∧p+1   ∧p t =t [h∗ ∗b ]             (7)

∧ ^p

h∗t

_∧ p + 1

• t is the estimate of the true image at ( p+1) ^th iteration, ∧ ^p

t is the estimate of the true image at p ^th iteration and h^* represents the conjugate transpose of h . The method is effective for a known initial PSF.

• III.    Proposed method

In this paper we integrate the ideas of Lucy Richardson algorithm and blind de-convolution algorithm for developing an algorithm to de-blur gray scale and color images. The performance of the algorithm is tested using quantitative measures like peak signal to noise ratio, Tenengrad criterion and blur metric.

• A.    Proposed algorithm framework

As an initial step a suitable color space is identified for each image for carrying out de-blurring operation. This is done by analyzing the performance of edge detectors on the image in different color spaces. The acquired image is converted into different color spaces and edge is detected through a combined process of Gaussian smoothing, gradient filtering, non-maximum suppression and hysteresis thresholding [15]. The one which gives the best results in terms of detected edges is chosen as the color space for further processing. Since an iterative image deblurring algorithm is used, an initial estimate of the original image and the point spread function are to be provided as input. In our algorithm the blurred image itself acts as the initial guestimate value on the original image. Lucy Richardson algorithm can be effective only with a known PSF. But in the case of most real life images and medical images the PSF is unknown. Inspired by the idea proposed in [16] and [17], a maximum likelihood estimate of the PSF is obtained from the blurred image blindly (without the knowledge of true image and true point spread function) and this estimate acts as the initial guestimate value of the PSF for Lucy Richardson algorithm. The derivation of the algorithm given in this section is based on the paper from Shepp and Vardi [16]. The detailed algorithm is given below:

Step 1. Check whether the input image is in gray scale or color scale.

Step 2 . If the image is a gray scale image go to step 6, otherwise go to step 3.

Step 3 . If the image is in color scale, apply Canny edge detector to the image in three color scales: RGB, YCbCr and Lab.

Step 4 . Choose the color scale with the best edge map.

Step5 . Take the color channels individually. Individual color channels for the blurred image are represented as b i (x, y) , where i=1, 2, 3

Step 6 . Pre-filter each channel to reduce high frequency drops.

Step 7 . With an initial guess on PSF, find the maximum likelihood estimate of the PSF.

• a.    Set the maximum number of iterations to be executed as P .

• b.    Initialize the iteration number p=0

• c.    Make an initial guess on PSF

^(0)

hi (x, y) = ones(arbitrarysize)      (8)

Make an initial guess on image

^(0)

t i ( x , y ) = b i ( x , y ); i = 1,2,3        ⁽9)

• d.    Maximum likelihood estimate of PSF is computed iteratively

  Л p + 1             A p

  t .   ( x , y ) = t , ( x , y )

  
  

  ^ ^p

  h i ( x , y ) ^*

  
  

  b_i ( x , y )

  
  

Л P          A p hi (x, y)* ti(x, y) J (10)

AP+1             Ap hi (x, y) = hi (x, y)

_^ p^{bi ( x ,} _^ ^yp ⁾       * b i ( x , y ) ^*

h i ( x , y )* t i ( x , y )

• e.    Apply non negativity constraints on

A p + 1               A p + 1

t i  ( x , y ) and h i  ( x , y )

• f.   If p = P , stop iterations, otherwise p=p+1 and go to

step e.

^ ^P

• g.    New estimate of PSF is h i ( x , y )

Step 8 . With the new estimate of PSF as input, apply Lucy Richardson algorithm.

• B.    Performance measures used

To understand the performance of the proposed method in enhancing images through de-blurring, quantitative measures like peak signal to noise ratio (PSNR), Tenengrad criterion and blur metric are used. The definition of PSNR is as given in (11).

PSNR = 10*

log

Int _m ² _ax MSE

Int max denotes the maximum intensity in the image and MSE denotes the mean squared error. The higher the value of PSNR, the better is the quality of the image in terms of signal to noise ratio.

Tenengrad criterion [18] is a sharpness measure which is based on Sobel gradient operator. The higher the value of Tenengrad criterion, the better is the quality of the image in terms of sharpness.

The amount of difference in blur between the blurred image and the image de-blurred using our algorithm is evaluated using blur metric. This measure is based on the discrimination between different levels of blur perceptible on the same image [19]. The lower the value of blur metric, the better is the quality of the image.

Visual quality is used as the subjective measure for evaluating the performance of the proposed method. The difference between the blurred image and the de-blurred image can be easily determined by analyzing the images visually.

• IV.    Experimental Results

The proposed de-blurring algorithm is tested on blurred images and the performance is evaluated both qualitatively and quantitatively. Both standard test images and medical images are used for understanding the performance of the algorithm.

• A.    Qualitative analysis

Experiments are performed on 216 x 216 standard test images. The camera movement effect is introduced in the image using motion filters. Fig. 2 shows results of applying de-blurring techniques on peppers image in color scale and fig. 3 shows the results of applying deblurring techniques on Lena image in color scale. The deblurring techniques applied in fig. 3 are de-blurring using blind de-convolution (blind de-blurring) and de-blurring using proposed method. The visual quality of the image de-blurred using the proposed method is better as shown in fig. 3.

Cardiac single photon emission computed tomography (SPECT) images are a better diagnostic tool for assessing the functioning of the heart. With its widespread application and industry relevance, medical images from this domain are also opted in this paper for testing the performance of the proposed algorithm. The medical database consists of 45 images taken from 45 different patients in the age group from 40 to 65 years, including 12 patients with normal heart functioning and 33 patients with myocardial perfusion defects. 250 x 180 color images, each with 12 different heart slices and 110 x 400 gray images, each with 14 different heart slices are used for the experiments. Each heart slice shows the amount of blood in the left ventricle of the heart at an instant of time. The application of the proposed method on cardiac SPECT color and gray scale images gives the results as shown in Fig. 4 and Fig. 5 respectively. Fig. 5 shows the results of de-blurring the image using blind deconvolution (blind de-blurring), using Lucy-Richardson algorithm and using the proposed method.

• B.    Quantitative analysis

The proposed algorithm is evaluated in terms of blur metric, Tenengrad criterion and PSNR. The effectiveness of the proposed algorithm is also analyzed by comparing it with existing image de-blurring algorithms. Table 1 illustrates the de-blurring results of proposed method and other de-blurring methods on the standard peppers image in terms of blur metric, Tenengrad criterion and PSNR. From Table 1 it is clear that the proposed method performs better than blind de-blurring method, in terms of blur metric, Tenengrad criterion and PSNR. A comparison between the de-blurring results of the proposed method and other classical de-blurring methods on cardiac SPECT images is presented in Table 2. The use of the proposed method yields a lower blur as indicated by the blur metric, better sharpness as indicated by the value of Tenengrad criterion and lower noise as indicated by the value of PSNR. It has to be stressed that if Lucy Richardson algorithm is applied directly on SPECT images, a considerable amount of noise is added as indicated by the lower PSNR value. The effect is indicated by the images in Fig. 5. Fig. 6 presents a comparison between the proposed method and blind deconvolution method in de-blurring a blurred image. It shows the results of de-blurring 10 sample images from the cardiac SPECT database. The plots emphasize the efficiency of proposed method in reducing blur. The plots in Fig. 7 substantiate the ability of the proposed method in improving signal to noise ratio as compared to blind de-convolution method.

• C.    Convergence of the algorithm

Lucy-Richardson (LR) algorithm converges well for a known PSF scenario if the initial PSF is chosen correctly. In this paper we consider an unknown PSF scenario. So in order to ensure the convergence of the algorithm initial PSF for Lucy-Richardson algorithm needs to be selected carefully. Blind de-convolution is an accepted method for estimating PSF in an unknown PSF scenario. Initial PSF for the LR algorithm is estimated by using iterative blind de-convolution algorithm given in (10). More iterations improve fitting but with an addition of noise. A compromise value of number of iterations needs to be chosen which gives a better fitting at a reasonable PSNR value. The experiments show that the convergence of LR algorithm is good when the PSF estimated by (10) acts as the initial PSF. With a random initial PSF the PSNR value is less as shown in Table 3.

Fig.2. Application of de-blurring algorithms on peppers image

Slurred image

Deblurred image using blind deconvolution Deblurred image using proposed method

Fig.3. Application of de-blurring algorithms on Lena image

Blurred image                                     De-blurred image using proposed image

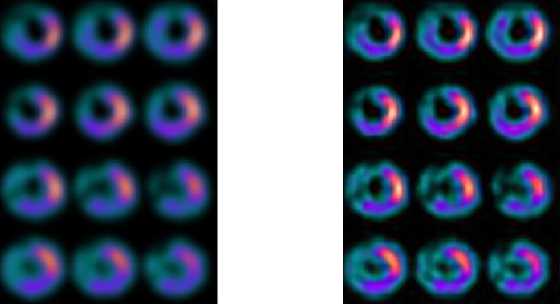
Fig.4. Application of proposed method on cardiac SPECT color image

Blurred image

De-blurred image using blind deconvolution

De-blurred image using Lucy-Richardson algorithm

De-blurred image using proposed method

Fig.5. Application of de-blurring algorithms on cardiac SPECT gray scale images

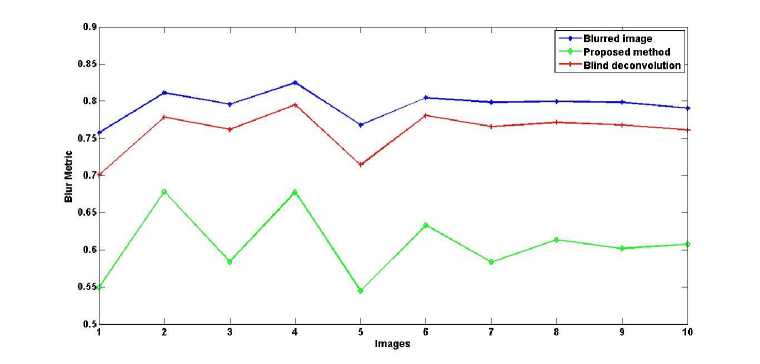
Fig.6. Comparing blind de-convolution method and proposed method in terms of blur

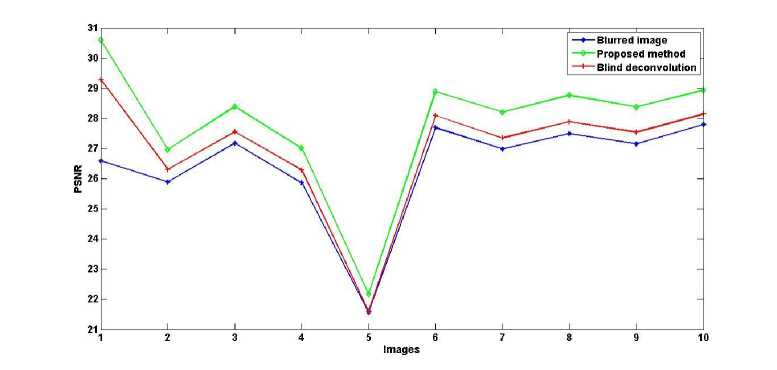
Fig.7. Comparing blind de-convolution method and proposed method in terms of PSNR

Table 1. Comparison results of applying de-blurring algorithms on peppers image

Method	Blur Metric	Tenengrad Criterion	PSNR
Blurred image	0.7224	5.29*103	22.75
Blind deblurring	0.6427	8.8*103	24.14
Proposed Method	0.6058	9.63*103	24.27

Table 2. Comparison results of applying de-blurring algorithms on cardiac SPECT image

Method	Blur Metric	Tenengrad Criterion	PSNR
Blurred image	0.8113	1.36*10 3	25.89
Blind deblurring	0.7785	1.8*10 3	26.31
Proposed Method	0.6778	2.82*10 3	26.96

Table 3. Effect of estimating initial PSF on PSNR value

PSNR value with estimated initial PSF	PSNR value with a random initial PSF
25.3378	17.4353

• V.    Conclusion

In this paper, a hybrid de-blurring method based on Lucy Richardson algorithm and blind de-convolution algorithm is proposed. The proposed method differs from the existing de-blurring techniques in a manner that it extracts an estimate of the point spread function from the blurred image itself and then this estimated point spread function is used in Lucy Richardson algorithm. A preprocessing stage is also used to identify a better color space for further processing. This makes the algorithm suitable for de-blurring gray scale and color images. Simulations are conducted using standard test images and real SPECT medical images. The performance of the algorithm is tested in terms of blur metric, Tenengrad criterion, PSNR and on the basis of the visual quality of the image. A comparative study between different deblurring algorithms proves that the proposed method which uses a combined approach of Lucy Richardson and blind de-convolution algorithms yields the better output in terms of reduction in blur with high PSNR value.