Региональные банки на пиках инфляции

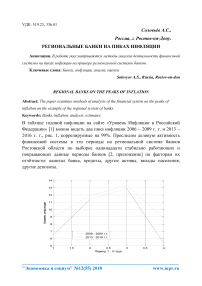
В таблице годовой инфляции на сайте «Уровень Инфляции в Российской Федерации» [1] можно видеть два пика инфляции 2006 – 2009 г. г. и 2013 – 2016 г. г., рис. 1, коррелируемые на 99%. Проследим деловую активность финансовой системы в эти периоды на региональной системе банков Ростовской области по выборке одиннадцати стабильно работающих и покрывающих данные периоды банков [2, приложение] по факторам их отчётности: капитал банка, кредиты, другие активы, вклады населения, другие депозиты.

Рис. 1. Инфляция в периоды 2006 – 2009 и 2013 – 2016 г. г.

В данных факторах отражается не только поведение самих банков, но и активность населения и бизнеса. Исходная информация представлена посредством активов и депозитов, но легко приводится к приведённым выше факторам. Поскольку на деятельности самой финансовой системы влияют не только действия самой системы, населения и бизнеса, но действие такого массового фактора, как инфляция, и этот фактор изменяется во времени, то при анализе поведения на циклах инфляции данный массовый фактор следует исключить. Для этого воспользуемся тем, что годовые отчётные данные приводятся вместе с годовым уровнем инфляции.

Будем считать состоянием системы гипотетический объект, совпадающий с её средним состоянием. Данный объект также находится под воздействием тех же массовых сил. Если принять состояние системы за измерительный эталон и пофакторно каждый объект системы разделить на него, то, во-первых, избавимся от действия инфляции на систему, а во-вторых, все факторы системы приобретут одинаковый вес в анализе данных. Приходим к представлению состояний финансовой системы в системе декартовых координат R ⁵ и в безразмерном виде в пространственно– временной структуре. Для примера приведём расчётную матрицу для состояния системы в 2006 году

Л06 =

0.1494 0.1967

/ 0.4519

0.3128 0.4459

0.5010

0.0347

0.1752

0.6316

0.2591

0.3518

0.1939

0.3689

0.7619

0.0138

0.0484

0.1050

0.1547

0.4282

0.0751

0.2581

0.9720

0.0438

0.0857

0.2206

0.3215

0.3106

0.4164

1.5074

0.0208

0.0770

0.0000

0.0571

0.4076

0.1344 0.0653

0 0.0912 0.2380 0.0008

0.0449 0.0919

0.0789 0

\

\ 7.6325 8.6094 7.9326 7.9429 10.0210 /

0.6189 0.2377 0.4078 0.0597 0.4333 / и вектор состояния системы

006 =[263362 1.214015 668064 582581 334158].

Каждому объекту системы отвечает вектор-строка расчётной матрицы. Если перейти в пространство L ², то можно поставить каждому объекту в соответствие количественную интегральную характеристику – его модуль, и характеристику его качества – как пространственное расположение единичного вектора относительно других объектов в евклидовом пространстве E ⁵ с мерой, заданной скалярным произведением.

B 06 =

1.	0.2498	0.3289	0.5230	0.7456	0	0.5980
2.	0.5890	0.4809	0.3364	0.5427	0.1188	0.7673
3.	0.2473	0.3760	0.4797	0.7440	0.1175	2.0262
4.	0.5665	0.2257	0.7160	0.3395	0.0136	0.0612
5.	0.8141	0.2250	0.3984	0.3577	0	0.2152
6.	0.9306	0.1548	0.3250	0.0000	0.0661	0.6787
7.	0.5707	0.3408	0.7081	0.1257	0.2024	0.4540
8.	0.4635	0.5642	0.4093	0.5371	0.1039	0.7589
9.	0.7573	0.2932	0.5249	0.2549	0	0.2561
10.	0.4029	0.4545	0.4188	0.4193	0.5290	18.9424
11.	0.6931	0.2663	0.4568	0.0669	0.4853	0.8929

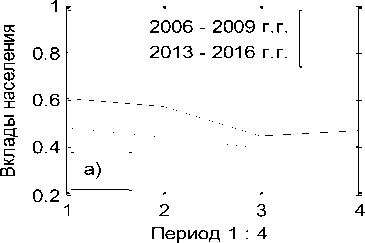
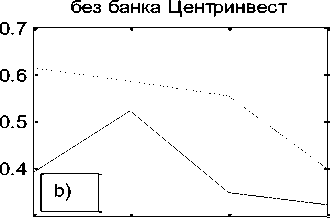
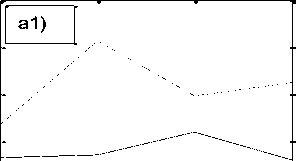
Первый столбец матрицы B06 указывает номер объекта. В столбцах 2 -6 размещены компоненты состояния объектов. В седьмом столбце приведены их модули. Из матрицы B06 видим, что объект под номером 10 (банк «Центр-инвест», [3]) имеет превосходящий модуль над всеми другими объектами системы в каждом временном интервале, даже в их сумме. Именно он и формирует измерительный эталон системы в каждой точке наблюдения, смысл которого как раз и заключается в независимости факторов. Компоненты десятого объекта близки к компонентам единичного направляющего вектора эталона системы, которые равны 0.4472. Поэтому целесообразно рассмотреть параллельно, опираясь на исходные данные, два состояния финансовой системы: a) - финансовой системы в целом, и b) - данной системы без десятого объекта (без банка Центр-инвест). Графики количественной и качественной динамики системы приведены на рис. 2.

Если рассматривать систему в целом, то из a1) следует, что на первом пике инфляции (штриховая линия) система осуществляет интенсивную линейно возрастающую структурную перестройку. Однако, на графике количественной оценки a) наблюдаем постоянное снижение её количественного показателя. Из второго графика (сплошная линия) видим, что во второй пик инфляции система вошла с выученным уроком на первом пике. При ускорении инфляции снижается уровень количественной оценки, что побуждает к структурной перестройки состояния системы. Последнее не только замедляет падение количественной оценки деятельности системы, но приводит к её росту и дальнейшей стабилизации.

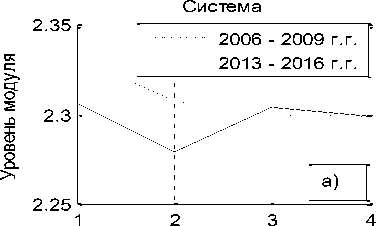
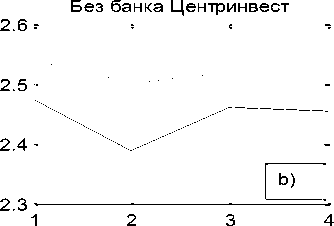
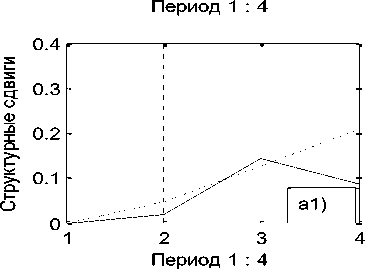
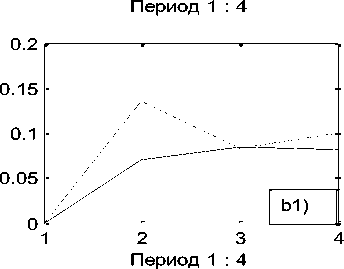
Рис. 2. Динамика количества и качества системы. Штриховой линией отмечена в периоде 2006 – 2009 г.г., сплошной – в периоде 2013 – 2016 г.г. Фиг. a), b) – динамика количественного роста, фиг. a1), b1) - динамика изменения качества.

Если обратить внимание на показатели малых банков (рис. b), b1)), то с вхождением в первый пик инфляции, 2006 – 2009 г.г., и падение количественной оценки деятельности вызвало бурную структурную перестройку, которая привела к росту количественного показателя. Однако, снижение интенсивности качественной перестройки снова привело к падению количественного показателя, что снова побудило к структурной перестройке в системе малых банков. Из данных графиков видим значительное влияние на стабилизацию деятельности системы крупнейшего банка данной региональной системы, банка Центр-инвест.

Структурная перестройка системы осуществляется перестройкой отношения между факторами системы. В данном случае между капиталом, активами и депозитами, и их составляющими. Каждый рассматриваемый период состоит из четырех лет – из четырёх точек наблюдения факторов-индикаторов: капитала, кредитов, других активов, вкладов населения и других депозитов, т.е. наблюдений системы в пространстве E ⁵. Поскольку индикаторы являются относительными величинами и характеризуются выпуклыми функциями, то по их отношениям можно судить о поведении наблюдаемой как в пространстве L , так и в пространстве L ². Поэтому выпишем эволюцию системы в каждом периоде в данных относительных показателях. Так, в периоде 2006 – 2009 годы она описывается матрицей 1.0e+06 *

0.2634  1.2140  0.6681  0.5826  0.3342

0.4233  2.0776  1.1022  0.9203  1.3067

0.5185  3.4577  1.9422  1.3701  1.3679

0.7595  3.6163  5.4765  1.5392  2.4621

Здесь каждая строка отвечает состоянию системы, наблюдаемом в соответствующем году данного инфляционного периода. Если теперь все

элементы  каждой  строки  разделить	на	максимальный	элемент
соответствующей строки
0.2169  1.0000  0.5503	0.4799	0.2753
0.2037  1.0000  0.5305	0.4430	0.6290
0.1500  1.0000  0.5617	0.3963	0.3956

0.1387  0.6603  1.0000  0.2811  0.4496

то в пространстве L пропорции элементов строк будут характеризовать качество состояния системы в соответствующем году рассматриваемого периода наблюдения, а элементы столбцов оценят изменения факторов в происходящих качественных преобразованиях системы в целом. Динамика оценок факторов при качественных преобразованиях системы в каждом периоде наблюдения инфляции представлены на рис. 3 – 5.

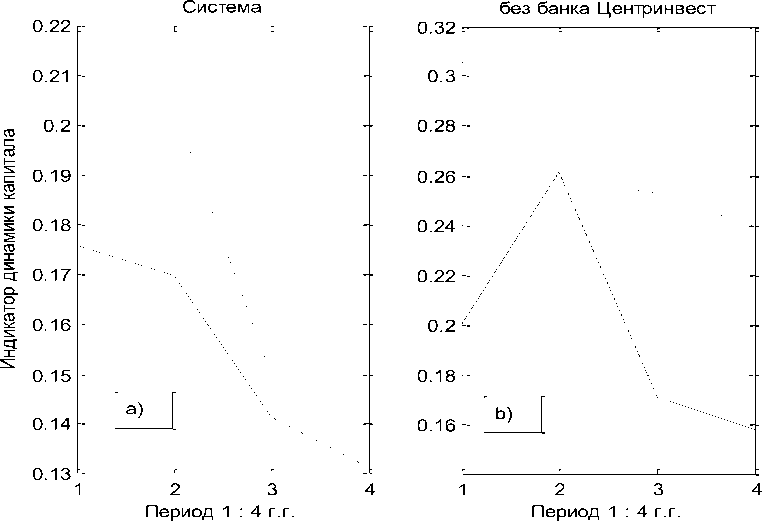
Рис. 3. Динамика капитала

Другие активы                   Кредиты

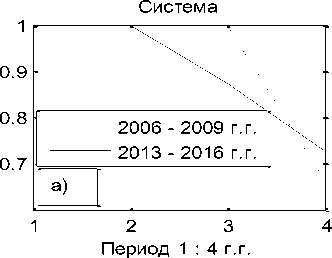
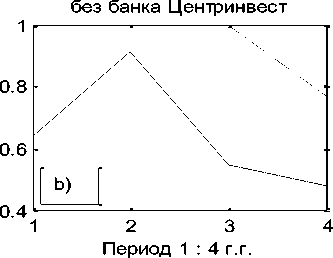
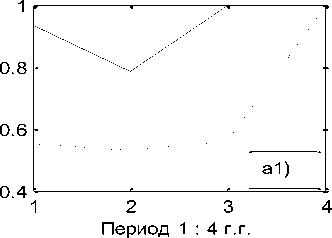
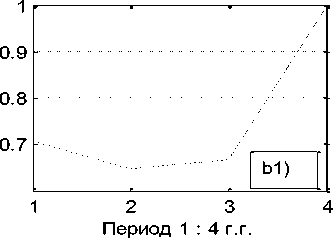
Рис. 4. Динамика активов.

Система

0.8

0.6

0.4

0.2

Период 1 : 4

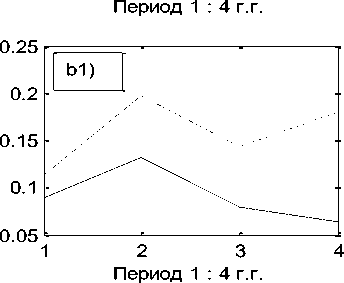
Рис. 5 Динамика пассивов.

Из графиков видно, что вход в инфляционный пик система воспринимает как неожиданную ударную волну, что может свидетельствовать о несовершенстве прогнозов ожидания.