Регрессионная модель энергоемкости процесса электродиализа воды

Кияшко Елена Александровна; Kiyashko Elena Alexandrovna

Регрессионная модель энергоемкости процесса электродиализа воды

Автор: Кияшко Елена Александровна

Журнал: Вестник аграрной науки Дона @don-agrarian-science

Рубрика: Механизация и электрификация животноводства, растениеводства

Статья в выпуске: 4 (16), 2011 года.

Бесплатный доступ

С помощью уравнений регрессии исследована трехмерная модель электродиализа водопроводной воды. Установлено, что из трех выбранных факторов на энергоемкость процесса электродиализа воды влияют напряжение на электродах и расстояние между электродами.

Вода, электродиализ, уравнение регрессии, напряжение, расстояние между электродами

Короткий адрес: https://sciup.org/140204120

IDR: 140204120 | УДК: 631.172:633.1

Regression model of power consumption of water electrodialysis process

Three-dimensional model of the tap water electrodialysis is investigated by means of the regression equations. It is established from three chosen factors the tension on electrodes and distance between electrodes influence on the power consumption of the electrodialysis process.

Текст научной статьи Регрессионная модель энергоемкости процесса электродиализа воды

До настоящего времени исследование модели, определяющей зависимость энергоемкости процесса электродиализа водопроводной воды, производилось от двух факторов: q = f Q;U ) или q = f Q;L ) , где Q – производительность установки, л/ч;

U – напряжение на электродах, В.

L – расстояние между электродами, мм.

В настоящем исследовании рассматривается трехфакторная модель электродиализа воды q = f ( Q;L;U ) .

Для исследования трехфакторной модели электродиализа применялся математический аппарат планирования научного эксперимента [1, 2]. К исследованию были

приняты следующие факторы: X j = Q ,

X2 = L, X3 = U.

В качестве отклика был принят удельный расход электроэнергии, который определяется по формуле

q=Q'

где P – мощность, потребляемая установкой, кВт;

q – удельный расход электроэнергии

(энергоемкость), кВт ч/л.

Для описания возможной связи отклика с принятыми факторами используем линейное уравнение регрессии первого по-

рядка:

Y = bg + by • X^ + b2 • X2 + b • X2,

где Xi, X2, X3 - принятые к исследо ванию факторы;

bo, bi, b2, Ьз - коэффициенты ре грессии.

Условия эксперимента представлены в таблице 1.

В качестве плана эксперимента выбираем полный факторный эксперимент 3

(ПФЭ) типа 2 . Кодированная матрица планирования 2 , результаты эксперимен та, а также фиктивная переменная Xо = 1 представлены в таблице 2.

Условия проведения эксперимента

Таблица 1

Обозначение факторов	X 1 = Q, л/ч	X 2 = L, мм	X 3 = U , В
Основной уровень	85,0	255,0	150,0
Интервал варьирования	10,0	120,0	50,0
Верхний уровень (+1)	95,0	375,0	200,0
Нижний уровень (-1)	75,0	135,0	100,0

Таблица 2

№	X₀	X 1	X 2	X₃	Y
1	+	-	-	-	)? • 10 4
2	+	+	-	-	16 ^ 10 4
3	+	-	+	-	61 • 10 4
4	+	+	+	-	51 • 10 4
5	+	-	-	+	33 ^ 10^-4
6	+	+	-	+	27 ^ 10 ¹
7	+	-	+	+	139 ^ 10 ¹
8	+	+	+	+	108 ^ 10^-4

Кодированная матрица и результаты эксперимента

Для расчета коэффициентов регрессии составляем таблицу 3.

Коэффициенты регрессии вычисляем по формуле

bj =

2 Xji • Yi V i=i

/N ,

В результате решения этой матрицы

получили уравнение регрессии:

Y = 56,5 • 10-4 - 6 • 10-4X + 33,25 • 10-4X + 32,75 • 10-4X -

- 4,25 • 10-4 XX - 3,4 • 10-4 XX +13,5 • 10-4 XX - 2 • 10-4 XXX.

Кодированная матрица и результаты эксперимента

Таблица 3

№	^X0	X 1	X 2	^X3	^X 1 • X 2	X 1 - X 3	^X2 ' ^X3	X 1 • X 2 • X 3	Y
1	+	-	-	-	+	+	+	-	17 ^ 10 4
2	+	+	-	-	-	-	+	+	16 ^ 10^-4
3	+	-	+	-	-	+	-	+	61 • 10 4
4	+	+	+	-	+	-	-	-	51 • 10 4
5	+	-	-	+	+	-	-	+	33 ^ 10^-4
6	+	+	-	+	-	+	-	-	27 ^ 10 ¹
7	+	-	+	+	-	-	+	-	139 ^ 10^-4
8	+	+	+	+	+	+	+	+	108 ^ 10^-4

Для определения дисперсии воспро- лены три параллельных опыта в центре изводимости были дополнительно постав- плана и получены значения:

Y10 = 49 • 10- 4; Y20 = 40 • 10- 4; Y = 34 • 10- 4.

Откуда

_ 2 Yi 0 123 ,

Yo = ^=1— =---= 41 • 10 4,

03 3

2(Y0 - Y0)

c 2 _ i = 1 __________

Sy = 7

114•10"8

= 57•10-8,

Sy = 7,55 • 10 — 4.

Дисперсия коэффициентов регрессии равна:

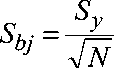
7,55 • 10 "4

2,83

= 2,66 • 10- 4.

Оценим значимость коэффициентов регрессии по критерию Стьюдента по фор-

муле

tj =

b j

S • b j

В соответствии с табулированным значением критерия Стьюдента для уровня значимости a = 0,05 и числа степеней свободы f = m = 3 — 1 = 2 , І кр = 4,3 получено новое уравнение регрессии:

Y = 56,5 • 10-4 + 33,25 • 10—4 X + 32,75 • 10—4 X +13,5 • 10 4 XX. (9)

Проверяем адекватность полученного уравнения по критерию Фишера:

S (Y-YJ2

F p = S ocm.^/Sу , S ocm. = ,_M 77 , ⁽¹⁰⁾

(N l)

где / = 4 - число значимых коэффициентов в уравнении регрессии (9);

S² – остаточная дисперсия.

ост.

Для расчета остаточной дисперсии составляем таблицу 4.

Таблица 4

№	^Yi	Л Y i	Y i — Y ' l	( л) ² Y i — Y i k 7
1	17 ^ 10 " ⁴	4 - 10 " ⁴	1370^-4	169 ^ 10^-8
2	1640 " ⁴	4 ^ 10 "4	12 ^ 10^-4	144 ^ 10^-8
3	6Н0 " ⁴	43,5 •Ю^-4	17,5 •Ю^-4	306 ^ 10^-8
4	51 ^ 10 " ⁴	43,5 •Ю^-4	7,5 •Ю^-4	56 ^ 10^-8
5	33 • IO^-4	42,5 ^ 10 " ⁴	-9,5 •Ю^-4	90 ^ 10^-8
6	27 ^ 10 " ⁴	42,5 ^ 10^-4	-15,5 ^ 10^-4	240 ^ 10^-8
7	139 ^ 10 ¹	136 ^ 10^-4	3 ^ 10^-4	9 ^ 10^-8
8	108 ^ 10^-4	136 ^ 10^-4	-28 •Ю^-4	784 ^ 10^-8

Определяем остаточную дисперсию

² ост.

1798 • 10— 8

= 449,5 • 10—8,

тогда F p =

449,5 • 10—8

57•10—8

= 7,88.

Табулированное значение критерия

Фишера для a = 0,05, f1 = 4,0,

f2 = 2,0 равно FKp = 19,3.

Если FKn > Fn, то полученное урав-кр . p нение (9) адекватно описывает эксперимент.

Для практического использования полученного уравнения удобно перевести его в натуральный масштаб, тогда оно примет следующий вид:

Y = 464 • 10—4 + 33,25 • 10—4 L + 32,75 • 10—4 U +13,5 • 10—4 LU. (11)

Выводы

1. В результате проведенных исследований установлено, что из трех выбранных факторов на энергоемкость процесса электродиализа воды влияют напряжение на электродах и расстояние между электродами.
2. Полученная регрессионная модель адекватно описывает результаты эксперимента.

Список литературы Регрессионная модель энергоемкости процесса электродиализа воды

Бирюков, В.В. Практическое руководство по применению математических методов планирования эксперимента для поиска оптимальных условий в многофакторных процессах/В.В. Бирюков. -Рига: Зинатне, 1969. -186 с.
Сычевская, И.Д. Обзорная информация ТС-4 «Аналитические приборы и приборы для научных исследований: планирование научного эксперимента/И.Д. Сычевская. -Москва, 1976. -81 с.