Регрессионно-дифференциальная модель динамики горной промышленности Пермского края

В последнее время в связи с неустойчивостью экономики, как в стране, так и в мире, все большую значимость начинает приобретать социальная статистика. Она способна обеспечить органы управления объективной информацией о развитии социальных процессов в обществе. Такие статистические данные необходимы для выявления тенденций развития той или иной сферы деятельности людей. Кроме всего прочего социальная статистика применяется в моделировании социальноэкономических систем, на основе анализа которых проводятся оценки характеристик сложных систем, для принятия решений в различных сферах деятельности людей.

Для построения моделей социально-экономических систем применяются различные математические методы, например: временные ряды, авторегрессионные модели разных порядков, линейные многофакторные модели и регрессионно-дифференциальная модель [0] .

Объектом моделирования выбрана отрасль горнодобывающей промышленности Пермского Края, поскольку здесь добыча полезных ископаемых занимает одно из значимых мест в развитии всего региона. Исследования проводились на основании статических данных за 8 лет [4] .

Динамика горной промышленности оценивалась объему отгруженных товаров собственного производства (табл. 1), произведенных из полезных ископаемых. В качестве исходных данных – факторов, которые влияют на уровень добычи полезных ископаемых, могут выступать затраты связанные с проведением вскрышных работ, отвалообразованием, горнотехнической рекультивацией и т.д. Учитывая, что по этим данным нет информации в открытых источниках выбраны показатели имеющие отношение как к этим работам, так и к добычи полезных ископаемых в целом (табл. 2).

Таблица 1. Годовой ряд критерия

Критерий \ номер года в ряду	1	2	3	4	5	6	7	8
Объем отгруженных товаров собственного производства (работ, услуг)	138	121,1	110	114,1	95,4	124,2	134,4	115,1

Таблица 2. Факторы

Фактор \ номер года в ряду	1	2	3	4	5	6	7	8
Среднегодовая численность работников организаций находящихся в государственной собственности	0,2	0,4	0,2	0,4	0,3	0,3	0,3	0,3
Среднегодовая численность работников организаций, находящихся в частной собственности	55,8	62,8	67,4	68,8	69,7	69,7	73,8	72
Среднегодовая численность занятых в экономики	18,3	17,9	18	18,6	17	16,8	17,2	18,1
Число действующих предприятий	145	167	173	185	168	235	276	302
Валовая добавленная стоимость	15,7	15,9	14	12,1	13,3	13,5	15,6	18,1
Рентабельность проданных товаров	59,9	65,2	65,7	40,8	61	44,4	32,3	37,8
Индекс цен производителей промышленной продукции	113,4	110,4	125,1	93	113,9	116,7	112	105,1

Значения годовых рядов критерия и факторов перед использованием нормированы для исключения влияния размерности.

Линейная многофакторная модель (ЛММ) для нашего исследуемого объекта имеет следующий вид:

y ( x ( t ) ) = a 0 + ^ a i x i ( t ) ,

i где коэффициенты влияния одиночных факторов ai получены минимизацией квадратичного отклонения модельных данных от статистических.

ЛММ хорошо приближает исходные данные, квадратичная погрешность аппроксимаций составляет 0,0003688. В качестве необходимого условия возможности прогнозирования принято, что модель должна быть способна к постпрогнозу хотя бы на один последний год. Однако при уменьшении количества «известных» лет на один - два года для определения допустимого горизонта прогнозирования погрешность прогноза увеличилась до 1,55 и 165,32 соответственно. Следовательно, линейная модель не подходит для прогнозирования динамики объекта (рис. 1).

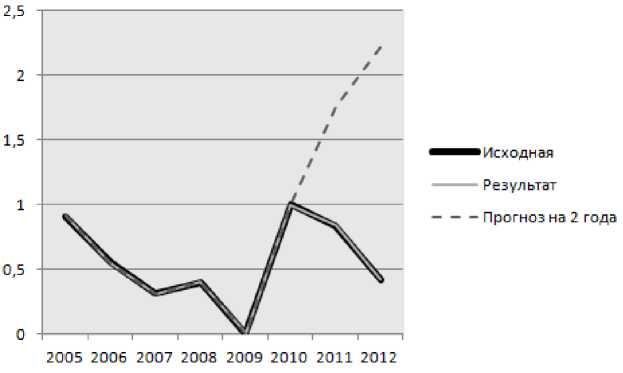
Рис. 1. Построение модели с использованием ЛММ

Поэтому было принято решение использовать регрессионно-дифференциальную модель (РДМ) вида [ Ошибка! Источник ссылки не найден. ]:

^{dyt )} + g . dy l t ) = a + b . y ( t ) + m c . .x ( t ) + £ jr ^d „ -x . ( t ) • x . ( t ) ⁺ ^T ^f •[ x . ( t ) ] ²,          ⁽¹⁾

^{dt              dt}                         = 1                 = 1 j = 1                           = 1

где g – коэффициенты влияния младших производных, a – константа, описывающая влияние одной n -й производной реакции при построении тренда, b – коэффициент «обратной связи», описывающий влияние значения реакции на ее же n -ю производную, c – коэффициенты влияния факторов, d : i * j — коэффициенты взаимного влияния факторов, f = d_it - коэффициенты влияния квадратов факторов, т — запаздывание в обратной связи, у - запаздывание воздействия i -го фактора. РДМ до- dy ( 0 )     ,    d ² y ( 0 )     .          d ⁽ n ^{- 1 )} y ( 0 )      ( n - 1 )

полняется начальными условиями —^- = y ₀, --- ^ = y ₀, .. , --- '  = y ( ) .

dt              dt2                     dt(n -1)

Неизвестными в данном случае являются все начальные условия, а также начальные условия y 'o... y ^{( n - 1)} , a , b , C i , d ij , f i , т о , т i . Их поиск производится минимизацией квадратичного отклонения расчетного значения y ( t_k ) от известных в отсчетах значений критерия y _Hcх ( t_k ) :

K-19

• ⁵ = Ё ( y ( t k )^- y исх ( t k ) ) , k = 0

  
  

то есть решением задачи минимизации

{y '0, a, b, c., dj, fi ,т0,т }: 5 (y '0, a, b, c., d ., f ,т0,т,)^ min.(3)

При построении модели первого порядка погрешность аппроксимации S составила 4,63. Минимальную погрешность S = 0,063 приближения к известным данным осуществляет модель второго порядка (рис. 2), поэтому дальнейшее исследование мы будем проводить с ней.

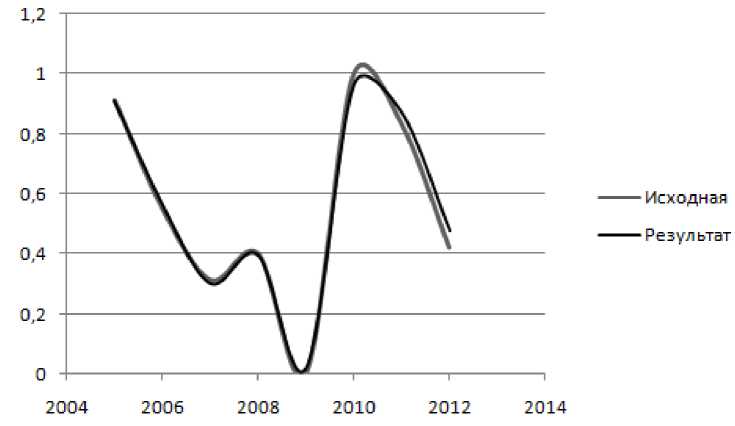
Рис. 2. РДМ 2-го порядка

Полным перебором был произведен подбор интерполяции факторов, позволяющей найти значения между узлами ряда. Например, стоимость основных фондов предприятия в 2006 г.» может означать, как стоимость на 1 января, так и на 31 декабря. В первом случае необходимо использовать ступенчатую интерполяцию, «распространяя» значение в начале года на весь год («левая» интерполяция), во втором - «правую» интерполяцию. Общий перечень возможных видов интерполяции:

• -    «левый» (указано значение в начале года, действующее до конца года; далее обозначен «0»);

• -    «правый» (указано значение в конце года, действовавшее весь год; далее обозначен «1»);

• -    линейный (указано значение в начале года, которое линейно изменяется до конца года; далее обозначен «Л»);

• -    фактор выключен (далее обозначен «Х») [ Ошибка! Источник ссылки не найден. ].

Получены следующее результаты:

• -    факторы 1 и 6 можно не использовать («Х»);

• -    у 2, 4 и 5-го факторов значение, указанное в конце года, остается постоянным весь год («0»);

• -    значение 3-го и 7-го факторов указанное в начале года линейно изменяется до конца года («Л»).

На наш взгляд, это вполне логично, т. к. объем отгруженных товаров действительно зависит от числа действующих предприятий, валовой добавленной стоимости и индекса цен производителей. Результат поведения модели после исключения 1 и 6 факторов отображен на рис. 3. При таком положении движков погрешность аппроксимации составляет 0,0108, т. е. подобранная интерполяция движков уменьшила погрешность аппроксимации на 5,22%.

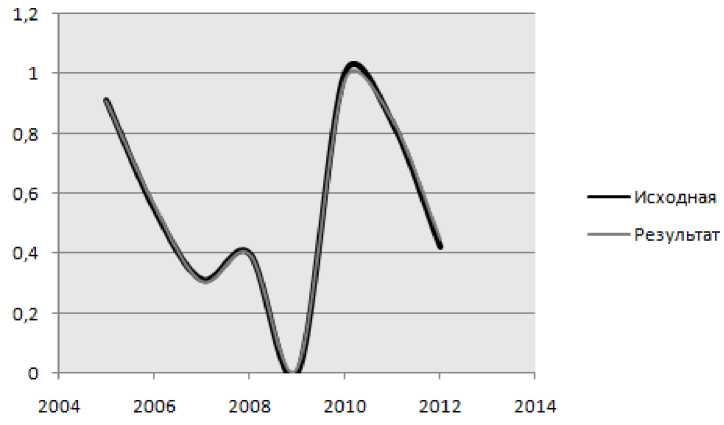
Рис. 3. Модель 2-го порядкас подобранным видом интерполяции

Далее для построения прогноза определим допустимый горизонт прогнозирования. Будем по известным данным уменьшать количество лет до тех пор, пока погрешность прогнозирования не увеличится более чем на 10%. В результате получено, что при уменьшении количества известных лет на 1, 2, 3 года погрешность прогноза увеличилась, соответственно, на 0,26, 5,6% и на 11,65% соответственно. Значит, горизонт возможного прогнозирования составляет 2-3 года.

Динамика факторов за последние 4 года в каждом ряду позволяет сделать вывод, что все они имеют примерно линейный характер изменения. Для построения положительных и отрицательных вариантов прогноза были выделены управляемые и неуправляемые факторы:

• -    факторы, которыми лицо, принимающее решение (ЛПР), может управлять это 5-й и 7-й: валовая добавленная стоимость и индекс цен промышленной продукции соответственно;

• -    все остальные факторы относятся к неуправляемым, к влиянию окружающей среды на объект.

Затем было исследовано поведение объекта при малых отклонениях управляемых факторов, за счет увеличения и уменьшения значения факторов от 5 до 15 %.

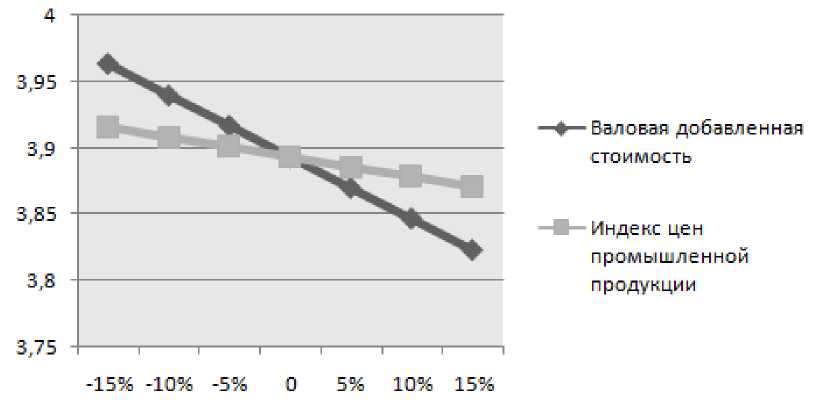
Рис. 4. Развитие объекта при малых отклонениях управляемых факторов

Как видно из диаграммы (рис. 4), при снижении валовой добавленной стоимости на 15%, объем отгруженных товаров собственного производства в сфере добычи полезных ископаемых увеличится 7,1%. Однако увеличение валовой добавленной стоимости на 15% - понизит уровень добычи полезных ископаемых на 9,4%.

При уменьшении на 15 % индекса цен на промышленную продукцию уровень добычи полезных ископаемых повысится на 2,3%, при увеличении на 15% - понизится на 2,3%.

Далее был построен прогноз, показывающий влияние изменений управляемого фактора (при котором достигается наилучший результат поведения объекта при малых отклонениях) на отклонение, возникшее в результате изменения неуправляемого фактора (см. табл. 3).

Таблица 3. Развитие объекта при малом отклонении неуправляемого фактора №2 и малом отклоне- нии управляющего фактора № 5

Факторы		Валовая добавленная стоимость
Л 1 к н & У О д О О н * Я о g я О Щ Q S - И МКН о Ы о ОЙО К Q О « К S о св g щ « Й н о П О о г о у ” S к « о 5S и ю В	От-кло-нения	-15%	-10%	-5%	0%	5%	10%	15%
	-15	3,925	3,902	3,878	3,855	3,832	3,808	3,785
	-10	3,938	3,915	3,891	3,868	3,844	3,821	3,798
	-5	3,951	3,928	3,904	3,881	3,857	3,834	3,81
	0	3,964	3,94	3,917	3,893	3,87	3,847	3,823
	5	3,977	3,953	3,93	3,906	3,883	3,859	3,836
	10	3,989	3,966	3,949	3,919	3,896	3,872	3,849
	15	4,02	3,979	3,955	3,932	3,908	3,885	3,862

Как видно из таблицы 3, наилучшее поведение объекта достигается при понижении валовой добавленной стоимости и увеличении среднегодовой численности работников, находящихся в частной собственности. При выполнении этих условий, возможен подъем уровня развития добычи полезных ископаемых с 3,964 до 4,02, т. е. на 5,6 %.

Проделав аналогичные действия с неуправляемыми факторами 3, 4 получили следующий результат:

• -    при уменьшении среднегодовой численности занятых в экономике и уменьшении валовой добавленной стоимости на 15% достигается увеличение прогноза на 15,6 %;

• -    при увеличении числа действующих предприятий в Пермском крае на 15 % и уменьшении валовой добавленной стоимости на 15 % прогноз увеличится на 4,5 %.

В результате исследования объекта были получены следующие результаты: наибольшее повышение уровня развития добычи полезных ископаемых достигается, при:

• -    снижении валовой добавленной стоимость на 15%;

• -    понижения индекса цен на промышленную продукцию на 15%;

• -    увеличения на 15% среднегодовой численности работников, находящихся в частной собственности;

• -    уменьшения среднегодовой численности занятых в экономике и уменьшения валовой добавленной стоимости на 15%;

• -    увеличения числа действующих предприятий в Пермском крае на 15 %.

Заключение

При выполнении всех вышеизложенных условий значительно уменьшается область отрицательного прогноза, и при этом возможен подъём уровня развития добычи и переработки полезных ископаемых на 9,4%. Все это в большей части зависит от развития экономики в стране. Например, если в стране снизятся цены на промышленную продукцию хотя бы на 5%, то развитие горнодобывающей промышленности в Пермском крае улучшится на 0,39 %. Однако развитие отрицательных тенденций лицо принимающее решение может предотвратить и за счет внедрения новых технологий. С их по- мощью можно сократить затраты на добычу полезных ископаемых, объем реализуемой продукции либо увеличить за счет этого, либо как вариант оставить прежним и не нести убытки.